python求解物理学中的双弹簧质能系统的代码实例

这篇文章主要给大家介绍了关于利用python如何求解物理学中的双弹簧质能系统的相关资料，文中通过示例代码介绍的非常详细，对大家的学习或者工作具有一定的参考学习价值，需要的朋友们下面随着小编来一起学习学习吧。

前言

本文主要给大家介绍了关于利用python求解物理学中双弹簧质能系统的相关内容，分享出来供大家参考学习，下面话不多说了，来一起看看详细的介绍吧。

物理的模型如下：

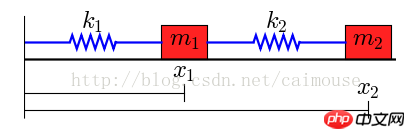
在这个系统里有两个物体，它们的质量分别是m1和m2，被两个弹簧连接在一起，伸缩系统为k1和k2，左端固定。假定没有外力时，两个弹簧的长度为L1和L2。

由于两物体有重力，那么在平面上形成摩擦力，那么摩擦系数分别为b1和b2。所以可以把微分方程写成这样：

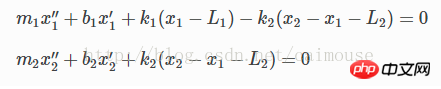
这是一个二阶的微分方程，为了使用python来求解，需要把它转换为一阶微分方程。所以引入下面两个变量：

这两个相当于运动的速度。通过运算可以改为这样：

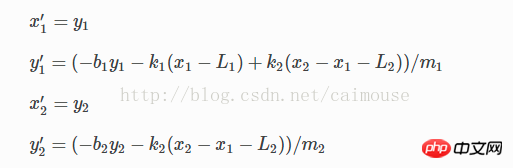
这时可以线性方程改为向量数组的方式，就可以使用python定义了

代码如下：

# Use ODEINT to solve the differential equations defined by the vector field 
from scipy.integrate import odeint 
 
def vectorfield(w, t, p): 
 """ 
 Defines the differential equations for the coupled spring-mass system. 
 
 Arguments: 
  w : vector of the state variables: 
     w = [x1,y1,x2,y2] 
  t : time 
  p : vector of the parameters: 
     p = [m1,m2,k1,k2,L1,L2,b1,b2] 
 """ 
 x1, y1, x2, y2 = w 
 m1, m2, k1, k2, L1, L2, b1, b2 = p 
 
 # Create f = (x1',y1',x2',y2'): 
 f = [y1, 
   (-b1 * y1 - k1 * (x1 - L1) + k2 * (x2 - x1 - L2)) / m1, 
   y2, 
   (-b2 * y2 - k2 * (x2 - x1 - L2)) / m2] 
 return f 
 
# Parameter values 
# Masses: 
m1 = 1.0 
m2 = 1.5 
# Spring constants 
k1 = 8.0 
k2 = 40.0 
# Natural lengths 
L1 = 0.5 
L2 = 1.0 
# Friction coefficients 
b1 = 0.8 
b2 = 0.5 
 
# Initial conditions 
# x1 and x2 are the initial displacements; y1 and y2 are the initial velocities 
x1 = 0.5 
y1 = 0.0 
x2 = 2.25 
y2 = 0.0 
 
# ODE solver parameters 
abserr = 1.0e-8 
relerr = 1.0e-6 
stoptime = 10.0 
numpoints = 250 
 
# Create the time samples for the output of the ODE solver. 
# I use a large number of points, only because I want to make 
# a plot of the solution that looks nice. 
t = [stoptime * float(i) / (numpoints - 1) for i in range(numpoints)] 
 
# Pack up the parameters and initial conditions: 
p = [m1, m2, k1, k2, L1, L2, b1, b2] 
w0 = [x1, y1, x2, y2] 
 
# Call the ODE solver. 
wsol = odeint(vectorfield, w0, t, args=(p,), 
    atol=abserr, rtol=relerr) 
 
with open('two_springs.dat', 'w') as f: 
 # Print & save the solution. 
 for t1, w1 in zip(t, wsol):   
  out = '{0} {1} {2} {3} {4}\n'.format(t1, w1[0], w1[1], w1[2], w1[3]); 
  print(out) 
  f.write(out);

在这里把结果输出到文件two_springs.dat，接着写一个程序来把数据显示成图片，就可以发表论文了，代码如下：

# Plot the solution that was generated 
 
from numpy import loadtxt 
from pylab import figure, plot, xlabel, grid, hold, legend, title, savefig 
from matplotlib.font_manager import FontProperties 
 
t, x1, xy, x2, y2 = loadtxt('two_springs.dat', unpack=True) 
 
figure(1, figsize=(6, 4.5)) 
 
xlabel('t') 
grid(True) 
lw = 1 
 
plot(t, x1, 'b', linewidth=lw) 
plot(t, x2, 'g', linewidth=lw) 
 
legend((r'$x_1$', r'$x_2$'), prop=FontProperties(size=16)) 
title('Mass Displacements for the\nCoupled Spring-Mass System') 
savefig('two_springs.png', dpi=100)

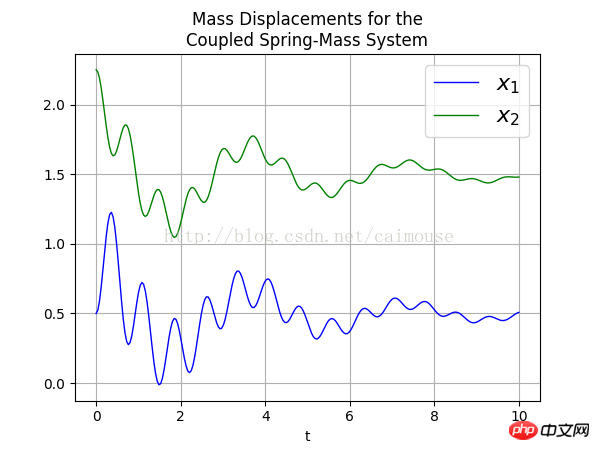
最后来查看一下输出的png图片如下：

总结

以上是python求解物理学中的双弹簧质能系统的代码实例的详细内容。更多信息请关注PHP中文网其他相关文章！