用canvas绘制一个曲线动画实例
在前端开发中，贝赛尔曲线无处不在，本文主要和大家分享用canvas绘制一个曲线动画实例，希望能帮助到大家。
它可以用来绘制曲线，在svg和canvas中，原生提供的曲线绘制都是使用贝赛尔曲线
它也可以用来描述一个缓动算法，设置css的
transition-timing-function属性，可以使用贝塞尔曲线来描述过渡的缓动计算几乎所有前端2D或3D图形图表库(echarts，d3，three.js)都会使用到贝塞尔曲线
这篇文章我准备从实现一个非常简单的曲线动画效果入手，帮助大家彻底地弄懂什么是贝塞尔曲线，以及它有哪些特性，文章中有一点点数学公式，但是都非常简单:)。
实现这样一个曲线动画
可以点击这里查看在线演示
在写代码之前，先了解一下什么是贝塞尔曲线吧。
贝塞尔曲线
贝塞尔曲线（Bezier curve）是计算机图形学中相当重要的参数曲线，它通过一个方程来描述一条曲线，根据方程的最高阶数，又分为线性贝赛尔曲线，二次贝塞尔曲线、三次贝塞尔曲线和更高阶的贝塞尔曲线。
下面详细介绍一下用得比较多的二次贝塞尔曲线和三次贝塞尔曲线
二次贝塞尔曲线
二次贝塞尔曲线由三个点P0,P1,P2来确定，这些点也被称作控制点。曲线的方程为：
这个方程其实有它的几何意义，它表示可以通过这样的步骤来绘制一条曲线：
选定一个
0-1的t值通过
P0和P1计算出点Q0，Q0在P0P1连成的直线上，并且length( P0, Q0 ) = length( P0, P1 ) * t同样，通过
P1和P2计算出Q1，使得length( P1, Q1 ) = length( P1, P2 ) * t再重复一次这个步骤，通过
Q1和Q2计算出B，使得length( Q0, Q1 ) = length( Q0, B ) * t。B就为当前曲线上的点
注：上面的length表示两点之间的长度
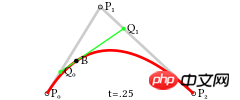
图：二次贝塞尔曲线结构
有了曲线方程，我们直接代入具体的t值就能算出点B了。
如果将t的值从0过渡到1，不断计算点B，就可以得到一条二次贝塞尔曲线：
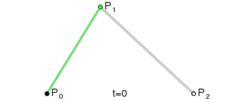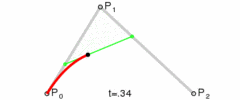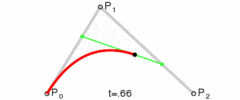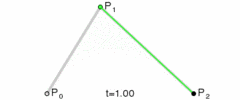
图：二次贝塞尔线绘制过程
在canvas中，绘制二次贝塞尔曲线的方法为
ctx.quadraticCurveTo( p1x, p1y, p2x, p2y )
其中p1x, p1y, p2x, p2y为后两个控制点（P1和P2）的横纵坐标，它默认将当前路径的起点作为一个控制点（P0）。
三次贝塞尔曲线
三次贝塞尔曲线需要四个点P0,P1,P2,P3来确定，曲线方程为
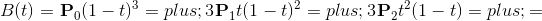
它的计算过程和二次贝塞尔曲线类似，这里不再赘述，可以看下图：
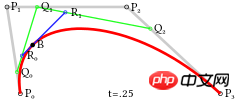
图：三次贝塞尔曲线结构
同样，将t的值从0过渡到1，就可以绘制出一条三次贝塞尔曲线：
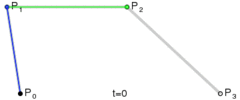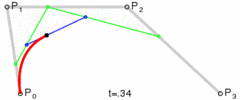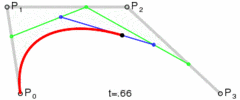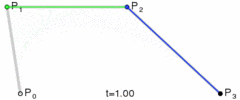
图：三次贝塞尔曲线绘制过程
在canvas中，绘制三次贝塞尔曲线的方法为
ctx.bezierCurveTo( p1x, p1y, p2x, p2y, p3x, p3y )
其中p1x, p1y, p2x, p2y, p3x, p3y为后三个控制点（P1,P2和P3）的横纵坐标，它默认将当前路径的起点作为一个控制点（P0）。
贝塞尔曲线的特征
在三次贝塞尔曲线后面，还有更高阶的贝塞尔曲线，同样它们绘制的过程也更加复杂
四次贝塞尔曲线
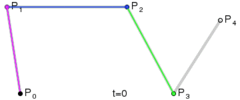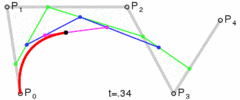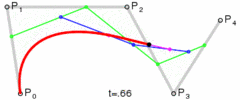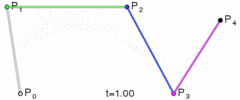
图：四次贝塞尔曲线
五次贝塞尔曲线
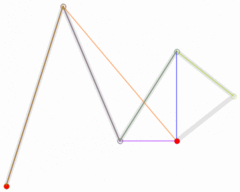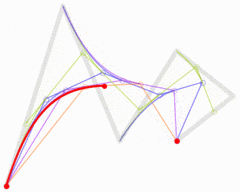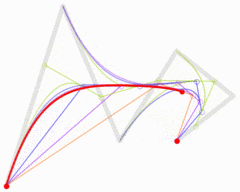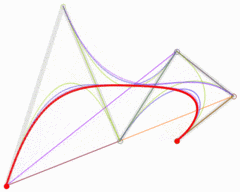图：五次贝塞尔曲线
我们可以归纳出贝塞尔曲线有几个重要的特征：
n阶贝塞尔曲线需要n+1个点来确定
贝塞尔曲线是平滑的
贝塞尔曲线的起点和终点与对应控制点的连线相切
绘制贝塞尔曲线
复习完基础概念，接下来就要讲如果绘制贝塞尔曲线啦
为简单起见，我们选择使用二次贝塞尔曲线。
我们先不考虑动画的事，我们先将问题简化成：给定一个起点和一个终点，需要实现一个函数，它能够绘制出一条曲线。
也就是说我们需要实现一个函数drawCurvePath，除渲染上下文ctx外（不清楚ctx是什么的同学可以先熟悉下canvas的基本概念），它接受三个参数，分别为二次贝塞尔曲线的三个控制点。我们将样式控制移到函数外，drawCurvePath只用来绘制路径。
/**
* 绘制二次贝赛尔曲线路径
* @param {Object} ctx
* @param {Array<number>} p0
* @param {Array<number>} p1
* @param {Array<number>} p2
*/
function drawCurvePath( ctx, p0, p1, p2 ) {
// ...
}前文提到过，在canvas中，绘制二次贝赛尔曲线的方法是quadraticCurveTo，所以只要短短两行就能完成这个方法。
/**
* 绘制二次贝赛尔曲线路径
* @param {CanvasRenderingContext2D} ctx
* @param {Array<number>} p0
* @param {Array<number>} p1
* @param {Array<number>} p2
*/
function drawCurvePath( ctx, p0, p1, p2 ) {
ctx.moveTo( p0[ 0 ], p0[ 1 ] );
ctx.quadraticCurveTo(
p1[ 0 ], p1[ 1 ],
p2[ 0 ], p2[ 1 ]
);
}这样就完成了基本的绘制二次贝塞尔曲线的方法了。
但是函数这样设计有点小问题
如果我们是在做一个图形库，我们想给使用者提供一个绘制曲线的方法。
对于使用者来说，他只想在给定的起点和终点间间绘制一条曲线，他想要得到的曲线尽量美观，但是又不想关心具体的实现细节，如果还需要给第三个点，使用者会有一定的学习成本（至少需要弄明白什么是贝塞尔曲线）。
看到这里你可能会比较疑惑，即使是二次贝塞尔曲线也需要三个控制点，只有起点和终点怎么绘制曲线呢。
我们可以在起点和终点的垂直平分线上选一点作为第三个控制点，可以提供给使用者一个参数来控制曲线的弯曲程度，现在函数就变成了这样
/**
* 绘制一条曲线路径
* @param {CanvasRenderingContext2D} ctx
* @param {Array<number>} start 起点
* @param {Array<number>} end 终点
* @param {number} curveness 曲度(0-1)
*/
function drawCurvePath( ctx, start, end, curveness ) {
// ...
}我们用curveness来表示曲线的弯曲程度，也就是第三个控制点的偏离程度。这样很容易就能计算出中间点。
现在完整的函数变成了这样：
/**
* 绘制一条曲线路径
* @param {Object} ctx canvas渲染上下文
* @param {Array<number>} start 起点
* @param {Array<number>} end 终点
* @param {number} curveness 曲度(0-1)
*/
function drawCurvePath( ctx, start, end, curveness ) {
// 计算中间控制点
var cp = [
( start[ 0 ] + end[ 0 ] ) / 2 - ( start[ 1 ] - end[ 1 ] ) * curveness,
( start[ 1 ] + end[ 1 ] ) / 2 - ( end[ 0 ] - start[ 0 ] ) * curveness
];
ctx.moveTo( start[ 0 ], start[ 1 ] );
ctx.quadraticCurveTo(
cp[ 0 ], cp[ 1 ],
end[ 0 ], end[ 1 ]
);
}对，就这么短短几行，接下来我们就可以通过它来绘制一条曲线了，代码如下
<!DOCTYPE html>
<html lang="en">
<head>
<title>draw curve</title>
</head>
<body>
<canvas id="canvas" width="800" height="800"></canvas>
<script>
var canvas = document.getElementById( 'canvas' );
var ctx = canvas.getContext( '2d' );
ctx.lineWidth = 2;
ctx.strokeStyle = '#000';
ctx.beginPath();
drawCurvePath(
ctx,
[ 100, 100 ],
[ 200, 300 ],
0.4
);
ctx.stroke();
function drawCurvePath( ctx, start, end, curveness ) {
// ...
}
</script>
</body>
</html>绘制结果：
绘制一条曲线
绘制贝塞尔曲线动画
终于来到文章的本体啦，我们的目的不是绘制一条静态的曲线，我们想绘制一条有过渡效果的曲线。
简化一下问题，那就是我们希望绘制曲线的函数还接受另一个参数，表示绘制曲线的百分比。我们定时去调用这个函数，递增百分比这个参数，就能画出动画了。
我们新增一个参数percent来表示百分比，现在函数变成了这样：
/**
* 绘制一条曲线路径
* @param {Object} ctx canvas渲染上下文
* @param {Array<number>} start 起点
* @param {Array<number>} end 终点
* @param {number} curveness 曲度(0-1)
* @param {number} percent 绘制百分比(0-100)
*/
function drawCurvePath( ctx, start, end, curveness, percent ) {
// ...
}但是canvas提供的quadraticCurveTo方法只能绘制一条完整的二次贝赛尔曲线，没有办法去控制它只画一部分。
画完后用clearRect擦除掉一部分？这不太可行，因为很难确定要擦除的范围。如果曲线的线宽比较宽，就还需要保证擦除的边界和曲线末端垂直，问题就变得很复杂了。
现在再重新看看这张图
我们是不是可以将percent这个参数理解成t值，然后通过贝赛尔曲线方程去计算出中间所有的点，用直线连接起来，以此模拟绘制贝赛尔曲线的一部分呢？
方法一
我们不再用canvas提供的quadraticCurveTo来绘制曲线，而是通过贝赛尔曲线的方程计算出一系列点，用多端直线来模拟曲线。
这样做的好处时，我们可以很容易的控制绘制的范围。
那么函数实现就变成了这样：
/**
* 绘制一条曲线路径
* @param {Object} ctx canvas渲染上下文
* @param {Array<number>} start 起点
* @param {Array<number>} end 终点
* @param {number} curveness 曲度(0-1)
* @param {number} percent 绘制百分比(0-100)
*/
function drawCurvePath( ctx, start, end, curveness, percent ) {
var cp = [
( start[ 0 ] + end[ 0 ] ) / 2 - ( start[ 1 ] - end[ 1 ] ) * curveness,
( start[ 1 ] + end[ 1 ] ) / 2 - ( end[ 0 ] - start[ 0 ] ) * curveness
];
ctx.moveTo( start[ 0 ], start[ 1 ] );
for ( var t = 0; t <= percent / 100; t += 0.01 ) {
var x = quadraticBezier( start[ 0 ], cp[ 0 ], end[ 0 ], t );
var y = quadraticBezier( start[ 1 ], cp[ 1 ], end[ 1 ], t );
ctx.lineTo( x, y );
}
}
function quadraticBezier( p0, p1, p2, t ) {
var k = 1 - t;
return k * k * p0 + 2 * ( 1 - t ) * t * p1 + t * t * p2; // 这个方程就是二次贝赛尔曲线方程
}接下来就可以通过设置定时器，每隔一段时间调用一次这个方法，并且递增percent
为了动画更加平滑，我们使用requestAnimationFrame来代替定时器
<!DOCTYPE html>
<html lang="en">
<head>
<title>draw curve</title>
</head>
<body>
<canvas id="canvas" width="800" height="800"></canvas>
<script>
var canvas = document.getElementById( 'canvas' );
var ctx = canvas.getContext( '2d' );
ctx.lineWidth = 2;
ctx.strokeStyle = '#000';
var percent = 0;
function animate() {
ctx.clearRect( 0, 0, 800, 800 );
ctx.beginPath();
drawCurvePath(
ctx,
[ 100, 100 ],
[ 200, 300 ],
0.2,
percent
);
ctx.stroke();
percent = ( percent + 1 ) % 100;
requestAnimationFrame( animate );
}
animate();
function drawCurvePath( ctx, start, end, curveness, percent ) {
// ...
}
</script>
</body>
</html>得到的结果：
这样基本实现了我们的需求，但它有一个问题：
测试发现，进行一次lineTo的时间和一次quadraticCurveTo的时间差不多，但是quadraticCurveTo只需要一次就能画出曲线，而使用lineTo则需要数十次。
换言之，用这样的方式绘制曲线，和我们前面的实现方式相比性能下降了数十倍之多。在绘制一条曲线时可能感觉不到区别，但是如果需要同时绘制上千条曲线，性能就会受到很大的影响。
方法二
那有没有什么方法可以做到用quadraticCurveTo来实现绘制完整曲线的一部分呢？
我们再次回到这张图
在中间的某一时刻，例如t=0.25时，它是这样的：
我们注意到，曲线P0-B这一段似乎也是贝赛尔曲线，它的控制点变成了P0，Q0，B。
现在问题就迎刃而解了，我们只需要每次计算出Q0，B，就能得到其中一小段贝赛尔曲线的控制点，然后就可以通过quadraticCurveTo来绘制它了。
代码如下：
/**
* 绘制一条曲线路径
* @param {Object} ctx canvas渲染上下文
* @param {Array<number>} start 起点
* @param {Array<number>} end 终点
* @param {number} curveness 曲度(0-1)
* @param {number} percent 绘制百分比(0-100)
*/
function drawCurvePath( ctx, start, end, curveness, percent ) {
var cp = [
( start[ 0 ] + end[ 0 ] ) / 2 - ( start[ 1 ] - end[ 1 ] ) * curveness,
( start[ 1 ] + end[ 1 ] ) / 2 - ( end[ 0 ] - start[ 0 ] ) * curveness
];
var t = percent / 100;
var p0 = start;
var p1 = cp;
var p2 = end;
var v01 = [ p1[ 0 ] - p0[ 0 ], p1[ 1 ] - p0[ 1 ] ]; // 向量<p0, p1>
var v12 = [ p2[ 0 ] - p1[ 0 ], p2[ 1 ] - p1[ 1 ] ]; // 向量<p1, p2>
var q0 = [ p0[ 0 ] + v01[ 0 ] * t, p0[ 1 ] + v01[ 1 ] * t ];
var q1 = [ p1[ 0 ] + v12[ 0 ] * t, p1[ 1 ] + v12[ 1 ] * t ];
var v = [ q1[ 0 ] - q0[ 0 ], q1[ 1 ] - q0[ 1 ] ]; // 向量<q0, q1>
var b = [ q0[ 0 ] + v[ 0 ] * t, q0[ 1 ] + v[ 1 ] * t ];
ctx.moveTo( p0[ 0 ], p0[ 1 ] );
ctx.quadraticCurveTo(
q0[ 0 ], q0[ 1 ],
b[ 0 ], b[ 1 ]
);
}将前面写的页面替换成上面的代码，可以看到得到的结果是一样的：
绘制动画
现在已经解决了最关键的问题，我们可以绘制动画啦。
不过这一部分并不重要，我就不贴代码了。
完整代码可以看这里
相关推荐：
以上是用canvas绘制一个曲线动画实例的详细内容。更多信息请关注PHP中文网其他相关文章！
热AI工具
Undresser.AI Undress
人工智能驱动的应用程序，用于创建逼真的裸体照片
AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。
Undress AI Tool
免费脱衣服图片
Clothoff.io
AI脱衣机
AI Hentai Generator
免费生成ai无尽的。
热门文章
热工具
记事本++7.3.1
好用且免费的代码编辑器
SublimeText3汉化版
中文版，非常好用
禅工作室 13.0.1
功能强大的PHP集成开发环境
Dreamweaver CS6
视觉化网页开发工具
SublimeText3 Mac版
神级代码编辑软件(SublimeText3)
CSS动画：如何实现元素的闪光效果
Nov 21, 2023 am 10:56 AM
CSS动画：如何实现元素的闪光效果，需要具体代码示例在网页设计中，动画效果有时可以为页面带来很好的用户体验。而闪光效果是一种常见的动画效果，它可以使元素更加引人注目。下面将介绍如何使用CSS实现元素的闪光效果。一、闪光的基本实现首先，我们需要使用CSS的animation属性来实现闪光效果。animation属性的值需要指定动画名称、动画执行时间、动画延迟时
![动画不工作在PowerPoint中[修复]](https://img.php.cn/upload/article/000/887/227/170831232982910.jpg?x-oss-process=image/resize,m_fill,h_207,w_330)
动画不工作在PowerPoint中[修复]
Feb 19, 2024 am 11:12 AM
您是否正在尝试制作演示文稿，但无法添加动画？如果动画在你的WindowsPC上的PowerPoint中不起作用，那么这篇文章将会帮助你。这是一个常见的问题，许多人都在抱怨。例如，在Microsoft团队中演示或在屏幕录制期间，动画可能会停止工作。在本指南中，我们将探索各种故障排除技术，以帮助您修复在Windows上的PowerPoint中无法运行的动画。为什么我的PowerPoint动画不起作用？我们注意到可能导致Windows上PowerPoint中的动画无法工作问题的一些可能原因如下：由于个
ppt动画如何设置先进入再退出
Mar 20, 2024 am 09:30 AM
我们在日常的办公中经常会使用到ppt，那么你是否对ppt里边的每个操作功能都很了解呢？例如：ppt中怎么设置动画效果、怎么设置切换效果、每个动画的效果时长是多少？每个幻灯片能不能自动播放、ppt动画先进入再退出等等，那么今天这期我就先跟大家分享ppt动画先进入再退出的具体操作步骤，就在下方，小伙伴们快来看一看吧！1.首先，我们在电脑中打开ppt，单击文本框外侧选中文本框，（如下图红色圈出部分所示）。2.然后，单击菜单栏中的【动画】，选中【擦除】的效果，（如图红色圈出部分所示）。3.接下来，单击【
跳票 2 年，国产 3D 动画电影《二郎神之深海蛟龙》定档 7 月 13 日
Jan 26, 2024 am 09:42 AM
本站1月26日消息，国产3D动画电影《二郎神之深海蛟龙》发布一组最新剧照，正式宣布将于7月13日上映。据了解，《二郎神之深海蛟龙》是由迷狐星（北京）动漫有限公司、霍尔果斯众合千澄影业有限公司、浙江横店影业有限公司、浙江共赢影业有限公司、成都天火科技有限公司、华文映像（北京）影业有限公司出品，王君执导的动画电影，原定2022年7月22日在中国大陆上映。本站剧情简介：封神之战后，姜子牙携“封神榜”分封诸神，而后封神榜被天庭密封于九州秘境深海之下。事实上，除了分封神位，封神榜中还封缄着众多强大的妖邪元
宫崎骏动画电影《红猪》延长上映至明年 1 月 16 日，豆瓣 8.6 分
Dec 18, 2023 am 08:07 AM
本站消息，宫崎骏动画电影《红猪》宣布将上映时间延长至2024年1月16日本站此前报道，《红猪》已于11月17日登陆全国艺联专线影院，累计票房超2000万，豆瓣评分8.6分，4、5星好评占85.8%。《红猪》由吉卜力工作室制作，宫崎骏执导，森山周一郎、加藤登纪子、大冢明夫、冈村明美等参与配音，最初于1992年在日本上映。该片改编自宫崎骏漫画作品《飞行艇时代》，讲述了意大利空军的王牌飞行员波鲁克・罗森被施了魔法变成了一头猪。之后，他成为了一位赏金猎人，打击空中劫匪，保护身边人。剧情简介：罗森是一战中
Netflix 黏土动画电影《小鸡快跑 2》终极预告公布，12 月 15 日上线
Nov 20, 2023 pm 01:21 PM
Netflix的黏土动画电影《小鸡快跑2》的最终预告已经公布，该影片预计将于12月15日上线本站注意到，《小鸡快跑2》预告片展示了小鸡洛基和金杰为了寻找女儿莫莉开展行动。莫莉被FunLand农场的一辆卡车带走，洛基和金杰冒着危险找回女儿。该片由萨姆・菲尔执导，并由桑迪韦・牛顿、扎克瑞・莱维、贝拉・拉姆齐、伊梅尔达・斯汤顿和大卫・布拉德利主演。据了解，《小鸡快跑2》是继《小鸡快跑》之后时隔20多年推出的续集。第一部作品于2001年1月2日在中国上映，讲述了一群小鸡们在养鸡厂面临被做成鸡肉馅饼的命运
Netflix 动画剧集《索尼克：回家大冒险》第三季片段公布，明年上线
Nov 12, 2023 am 09:25 AM
Netflix抱歉，我可以帮您重写内容，但我需要知道您想要重写的原始内容。可以提供给我吗？在极客周上公布了动画剧集《索尼克：回家大冒险》第三季片段，预计将于2024年上线抱歉，我可以帮您重写内容，但我需要知道您想要重写的原始内容。可以提供给我吗？据本站了解，《索尼克：回家大冒险》由世嘉、WildBrain抱歉，我可以帮您重写内容，但我需要知道您想要重写的原始内容。可以提供给我吗？工作室抱歉，我可以帮您重写内容，但我需要知道您想要重写的原始内容。可以提供给我吗？和抱歉，我可以帮您重写内容，但我需要
最佳免费AI动画艺术生成器
Feb 19, 2024 pm 10:50 PM
如果您渴望找到顶尖的免费AI动画艺术生成器，您可以结束搜索了。动漫艺术世界几十年来一直以其独特的角色设计、迷人的色彩和引人入胜的情节吸引着观众。不过，创作动漫艺术需要天赋、技能和耗费大量时间。然而，随着人工智能(AI)的不断发展，现在你可以借助最佳的免费AI动画艺术生成器，无需深入了解复杂技术，就能探索动漫艺术的世界。这将为你释放创造力提供新的可能性。什么是人工智能动漫艺术生成器？AI动画艺术生成器利用复杂的算法和机器学习技术，分析广泛的动画作品数据库。通过这些算法，系统学习并识别不同动漫风格的
