php实现几种常见的排序算法-php教程-PHP中文网

首页

后端开发

php教程

php实现几种常见的排序算法

小云云

Mar 10, 2018 pm 01:34 PM

php 排序算法

交换排序：交换排序的基本思想是，比较两个记录键值的大小，如果这两个记录键值的大小出现逆序，则交换这两个记录，这样将键值较小的记录向序列前部移动，键值较大的记录向序列后部移动。

一、冒泡排序

介绍：

冒泡排序（Bubble Sort，台湾译为：泡沫排序或气泡排序）是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

步骤：

比较相邻的元素。如果第一个比第二个大，就交换他们两个。
对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。
针对所有的元素重复以上的步骤，除了最后一个。
持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

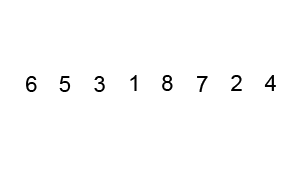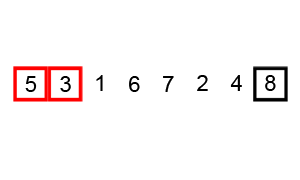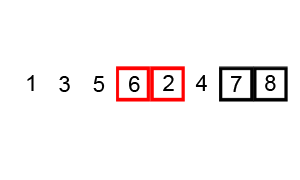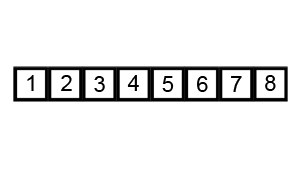
冒泡排序理解起来是最简单，但是时间复杂度（O(n^2)）也是最大的之一，实现代码如下：

<br/>

登录后复制

$arr=array(1,43,54,62,21,66,32,78,36,76,39);
function getpao($arr)
{
$len=count($arr);
//设置一个空数组用来接收冒出来的泡
//该层循环控制需要冒泡的轮数
for($i=1;$i<$len;$i++)
{ //该层循环用来控制每轮冒出一个数需要比较的次数
for($k=0;$k<$len-$i;$k++)
{
if($arr[$k]>$arr[$k+1])
{
$tmp=$arr[$k+1];
$arr[$k+1]=$arr[$k];
$arr[$k]=$tmp;
}
}
}
return $arr;
}

二、快速排序

介绍：

快速排序是由东尼·霍尔所发展的一种排序算法。在平均状况下，排序 n 个项目要Ο(n log n)次比较。在最坏状况下则需要Ο(n2)次比较，但这种状况并不常见。事实上，快速排序通常明显比其他Ο(n log n) 算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地被实现出来，且在大部分真实世界的数据，可以决定设计的选择，减少所需时间的二次方项之可能性。

步骤：

从数列中挑出一个元素，称为 “基准”（pivot），
重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

快排也是一个高效的排序算法，它的时间复杂度也是O(nlogn)。代码如下：

function quick_sort($arr) {
//先判断是否需要继续进行
$length = count($arr);
if($length <= 1) {
return $arr;
}
//如果没有返回，说明数组内的元素个数多余1个，需要排序
//选择一个标尺
//选择第一个元素
$base_num = $arr[0];
//遍历除了标尺外的所有元素，按照大小关系放入两个数组内
//初始化两个数组
$left_array = array();//小于标尺的
$right_array = array();//大于标尺的
for($i=1; $i<$length; $i++) {
if($base_num > $arr[$i]) {
//放入左边数组
$left_array[] = $arr[$i];
} else {
//放入右边
$right_array[] = $arr[$i];
}
}
//再分别对左边和右边的数组进行相同的排序处理方式
//递归调用这个函数,并记录结果
$left_array = quick_sort($left_array);
$right_array = quick_sort($right_array);
//合并左边标尺右边
return array_merge($left_array, array($base_num), $right_array);
}

选择排序

选择排序包括两种，分别是直接选择排序和堆排序，选择排序的基本思想是每一次在n-i+1（i=1,2,3，...，n-1）个记录中选取键值最小的记录作为有序序列的第i个记录

三、选择排序

介绍：

选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小元素，然后放到排序序列末尾。以此类推，直到所有元素均排序完毕。

选择排序理解起来也比较简单，时间复杂度也是O(n^2)，实现代码如下：

<br/>

登录后复制

[php] view plain copy

function select_sort($arr) {
//实现思路双重循环完成，外层控制轮数，当前的最小值。内层控制的比较次数
//$i 当前最小值的位置，需要参与比较的元素
for($i=0, $len=count($arr); $i<$len-1; $i++) {
//先假设最小的值的位置
$p = $i;
//$j 当前都需要和哪些元素比较，$i 后边的。
for($j=$i+1; $j<$len; $j++) {
//$arr[$p] 是当前已知的最小值
if($arr[$p] > $arr[$j]) {
//比较，发现更小的,记录下最小值的位置；并且在下次比较时，
// 应该采用已知的最小值进行比较。
$p = $j;
}
}
//已经确定了当前的最小值的位置，保存到$p中。
//如果发现最小值的位置与当前假设的位置$i不同，则位置互换即可
if($p != $i) {
$tmp = $arr[$p];
$arr[$p] = $arr[$i];
$arr[$i] = $tmp;
}
}
//返回最终结果
return $arr;
}

四、堆排序

介绍：

堆积排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

步骤：

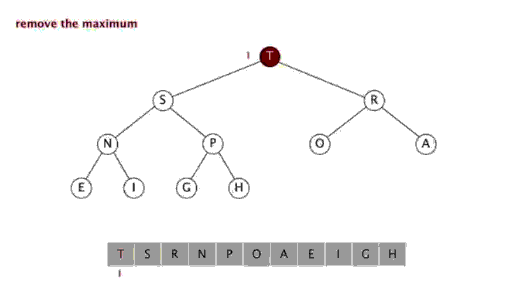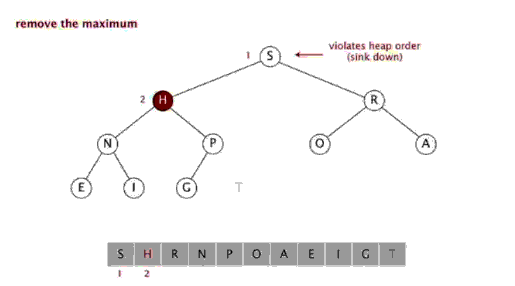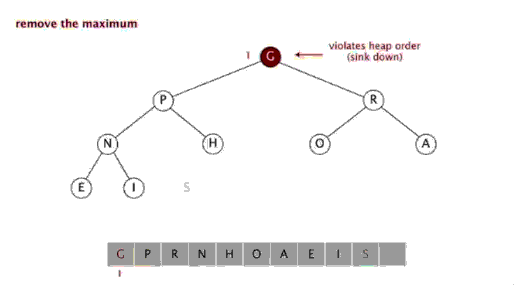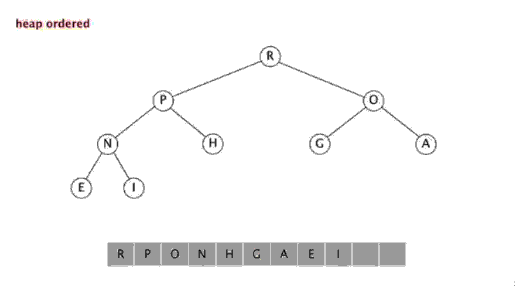
堆排序是指利用堆积树（堆）这种数据结构所设计的一种排序算法，利用数组的特点快速定位指定索引的元素。堆分为大根堆和小根堆，是完全二叉树。大根堆的要求是每个节点的值都不大于其父节点的值，即A[PARENT[i]] >= A[i]。在数组的非降序排序中，需要使用的就是大根堆，因为根据大根堆的要求可知，最大的值一定在堆顶。

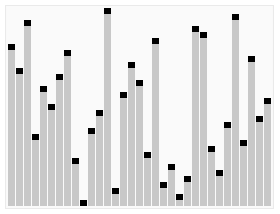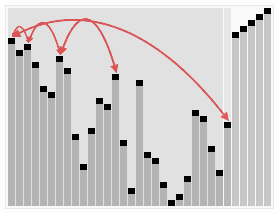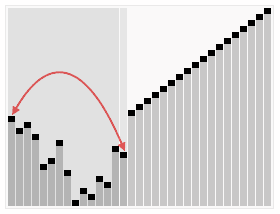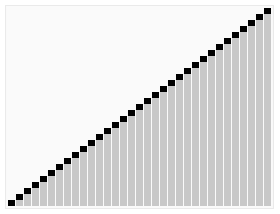
排序效果：

堆排序是一种高效的排序算法，它的时间复杂度是O(nlogn)。原理是：先把数组转为一个最大堆，然后把第一个元素跟第i元素交换，然后把剩下的i-1个元素转为最大堆，然后再把第一个元素与第i-1个元素交换，以此类推。实现代码如下：

function heapSort($arr) {
    $len = count($arr);    // 先建立最大堆
    for ($i = floor(($len - 1) / 2); $i >= 0; $i--) {        $s = $i;        $childIndex = $s * 2 + 1;        while ($childIndex < $len) {            // 在父、左子、右子中 ，找到最大的
            if ($childIndex + 1 < $len && $arr[$childIndex] < $arr[$childIndex + 1]) $childIndex++;            if ($arr[$s] < $arr[$childIndex]) {                $t = $arr[$s];                $arr[$s] = $arr[$childIndex];                $arr[$childIndex] = $t;                $s = $childIndex;                $childIndex = $childIndex * 2 + 1;
            } else {                break;
            }
        }
    }    // 从最后一个元素开始调整
    for ($i = $len - 1; $i > 0; $i--) {        $t = $arr[$i];        $arr[$i] = $arr[0];        $arr[0] = $t;        // 调整第一个元素
        $s = 0;        $childIndex = 1;        while ($childIndex < $i) {            // 在父、左子、右子中 ，找到最大的
            if ($childIndex + 1 < $i && $arr[$childIndex] < $arr[$childIndex + 1]) $childIndex++;            if ($arr[$s] < $arr[$childIndex]) {                $t = $arr[$s];                $arr[$s] = $arr[$childIndex];                $arr[$childIndex] = $t;                $s = $childIndex;                $childIndex = $childIndex * 2 + 1;
            } else {                break;
            }
        }
    }    return $arr;
}$arr = [3,1,13,5,7,11,2,4,14,9,15,6,12,10,8];
print_r(bubbleSort($arr));

登录后复制

插入排序

五、插入排序

介绍：

插入排序（Insertion Sort）的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

步骤：

从第一个元素开始，该元素可以认为已经被排序
取出下一个元素，在已经排序的元素序列中从后向前扫描
如果该元素（已排序）大于新元素，将该元素移到下一位置
重复步骤3，直到找到已排序的元素小于或者等于新元素的位置
将新元素插入到该位置中
重复步骤2

感觉插入排序跟冒泡排序有点相似，时间复杂度也是O(n^2)，实现代码如下：

[php] view plain copy

function insert_sort($arr) {
//区分哪部分是已经排序好的
//哪部分是没有排序的
//找到其中一个需要排序的元素
//这个元素就是从第二个元素开始，到最后一个元素都是这个需要排序的元素
//利用循环就可以标志出来
//i循环控制每次需要插入的元素，一旦需要插入的元素控制好了，
//间接已经将数组分成了2部分，下标小于当前的（左边的），是排序好的序列
for($i=1, $len=count($arr); $i<$len; $i++) {
//获得当前需要比较的元素值。
$tmp = $arr[$i];
//内层循环控制比较并插入
for($j=$i-1;$j>=0;$j--) {
//$arr[$i];//需要插入的元素; $arr[$j];//需要比较的元素
if($tmp < $arr[$j]) {
//发现插入的元素要小，交换位置
//将后边的元素与前面的元素互换
$arr[$j+1] = $arr[$j];
//将前面的数设置为当前需要交换的数
$arr[$j] = $tmp;
} else {
//如果碰到不需要移动的元素
//由于是已经排序好是数组，则前面的就不需要再次比较了。
break;
}
}
}
//将这个元素插入到已经排序好的序列内。
//返回
return $arr;
}

<br/>

登录后复制

六、希尔排序

介绍：

希尔排序，也称递减增量排序算法，是插入排序的一种高速而稳定的改进版本。

希尔排序是基于插入排序的以下两点性质而提出改进方法的：

1、插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率

2、但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位>

排序效果：

希尔排序其实可以理解是插入排序的一个优化版，它的效率跟增量有关，增量要取多少，根据不同的数组是不同的，所以希尔排序是一个不稳定的排序算法，它的时间复杂度为O(nlogn)到O(n^2)之间，实现代码如下：

function shellSort($arr) {
    $len = count($arr);    $stepSize = floor($len / 2);    while ($stepSize >= 1) {        for ($i = $stepSize; $i < $len; $i++) {            if ($arr[$i] < $arr[$i - $stepSize]) {                $t = $arr[$i];                $j = $i - $stepSize;                while ($j >= 0 && $t < $arr[$j]) {                    $arr[$j + $stepSize] = $arr[$j];                    $j -= $stepSize;
                }                $arr[$j + $stepSize] = $t;
            }
        }        // 缩小步长，再进行插入排序
        $stepSize = floor($stepSize / 2);
    }    return $arr;
}$arr = [3,1,13,5,7,11,2,4,14,9,15,6,12,10,8];
print_r(bubbleSort($arr));

登录后复制

七、归并排序

介绍：

归并排序（Merge sort，台湾译作：合并排序）是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（pide and Conquer）的一个非常典型的应用

步骤：

申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
设定两个指针，最初位置分别为两个已经排序序列的起始位置
比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
重复步骤3直到某一指针达到序列尾
将另一序列剩下的所有元素直接复制到合并序列尾

排序效果：

归并排序的时间复杂度也是O(nlogn)。原理是：对于两个排序好的数组，分别遍历这两个数组，获取较小的元素插入新的数组中，那么，这么新的数组也会是排序好的。代码如下：

我们先来看看主函数部分：

//交换函数function swap(array &$arr,$a,$b){
    $temp = $arr[$a];    $arr[$a] = $arr[$b];    $arr[$b] = $temp;
}//归并算法总函数function MergeSort(array &$arr){
    $start = 0;    $end = count($arr) - 1;
    MSort($arr,$start,$end);
}

登录后复制

在总函数中，我们只调用了一个 MSort() 函数，因为我们要使用递归调用，所以将 MSort() 封装起来。

下面我们来看看 MSort() 函数：

function MSort(array &$arr,$start,$end){    //当子序列长度为1时，$start == $end，不用再分组    if($start < $end){        $mid = floor(($start + $end) / 2);	//将 $arr 平分为 $arr[$start - $mid] 和 $arr[$mid+1 - $end]        MSort($arr,$start,$mid);			//将 $arr[$start - $mid] 归并为有序的$arr[$start - $mid]        MSort($arr,$mid + 1,$end);			//将 $arr[$mid+1 - $end] 归并为有序的 $arr[$mid+1 - $end]        Merge($arr,$start,$mid,$end);       //将$arr[$start - $mid]部分和$arr[$mid+1 - $end]部分合并起来成为有序的$arr[$start - $end]
    }
}

登录后复制

上面的 MSort() 函数实现将数组分半再分半（直到子序列长度为1），然后将子序列合并起来。

现在是我们的归并操作函数 Merge() :

//归并操作function Merge(array &$arr,$start,$mid,$end){
    $i = $start;    $j=$mid + 1;    $k = $start;    $temparr = array();    while($i!=$mid+1 && $j!=$end+1)
    {       if($arr[$i] >= $arr[$j]){           $temparr[$k++] = $arr[$j++];
       }       else{           $temparr[$k++] = $arr[$i++];
       }
    }    //将第一个子序列的剩余部分添加到已经排好序的 $temparr 数组中
    while($i != $mid+1){        $temparr[$k++] = $arr[$i++];
    }    //将第二个子序列的剩余部分添加到已经排好序的 $temparr 数组中
    while($j != $end+1){        $temparr[$k++] = $arr[$j++];
    }    for($i=$start; $i<=$end; $i++){        $arr[$i] = $temparr[$i];
    }
}

登录后复制

到了这里，我们的归并算法就完了。我们调用试试：

$arr = array(9,1,5,8,3,7,4,6,2);
MergeSort($arr);
var_dump($arr);

登录后复制

热AI工具

热工具

php实现几种常见的排序算法

热AI工具

Undresser.AI Undress

AI Clothes Remover

Undress AI Tool

Clothoff.io

Video Face Swap

热门文章

热工具

记事本++7.3.1

SublimeText3汉化版

禅工作室 13.0.1

Dreamweaver CS6

SublimeText3 Mac版

热门话题