php堆排序详解

 堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素。堆分为大根堆和小根堆，是完全二叉树。大根堆的要求是每个节点的值都不大于其父节点的值，即A[PARENT[i]] >= A[i]。在数组的非降序排序中，需要使用的就是大根堆，因为根据大根堆的要求可知，最大的值一定在堆顶。

堆的定义

    一个完全二叉树中，任意父结点总是大于或等于（小于或等于）任何一个子节点，则为大顶堆（小顶堆）。

堆的数组存储方式

完全二叉树适合采用顺序存储的方式，因此一个数组可以看成一个完全二叉树。

• 节点编号：树根起，自上层到下层，每层从左至右，给所有结点顺序编号，能得到一个反映整个二叉树结构的线性序列。

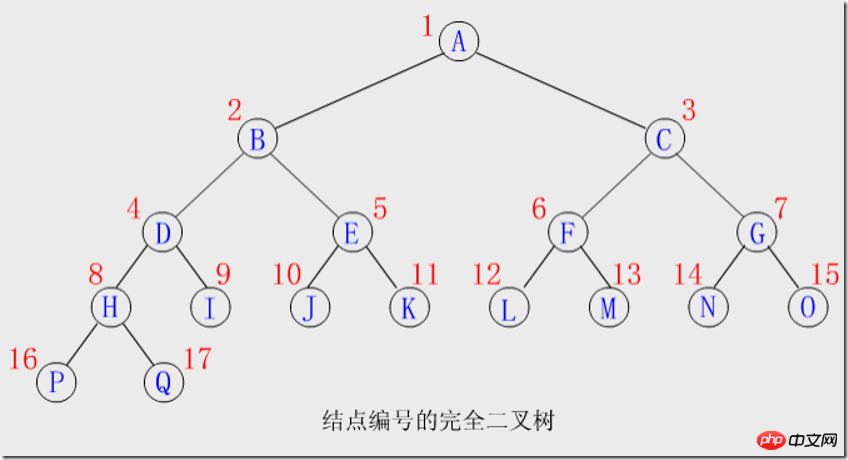
• 编号特点：

从一个结点的编号就可推得其双亲，左、右孩子，兄弟等结点的编号。假设编号为i的结点是ki(1≤i≤n)，则有：

　　①若i>1，则ki的双亲编号为i/2；若i=1，则Ki是根结点，无双亲。

　　②若2i≤n，则Ki的左孩子的编号是2i；否则，Ki无左孩子，即Ki必定是叶子。因此完全二叉树中编号i>n/2的结点必定是叶结点。

　　③若2i+1≤n，则Ki的右孩子的编号是2i+1；否则，Ki无右孩子。

注：ki(0≤i≤n)满足数组下标时,则可能的左右孩子分别为2i+1、2i+2。

堆排序的思想（以大顶堆为例）

利用堆顶记录的是最大关键字这一特性，每一轮取堆顶元素放入有序区，就类似选择排序每一轮选择一个最大值放入有序区，可以把堆排序看成是选择排序的改进。

1. 将初始待排序关键字序列(R0,R1,R2....Rn)构建成大顶堆，此堆为初始的无序区；

2. 将堆顶元素R[0]与最后一个元素R[n]交换，此时得到新的无序区(R0,R1,R2,......Rn-1)和新的有序区(Rn)；

3. 由于交换后新的堆顶R[0]可能违反堆的性质，因此需要对当前无序区(R0,R1,R2,......Rn-1)调整为新堆。

不断重复此2、3步骤直到有序区的元素个数为n-1，则整个排序过程完成。

算法分析

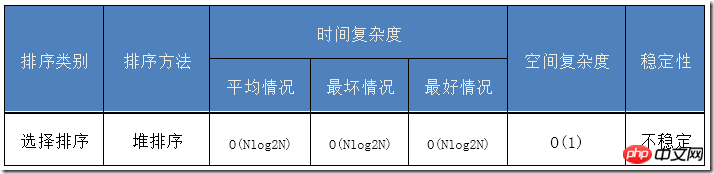
筛选算法

//最难理解的地方

• 目标：一个所有子树都为堆的完全二叉树。意思就是这个二叉树只差跟节点不满足堆的结构。//很重要，很重要，很重要

    如下图：

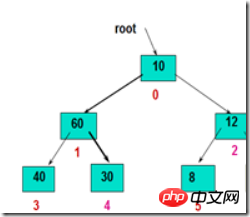
• 方法：首先将root和它的左右子树的根结点进行比较，把最大的元素交换到root节点；然后顺着被破坏的路径一路调整下去，直至叶子结点，就得到新的堆。

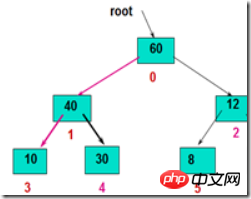
• 运用：1.在上文提到的堆排序思想，2-3步骤中将无序区调整为堆的时候用到。

          2.初始化堆

初始化堆

从最后一个非叶子节点i（i=n/2,n为节点个数）开始，将以i为根节点的二叉树通过筛选调整为堆。以第一张图为例，编号顺序为8、7、6...1。

从最后一个非叶子节就保证了筛选算法的正确性，因为筛选算法的目标是一个所有子树都为堆的完全二叉树。

php实现堆排序：
<?php
//堆排序，对简单排序的改进
  function swap(array &$arr,$a,$b)
  {
      $temp=$arr[$a];
      $arr[$a]=$arr[$b];
      $arr[$b]=$temp;
  }
  //调整$arr[$start]的关键字，$arr[$start]、$arr[$start+1]、、、$arr[$end]成为一个大根堆（根节点最大的完全二叉树）
  //注意：这里节点s的左右孩子是 2*s +1 和 2*s+2(数组开始下标为0时)
   function HeapAdjust(array &$arr $start $end)
   {
       $temp= $arr[$start];
       //沿关键字较大的孩子节点向下筛选
       //左右孩子计算 （这里数组的开始下标为0）
       //左边孩子 2*$start+1,右边孩子 2*$start+2
       for ($j=2*$start+1; $j <=$end; $j=2*$j+1) { 
           if ($j !=$end &&$arr[$j] <$arr[$j+1]) {
               $j++;  //转化为右边孩子
           }
           if ($temp >=$arr[$j]) {
               break;  //已经满足大根堆
           }
           //将根节点设置为子节点的较大值
           $arr[$start]=$arr[$j];
           //继续往下
           $start=$j;
       }
       $arr[$start] =$temp;
   }
   function HeapSort(array &$arr)
   {
       $count=count($arr);
       //先将数据结构造成大根堆 （由于是完全二叉树，所以这里用floor($count/2-1),下标小于或等于这个数的节点都是有孩子的节点)
       for ($i=floor($count /2)-1; $i >=0 ; $i--) { 
           HeapAdjust($arr,$i,$count);
       }
       for ($i=$count-1; $i >=0 ; $i--) { 
       //将堆顶元素与最后一个元素交换，获取到最大元素(交换后的最后一个元素)，将最大元素放到数组末尾
           swap($arr,0,$i);
       //经过交换，将最后一个元素（最大元素）脱离大根堆，并将未经排序的新数（$arr[0...$i-1]）重新调整为大根堆
           HeapAdjust($arr,0,$i-1);
       }
   }
   $arr=array(4,1,5,9);
   HeapSort($arr);
   v

相关推荐：

PHP堆排序实现代码

JavaScript中的堆排序详解

PHP排序算法之堆排序详解

以上是php堆排序详解的详细内容。更多信息请关注PHP中文网其他相关文章！