本篇文章给大家带来的内容是关于Java实现二分查找的基本方法（附代码），有一定的参考价值，有需要的朋友可以参考一下，希望对你有所帮助。
二分查找特别好理解，就类似于快排和归并当中用到的分治的思想，每次取中间数与目标数相比较，然后确定是大了还是小了，区间折半。
就比如：
小红选中了1-100中的某个数字（这个数字是56），要小明来猜，产生如下对话：
小明第一次猜测：68
小红：大了
小明第二次猜测：35
小红：小了
小明第三次猜测：58
小红：大了
小明第四次猜测：49
小红：小了
小明第五次猜测：54
小红：小了
小明第六次猜测：56
小红：bingo！！！
我们可以看到在上面的对话中，小明每次猜测都可以缩小区间，直到回答正确
二分查找就是这样的，比如我们现在有数组8，11，19，23，27，33，45，55，67，98，用二分查找如下图：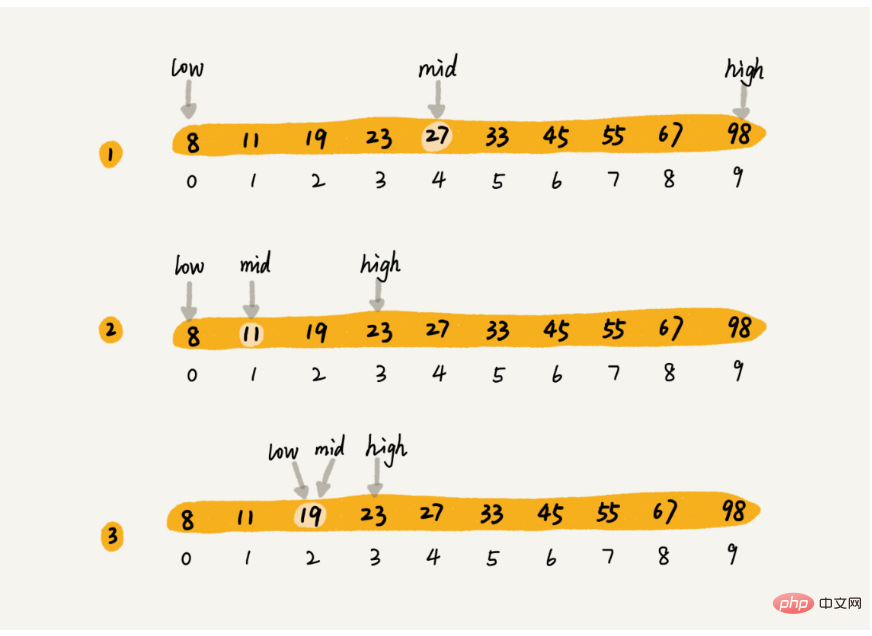
每次都可以缩小一半的区间，我们可以看到区间变化如下：
当区间大小无限接近1的时候k = log2n，所以时间复杂度为O(logn)。
是不是特别好理解，下面是我用Java实现的简单的二分查找（备注：是最简单的实现，二分查找的变体很复杂还没掌握）
package com.structure.search;
/**
* 二分查找法
*
* @author zhangxingrui
* @create 2019-02-15 21:29
**/
public class BinarySearch {
public static void main(String[] args) {
int[] nums = new int[]{4, 6, 9, 19, 30, 40, 500, 3450, 50004, 4334343};
System.out.println(binarySearch(nums, 0, nums.length - 1, 30));
System.out.println(binarySearch(nums, 50004));
}
/**
* @Author: xingrui
* @Description: 二分查找法（针对有序数组且不存在重复元素-递归方式实现）
* @Date: 21:37 2019/2/15
*/
private static int binarySearch(int[] nums, int p, int r, int k){
if(p > r)
return -1;
int mid = (p + r) / 2;
if(nums[mid] == k)
return mid;
if(k > nums[mid])
return binarySearch(nums, mid + 1, r, k);
else
return binarySearch(nums, p, mid - 1, k);
}
/**
* @Author: xingrui
* @Description: 二分查找法（针对有序数组且不存在重复元素-循环实现）
* @Date: 21:37 2019/2/15
*/
private static int binarySearch(int[] nums, int k){
int p = 0;
int r = nums.length - 1;
while (p <= r){
int mid = (p + r) / 2;
if(nums[mid] == k)
return mid;
if(k > nums[p])
p = mid + 1;
else
r = mid - 1;
}
return -1;
}
}代码很简单，其中需要注意的就是边界条件p<=r。
从代码也可以看出，简单实现有很大的局限性，只能适用于有序的不存在重复数据的数组。
并且二分查找不太适合小规模的数据查询（因为小规模的数据查询没有必要），这个好理解；同时呢，也不适合太大的数据的查询，这又是为啥子呢？
就是因为上面提到的：二分查找适合底层使用数组的数据，但是数组呢又是一段连续的内存空间，当数据很大的时候如果要用二分查找，那么数据的底层实现就
只能用数组，这样就不太好了。假设我的数据有一个G，那么我就要申请1个G的连续内存空间，妈哟，怕吃饱球了。
以上是Java实现二分查找的基本方法（附代码）的详细内容。更多信息请关注PHP中文网其他相关文章！
