二分搜索法,它充分利用了元素间的次序关系,采用分治策略,可在最坏的情况下用O(log n)完成搜索任务。
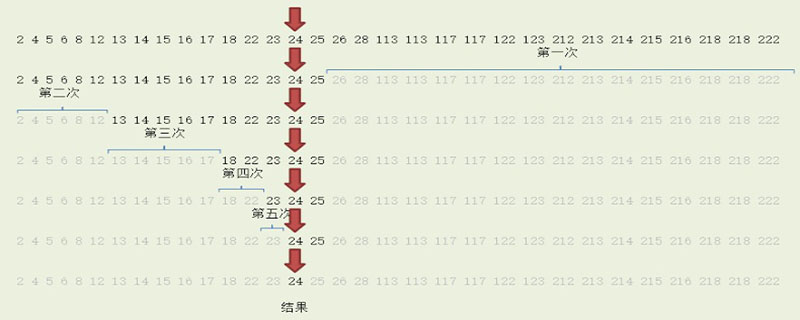
它的基本思想是,将n个元素分成个数大致相同的两半,取a[n/2]与欲查找的x作比较,如果x=a[n/2]则找到x,算法运算终止。 (推荐学习:web前端视频教程)
在计算机科学中,二分搜索(英语:binary search),也称折半搜索(英语:half-interval search)、对数搜索(英语:logarithmic search),是一种在有序数组中查找某一特定元素的搜索算法。
搜索过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜索过程结束;如果某一特定元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找,而且跟开始一样从中间元素开始比较。
如果在某一步骤数组为空,则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。
如果x
二分搜索法的应用极其广泛,而且它的思想易于理解,但是要写一个正确的二分搜索算法也不是一件简单的事。第一个二分搜索算法早在1946年就出现了,但是第一个完全正确的二分搜索算法直到1962年才出现。
Bentley在他的著作《Writing Correct Programs》中写道,90%的计算机专家不能在2小时内写出完全正确的二分搜索算法。
问题的关键在于准确地制定各次查找范围的边界以及终止条件的确定,正确地归纳奇偶数的各种情况,其实整理后可以发现它的具体算法是很直观的。
复杂度计算
时间复杂度:二分搜索每次把搜索区域砍掉一半,很明显时间复杂度为O(log n)。(n代表集合中元素的个数)
空间复杂度:O(1)。虽递归形式定义,但是尾递归,可改写为循环。
以上是二分搜索技术的时间复杂度的详细内容。更多信息请关注PHP中文网其他相关文章!


