由三个结点可以构造出多少种不同的二叉树

由三个结点可以构造出5种不同的二叉树。
相关知识点介绍:
什么是二叉树?
二叉树(Binary tree)是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式,即使是一般的树也能简单地转换为二叉树,而且二叉树的存储结构及其算法都较为简单,因此二叉树显得特别重要。
二叉树特点:
每个结点最多只能有两棵子树,且有左右之分。
二叉树是n个有限元素的集合,该集合或者为空、或者由一个称为根(root)的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成,是有序树。当集合为空时,称该二叉树为空二叉树。在二叉树中,一个元素也称作一个结点。
以上是由三个结点可以构造出多少种不同的二叉树的详细内容。更多信息请关注PHP中文网其他相关文章!

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

热门话题
 节点从Proxmox VE彻底撤离及再次加入集群
Feb 21, 2024 pm 12:40 PM
节点从Proxmox VE彻底撤离及再次加入集群
Feb 21, 2024 pm 12:40 PM
节点从ProxmoxVE彻底撤离及再次加入集群场景描述当ProxmoxVE集群中有节点损坏无法快速修复时,需要将故障节点干净的从集群踢出,并把残留信息清理干净。否则,新的节点用故障节点曾使用用的IP的地址将不能正常加入集群;同样,从集群中脱离出来的故障节点修复后,虽然与集群已经毫无关系,但访问此单节点的Web管理后台,将出现原ProxmoxVE集群其它节点的信息,非常恼火。从集群中驱逐节点如果ProxmoxVE是Ceph超融合集群,需要登录集群任意节点(欲删除节点除外)宿主系统Debian,命令
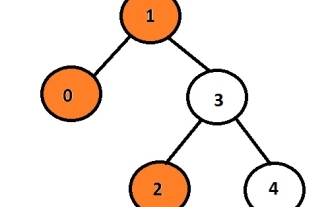 在C语言中打印二叉树的左视图
Sep 03, 2023 pm 01:25 PM
在C语言中打印二叉树的左视图
Sep 03, 2023 pm 01:25 PM
任务是打印给定二叉树的左节点。首先,用户将插入数据,从而生成二叉树,然后打印所形成的树的左视图。每个节点最多可以有2个子节点,因此这里程序必须仅遍历与节点关联的左指针如果左指针不为空,则意味着它将有一些与之关联的数据或指针,否则它将是要打印并显示为输出的左子级。示例Input:10324Output:102这里,橙色节点代表二叉树的左视图。在给定的图中,数据为1的节点是根节点,因此它将被打印,而不是转到左子节点,它将打印0,然后它将转到3并打印其左子节点,即2。我们可以使用递归方法来存储节点的级
 CentOS7系统安装和配置 DRBD?实现高可用性和数据冗余教程!
Feb 22, 2024 pm 02:13 PM
CentOS7系统安装和配置 DRBD?实现高可用性和数据冗余教程!
Feb 22, 2024 pm 02:13 PM
DRBD(DistributedReplicatedBlockDevice)是一种用于实现数据冗余和高可用性的开源解决方案。下面是在CentOS7系统上安装和配置DRBD的教程:安装DRBD:打开终端并以管理员身份登录到CentOS7系统。运行以下命令以安装DRBD软件包:sudoyuminstalldrbd配置DRBD:编辑DRBD配置文件(通常位于/etc/drbd.d目录下),配置DRBD资源的设置。例如,可以定义主节点和备份节点的IP地址、端口和设备等。确保主节点和备份节点之间可以通过网
 教你如何搭建K8S集群。
Feb 18, 2024 pm 05:00 PM
教你如何搭建K8S集群。
Feb 18, 2024 pm 05:00 PM
搭建Kubernetes(K8S)集群通常涉及多个步骤和组件配置。以下是一个简要的搭建Kubernetes集群的指南:准备环境:至少两台运行Linux操作系统的服务器节点,这些节点将用于搭建集群。这些节点可以是物理服务器或虚拟机。确保所有节点之间的网络连通性,并且它们可以相互访问。安装Docker:在每个节点上安装Docker,以便能够在节点上运行容器。可以根据不同的Linux发行版使用相应的包管理工具(如apt、yum)安装Docker。安装Kubernetes组件:在每个节点上安装Kuber
 Java中的二叉树结构详解
Jun 16, 2023 am 08:58 AM
Java中的二叉树结构详解
Jun 16, 2023 am 08:58 AM
二叉树是计算机科学中常见的数据结构,也是Java编程中常用的一种数据结构。本文将详细介绍Java中的二叉树结构。一、什么是二叉树?在计算机科学中,二叉树是一种树形结构,每个节点最多有两个子节点。其中,左侧子节点比父节点小,右侧子节点则比父节点大。在Java编程中,常用二叉树表示排序,搜索以及提高对数据的查询效率。二、Java中的二叉树实现在Java中,二叉树
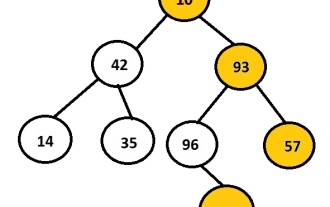 在C语言中,将二叉树的右视图打印出来
Sep 16, 2023 pm 11:13 PM
在C语言中,将二叉树的右视图打印出来
Sep 16, 2023 pm 11:13 PM
任务是打印给定二叉树的右节点。首先用户将插入数据以创建二叉树,然后打印所形成的树的右视图。上图展示了使用节点10、42、93、14、35、96、57和88创建的二叉树,其中选择并显示在树的右侧的节点。例如,10、93、57和88是二叉树的最右节点。示例Input:1042931435965788Output:10935788每个节点都有两个指针,即左指针和右指针。根据这个问题,程序只需遍历右节点。因此,不需要考虑节点的左子节点。右视图存储了所有那些是其所在层级的最后一个节点的节点。因此,我们可以
 如何使用Python实现二叉树的遍历
Jun 09, 2023 pm 09:12 PM
如何使用Python实现二叉树的遍历
Jun 09, 2023 pm 09:12 PM
作为一种常用的数据结构,二叉树经常被用来存储数据、搜索和排序。遍历二叉树是非常常见的操作之一。Python作为一种简单易用的编程语言,有许多方法可以实现二叉树的遍历。本文将介绍如何使用Python实现二叉树的前序、中序和后序遍历。二叉树的基础在学习二叉树的遍历之前,我们需要了解二叉树的基本概念。二叉树由节点组成,每个节点都有一个值和两个子节点(左子节点和右子
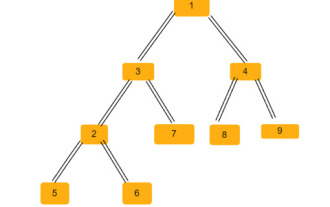 二叉树中等腰三角形的数量
Sep 05, 2023 am 09:41 AM
二叉树中等腰三角形的数量
Sep 05, 2023 am 09:41 AM
二叉树是一种数据结构,其中每个节点最多可以有两个子节点。这些孩子分别称为左孩子和右孩子。假设我们得到了一个父数组表示,您必须使用它来创建一棵二叉树。二叉树可能有几个等腰三角形。我们必须找到该二叉树中可能的等腰三角形的总数。在本文中,我们将探讨几种在C++中解决这个问题的技术。理解问题给你一个父数组。您必须以二叉树的形式表示它,以便数组索引形成树节点的值,而数组中的值给出该特定索引的父节点。请注意,-1始终是根父节点。下面给出的是一个数组及其二叉树表示。Parentarray=[0,-1,3,1,





