链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的；简单来说，线性表的链式存储结构生成的表，称作“链表”。链表中每个数据元素都由两部分组成：1、本身的信息，称为“数据域”；2、指向直接后继的指针，称为“指针域”。这两部分信息组成数据元素的存储结构，称之为“结点”；n个结点通过指针域相互链接，组成一个链表。
本教程操作环境：windows7系统、Dell G3电脑。
数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下，精心选择的数据结构可以带来更高的运行或者存储效率。数据结构往往同高效的检索算法和索引技术有关。
数据结构中的链表
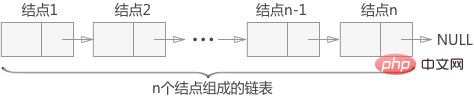
链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点（链表中每一个元素称为结点）组成，结点可以在运行时动态生成。
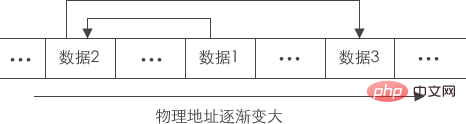
逻辑结构上一个挨一个的数据，在实际存储时，并没有像顺序表那样也相互紧挨着。恰恰相反，数据随机分布在内存中的各个位置，这种存储结构称为线性表的链式存储。
由于分散存储，为了能够体现出数据元素之间的逻辑关系，每个数据元素在存储的同时，要配备一个指针，用于指向它的直接后继元素，即每一个数据元素都指向下一个数据元素（最后一个指向NULL(空)）。
如上图所示，当每一个数据元素都和它下一个数据元素用指针链接在一起时，就形成了一个链，这个链子的头就位于第一个数据元素，这样的存储方式就是链式存储。
线性表的链式存储结构生成的表，称作“链表”。
链表中数据元素的构成
每个元素本身由两部分组成：
本身的信息，称为“数据域”；
指向直接后继的指针，称为“指针域”。
这两部分信息组成数据元素的存储结构，称之为“结点”。n个结点通过指针域相互链接，组成一个链表。
头结点、头指针和首元结点
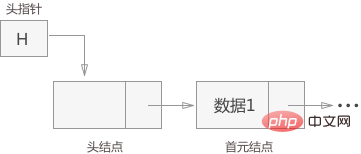
头结点：有时，在链表的第一个结点之前会额外增设一个结点，结点的数据域一般不存放数据（有些情况下也可以存放链表的长度等信息），此结点被称为头结点。
若头结点的指针域为空（NULL），表明链表是空表。头结点对于链表来说，不是必须的，在处理某些问题时，给链表添加头结点会使问题变得简单。
首元结点：链表中第一个元素所在的结点，它是头结点后边的第一个结点。
头指针：永远指向链表中第一个结点的位置（如果链表有头结点，头指针指向头结点；否则，头指针指向首元结点）。
头结点和头指针的区别：头指针是一个指针，头指针指向链表的头结点或者首元结点；头结点是一个实际存在的结点，它包含有数据域和指针域。两者在程序中的直接体现就是：头指针只声明而没有分配存储空间，头结点进行了声明并分配了一个结点的实际物理内存。
使用链表结构可以克服数组链表需要预先知道数据大小的缺点，链表结构可以充分利用计算机内存空间，实现灵活的内存动态管理。但是链表失去了数组随机读取的优点，同时链表由于增加了结点的指针域，空间开销比较大。链表最明显的好处就是，常规数组排列关联项目的方式可能不同于这些数据项目在记忆体或磁盘上顺序，数据的存取往往要在不同的排列顺序中转换。
特点
线性表的链式存储表示的特点是用一组任意的存储单元存储线性表的数据元素（这组存储单元可以是连续的，也可以是不连续的）。因此，为了表示每个数据元素 与其直接后继数据元素 之间的逻辑关系，对数据元素 来说，除了存储其本身的信息之外，还需存储一个指示其直接后继的信息（即直接后继的存储位置）。由这两部分信息组成一个"结点"（如下图所示），表示线性表中一个数据元素。线性表的链式存储表示，有一个缺点就是要找一个数，必须要从头开始找起，十分麻烦。
根据情况，也可以自己设计链表的其它扩展。但是一般不会在边上附加数据，因为链表的点和边基本上是一一对应的（除了第一个或者最后一个节点，但是也不会产生特殊情况）。不过有一个特例是如果链表支持在链表的一段中把前和后指针反向，反向标记加在边上可能会更方便。
对于非线性的链表，可以参见相关的其他数据结构，例如树、图。另外有一种基于多个线性链表的数据结构：跳表，插入、删除和查找等基本操作的速度可以达到O(nlogn），和平衡二叉树一样。
其中存储数据元素信息的域称作数据域（设域名为data），存储直接后继存储位置的域称为指针域（设域名为next）。指针域中存储的信息又称做指针或链。
由分别表示,，…，的N 个结点依次相链构成的链表，称为线性表的链式存储表示，由于此类链表的每个结点中只包含一个指针域，故又称单链表或线性链表。
链表插入和移除节点
链表允许插入和移除表上任意位置上的节点，但是不允许随机存取。
1、向链表中插入结点
链表中插入头结点，根据插入位置的不同，分为3种：
插入到链表的首部，也就是头结点和首元结点中间；
插入到链表中间的某个位置；
插入到链表最末端；
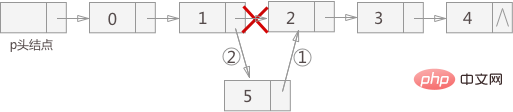
虽然插入位置有区别，都使用相同的插入手法。分为两步，如上图 所示：
将新结点的next指针指向插入位置后的结点；
将插入位置前的结点的next指针指向插入结点；
提示：在做插入操作时，首先要找到插入位置的上一个结点，图4中，也就是找到结点 1，相应的结点 2 可通过结点 1 的 next 指针表示，这样，先进行步骤 1，后进行步骤 2，实现过程中不需要添加其他辅助指针。
2、从链表中删除节点
当需要从链表中删除某个结点时，需要进行两步操作：
将结点从链表中摘下来;
手动释放掉结点，回收被结点占用的内存空间;
更多相关知识，请访问常见问题栏目！
以上是链表是什么数据结构的详细内容。更多信息请关注PHP中文网其他相关文章！
