如何证明一个问题是VNP问题?计算机科学家找到了一种简单方法
P/NP 问题是计算复杂度领域至今未解决的一个问题。人们一直试图找到一个问题的答案:「我们能否在合理时间内有效解决所有的计算问题?」
什么是合理的时间?实际上在宇宙终结之前能够解决的问题都算在合理时间内。然而许多问题似乎都难以在合理的时间内解决,这需要用数学来证明这些问题的难度。
2021 年的一项研究解答了上述问题,该研究证实:很大一部分问题都很难有效解决。
华盛顿大学的 Paul Beame 评价这项研究称:「就像攀登山峰一样,这项研究是计算理论研究路上的一个落脚点。」

该研究的三位研究者:计算机科学家 Srikanth Srinivasan(左)、Nutan Limaye(右上)和 Sébastien Tavenas。
该研究考虑的问题只涉及加法和乘法,但当这些问题仅限于以特定方式(加法和乘法的某种交替模式)解决时,它们就变得非常困难。
令人惊讶的是,该研究没有使用新的框架或工具,相反,作者设法绕过了由普林斯顿高等研究院数学学院教授 Wigderson 与耶路撒冷希伯来大学 Noam Nisan 合作数十年的工作中描述的数学障碍。
研究者之一、丹麦奥胡斯大学的 Srikanth Srinivasan 说:「我们意识到有一种非常简单的方法可以绕过这个障碍。并且,如果用这么简单的方法就能做到我们认为不可能的事情,那么肯定能找到更好的方法。」
重要的问题
计算机出现之后,科学家们发现计算机算法可以解决许多问题,但有时这些算法花费的时间太长——比实际计算时间更长。
他们开始怀疑有些问题是本质上难度太大,无论问题的规模是大是小都难以解决。例如在图中,一个重要的问题是确定是否存在一条哈密顿路径,即存在一条路径通过且仅通过每个顶点一次。增加点(和边)的数量应需要更长的时间来确定是否存在这样的路径,但即便是最好的算法,随着图规模的增加,花费的时间也会呈指数增长,这使得解决这个问题变得不切实际。
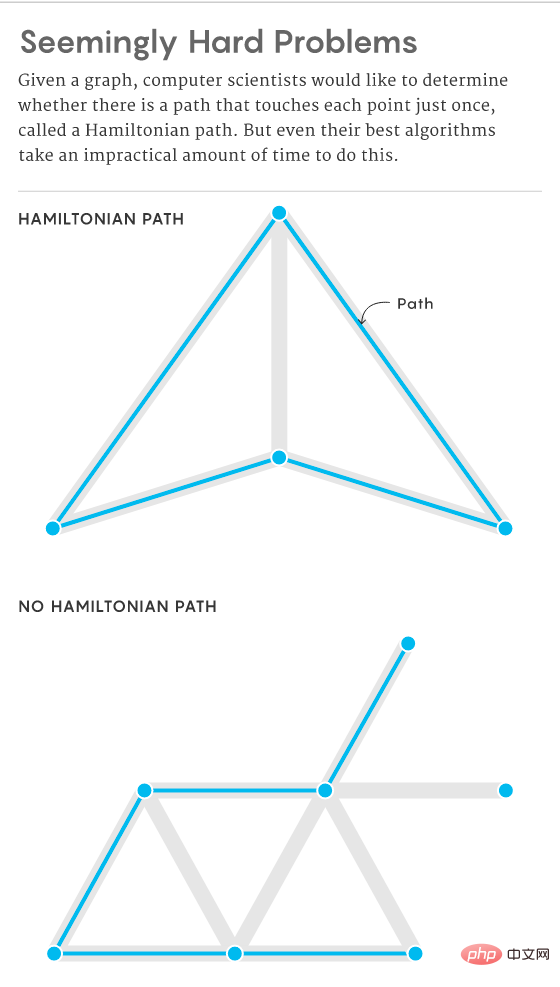
计算机科学家试图证明,任何能够以某种方式有效解决某类问题中一个难题的算法,都可以转化为对其他类似困难问题的解决方法,他们称这一类问题为 NP 问题。
当然,也有很多看起来不难的问题,不需要花费太多时间来解决。这些问题中的很多在某种意义上也是等价的,这类问题被称为 P 问题。他们认为 NP 问题确实比 P 问题更难,并且 NP 问题永远无法有效解决。但如果没有证据,这种想法就可能是错误的。
因此,计算机科学家们开始寻找方法来证明 NP 问题确实更难,这需要证明 NP 问题必须要指数级的时间才能解决,但证明这一点并不容易。
多难才算「困难(hard)」?
设想一组只需要加法和乘法的特定问题。例如,给定一组点,可以仅通过加法和乘法,用关于点的数据来计算所有可能的哈密顿路径(如果存在的话)。
随着问题规模的增加,一些算术问题(如计算哈密顿路径)需要更多的时间。1979 年,哈佛大学的 Leslie Valiant 证明许多算术问题在「难度」上是等价的,而其他的则在「没有难度」上是等价的。计算机科学家后来以他的名字命名这两类问题——分别是 VNP 和 VP。
和 P 与 NP 问题一样,我们无法证明 VNP 问题的难度,我们只知道 VNP 问题比 NP 问题更难,因为它建立在后者的基础之上,例如计算路径首先需要确定路径是否存在。
「这比 NP 难,因此证明这很困难应该更容易」,Shpilka 说道。
在随后的几十年中,计算机科学家在 VP 与 VNP 问题上取得的进展比他们在 P 与 NP 问题上取得的进展要大得多,但其中大部分仅限于 Valiant 创建的称为代数复杂性的子领域。在 Limaye、Srinivasan 和 Tavenas 最近的工作之前,他们仍然很难判断是否存在一般意义上的算术问题。
调整多项式
这项新工作有助于探究计算机科学家思考加法和乘法问题的方式。从数学上讲,这些问题完全可以写作多项式的形式(例如 x^2 + 5y + 6),这些多项式由相加和相乘的变量组成。
对于任何特定问题,例如计算哈密顿路径,你可以构建一个表示它的多项式。例如你可以用一个变量来表示每个点和边,这样当添加更多点和边时,就可以向多项式添加更多变量。
为了证明计算哈密顿路径这样的算术问题很困难,就需要证明当添加更多点和边时,相应的多项式需要以指数时间解决更多操作。例如,x^2 需要一次操作(x * x),而 x^2 + y 需要两次操作(x * x 然后加上 y)。操作的数量称为多项式的大小。
但是多项式的大小很难确定。例如多项式 x^2 + 2x + 1。它的大小似乎为 4(两次乘法和两次加法),但是该多项式可以重写为两个和的乘积,(x + 1)(x + 1),它的操作数更少——两次加法,一次乘法。通常,随着问题的规模扩大和将更多变量添加到多项式中,数学变换可以帮助简化和缩小其规模。
在 Valiant 的研究几年之后,计算机科学家找到了一种方法,可以使问题的大小更易于分析。为此,他们提出了一个称为「深度(depth)」的属性,它指定多项式在和与乘积之间切换或交替的次数。例如,多项式 x^2 + 2x + 1 的深度为 2,因为它是乘积之和(如 x^2 和 2x)。相比之下,表达式 (x + 1)(x + 1) 的深度为 3,因为它的深度与 0 + (x + 1)(x + 1) 相同,按照乘积之和计算。
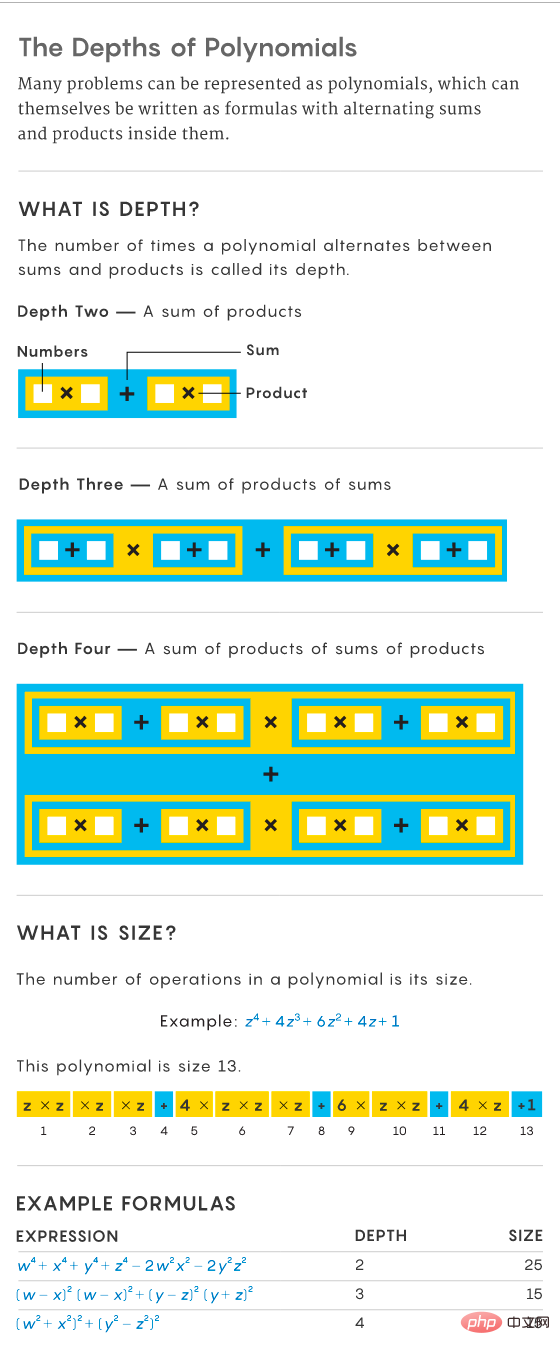
为了简化多项式,计算机科学家将它们限制为一种固定形式,并具有称为「恒定深度」的属性,其中和、乘积的模式不会随着问题的增长而改变。这使得它们的大小更加固定,多项式的大小会随着其深度的增加而减小。某个恒定深度的表达式称为公式。恒定深度让多项式的研究取得了更多进展。
神奇的「深度」
1996 年, Nisan 和 Wigderson 的一篇论文专注于解决矩阵乘法的问题,他们用两种方式简化了这个问题。首先,他们用恒定深度的公式来表示它——深度为 3。其次,他们只考虑了具有某种简单结构的公式,其中每个变量的最大指数为 1,这使得原问题成为「多线性」问题。
计算机科学家已经发现,某些问题可以转换为相对简单的集合多线性(set-multilinear)结构,代价是多项式的大小呈次指数增长(与指数增长的增长率相当)。
Nisan 和 Wigderson 随后表明了随着矩阵的扩大,矩阵乘法问题需要指数级的时间来解决。换句话说,他们证明了一个重要的问题是困难的,为证明一类问题都是困难的做出了努力。然而,他们的结果只适用于具有简单的、集合多线性结构的公式。

Leslie Valiant
增加多项式的深度往往会导致其大小减小。随着时间的推移,计算机科学家使这两个属性之间的权衡变得更精确。他们表明,将两个深度级别添加到深度 3、集合多线性多项式可以平衡其集合多线性结构的大小增益。如果深度 5 的结构化公式需要指数时间,那么具有一般、非结构化性质的深度 3 公式也是如此。
Srikanth Srinivasan 等人的新工作表明,矩阵乘法问题的深度 5 集合多线性公式确实以与指数级速度增长。这意味着一般的深度 3 公式也需要指数时间。随后他们证明类似的规律适用于所有深度(不止是 3 和 5)。有了这种关系,他们就证明了对于同一个问题,任何深度的一般公式的大小都会随着问题的规模而以指数速度增长。
他们还表明用一个恒定深度的公式表示矩阵乘法是很难的,无论该深度是多少。
该研究的结果首次提供了对于算术问题何时是「困难」的一般理解——当它不能用恒定深度的公式表示时即为困难。矩阵乘法的具体问题已知是 VP 问题。并且已知 VP 问题在不限于恒定深度时相对容易,因此结果得出恒定深度为问题「困难」的来源。
VNP 问题是否比 VP 问题更难?新结果并没有直接说明这一点,他们只表明恒定深度公式很难。但这仍然是证明 VNP 问题不能等价于 VP 问题的重要里程碑。
对于更大的 P 与 NP 问题,我们现在可以对有一天能找到答案更加乐观了。毕竟为了解决困难的问题,我们首先需要知道哪些方向是无望的。
以上是如何证明一个问题是VNP问题?计算机科学家找到了一种简单方法的详细内容。更多信息请关注PHP中文网其他相关文章!

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

Video Face Swap
使用我们完全免费的人工智能换脸工具轻松在任何视频中换脸!

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

热门话题
 CUDA之通用矩阵乘法:从入门到熟练!
Mar 25, 2024 pm 12:30 PM
CUDA之通用矩阵乘法:从入门到熟练!
Mar 25, 2024 pm 12:30 PM
通用矩阵乘法(GeneralMatrixMultiplication,GEMM)是许多应用程序和算法中至关重要的一部分,也是评估计算机硬件性能的重要指标之一。通过深入研究和优化GEMM的实现,可以帮助我们更好地理解高性能计算以及软硬件系统之间的关系。在计算机科学中,对GEMM进行有效的优化可以提高计算速度并节省资源,这对于提高计算机系统的整体性能至关重要。深入了解GEMM的工作原理和优化方法,有助于我们更好地利用现代计算硬件的潜力,并为各种复杂计算任务提供更高效的解决方案。通过对GEMM性能的优
 word文档怎么计算加减乘除
Mar 19, 2024 pm 08:13 PM
word文档怎么计算加减乘除
Mar 19, 2024 pm 08:13 PM
WORD是一个强大的文字处理器,我们可以利用word进行各种文字的编辑,在Excel表格当中,我们已经熟练掌握了加减乘数的运算方法,那么如果需要在Word表格里,计算数值的加减乘数,该如何操作呢,难道只能用计算器计算吗?答案当然是否定的,WORD也同样可以完成。今天小编就来教大家如何在Word文档的表格当中,运用公式计算加减乘除等基本运算,一起来学习一下吧。那么,今天就让小编具体演示一下,WORD文档怎么计算加减乘除?第一步:打开一个WORD,单击工具栏【插入】下的【表格】,在下拉菜单当中插入一
 深入探讨模型、数据和框架:一份详尽的54页高效大语言模型综述
Jan 14, 2024 pm 07:48 PM
深入探讨模型、数据和框架:一份详尽的54页高效大语言模型综述
Jan 14, 2024 pm 07:48 PM
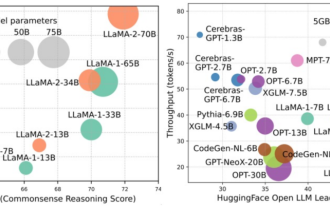
大规模语言模型(LLMs)在许多重要任务中展现出了引人注目的能力,包括自然语言理解、语言生成和复杂推理,并对社会产生了深远的影响。然而,这些出色的能力却需要大量的训练资源(如左图所示)和较长的推理时间(如右图所示)。因此,研究人员需要开发有效的技术手段来解决它们的效率问题。此外,从图的右侧还可以看出,一些高效的LLMs(LanguageModels)如Mistral-7B,已经成功应用于LLMs的设计和部署中。这些高效的LLMs在保持与LLaMA1-33B相近的准确性的同时,能够大大减少推理内存
 如何使用Python的count()函数计算列表中某个元素的数量
Nov 18, 2023 pm 02:53 PM
如何使用Python的count()函数计算列表中某个元素的数量
Nov 18, 2023 pm 02:53 PM
如何使用Python的count()函数计算列表中某个元素的数量,需要具体代码示例Python作为一种强大且易学的编程语言,提供了许多内置函数来处理不同的数据结构。其中之一就是count()函数,它可以用来计算列表中某个元素的数量。在本文中,我们将详细介绍如何使用count()函数,并提供具体的代码示例。count()函数是Python的内置函数,用于计算某
 使用行列式计算三角形面积的Java程序
Aug 31, 2023 am 10:17 AM
使用行列式计算三角形面积的Java程序
Aug 31, 2023 am 10:17 AM
简介使用行列式计算三角形面积的Java程序是一个简洁高效的程序,可以根据给定三个顶点的坐标来计算三角形的面积。该程序对于学习或使用几何的任何人都非常有用,因为它演示了如何在Java中使用基本算术和代数计算,以及如何使用Scanner类读取用户输入。程序提示用户输入三角形三个点的坐标,然后将其读入并用于计算坐标矩阵的行列式。使用行列式的绝对值来确保面积始终为正,然后使用公式计算三角形的面积并显示给用户。该程序可以轻松修改以接受不同格式的输入或执行附加计算,使其成为几何计算的多功能工具。决定因素行列
 碾压H100,英伟达下一代GPU曝光!首个3nm多芯片模块设计,2024年亮相
Sep 30, 2023 pm 12:49 PM
碾压H100,英伟达下一代GPU曝光!首个3nm多芯片模块设计,2024年亮相
Sep 30, 2023 pm 12:49 PM
3纳米制程,性能超越H100!最近,据外媒DigiTimes爆料,英伟达正在开发下一代GPU,代号为「Blackwell」的B100据称,作为面向人工智能(AI)和高性能计算(HPC)应用的产品,B100将采用台积电的3nm工艺制程,以及更为复杂的多芯片模块(MCM)设计,并将于2024年第四季度现身。对于垄断了人工智能GPU市场80%以上份额的英伟达来说,则可以借着B100趁热打铁,在这波AI部署的热潮中进一步狙击AMD、英特尔等挑战者。根据英伟达的估计,到2027年,该领域的产值预计将达到约
 在Java中递归地计算子字符串出现的次数
Sep 17, 2023 pm 07:49 PM
在Java中递归地计算子字符串出现的次数
Sep 17, 2023 pm 07:49 PM
给定两个字符串str_1和str_2。目标是使用递归过程计算字符串str1中子字符串str2的出现次数。递归函数是在其定义中调用自身的函数。如果str1是"Iknowthatyouknowthatiknow",str2是"know"出现次数为-3让我们通过示例来理解。例如输入str1="TPisTPareTPamTP",str2="TP";输出Countofoccurrencesofasubstringrecursi
 如何使用C#中的Math.Pow函数计算指定数的幂次方
Nov 18, 2023 am 11:32 AM
如何使用C#中的Math.Pow函数计算指定数的幂次方
Nov 18, 2023 am 11:32 AM
在C#中,有一个Math类库,其中包含许多数学函数。其中包括计算幂次方的函数Math.Pow,它可以帮助我们计算指定数的幂。Math.Pow函数的用法非常简单,只需要指定底数和指数就可以了。其语法如下:Math.Pow(base,exponent);其中base表示底数,exponent表示指数。该函数返回double类型的结果,即幂次方的计算结果。下面让






