因果推断主要技术思想与方法总结

导读:因果推断是数据科学的一个重要分支,在互联网和工业界的产品迭代、算法和激励策略的评估中都扮演者重要的角色,结合数据、实验或者统计计量模型来计算新的改变带来的收益,是决策制定的基础。然而,因果推断并不是一件简单的事情。首先,在日常生活中,人们常常把相关和因果混为一谈。相关往往代表着两个变量具有同时增长或者降低的趋势,但是因果意味着我们想要知道对一个变量施加改变的时候会发生什么样的结果,或者说我们期望得到反事实的结果,如果过去做了不一样的动作,未来是否会发生改变?然而难点在于,反事实的数据往往是真实世界中难以观察和收集的。
本文回顾因果推断的两个流派——潜在结果模型Rubin Causal Model (RCM; Rubin 1978) 和结构因果模型Causal Diagram (Pearl 1995)的主要技术思想和方法,以及近年来的新方法和应用。笔者由于学术背景和计量经济学较为相关,所以引用的方法和论文主要参考了经济学的文献,可能在一些方法的理论和应用上的深度与广度上有所疏漏,请读者谅解。
潜在结果模型
我们把每个研究对象或者用户用i来表示,他们可能会受到一定的策略干预:Ti=1代表受到了干预(实验组),Ti=0代表没有受到干预(基准组),对应的我们关心的结果分别是Yi0和Yi1,但是只有一种情况会真实发生,也就是说Yi0和Yi1只能观察到其中一个,另一个未知。这里我们期望得到的因果推断结果是平均处理效应ATE=E[Y1-Y0]。
我们可以通过一定的数学推导来解释估计ATE的困难之处。由于我们只会观察到Yi0和Yi1中的一个,我们能够直接计算的其实是实验组和基准组之间的组间差异E[Yi1|Ti=1]-E[Yi0|Ti=0],这个差值进一步可以拆解等于E[Yi1|Ti=1]-E[Yi0|Ti=1]+E[Yi0|Ti=1]-E[Yi0|Ti=0]。其中E[Yi1|Ti=1]-E[Yi0|Ti=1]是实验组个体上的平均处理效应(ATT),ATT和ATE往往并不相等,这两者的差异代表着我们计算的外在效度(External Validity)。如果样本局限在某个年龄段的用户,那么结果不一定能够推广到全年龄段的用户上,说明我们的分析不一定具备外在效度。上面公式里的第二部分E[Yi0|Ti=1]-E[Yi0|Ti=0]代表了样本的选择性偏差。选择性偏差在实际生活中常常可能不是0,例如如果实验组和基准组不是随机抽样而来,会在一定的特征分布上有差异,那么就可能会造成选择性偏差。因此,我们计算的组间差异其实是只有当消除选择性偏差、具备外在效度,并且基于大量充足的样本的时候,才代表着我们期望得到的平均处理效应。潜在效果模型的思想方法其实就是通过一定的设定和模型达到这样的条件。其思想背后,还有比较严格的数学假设。下面我们按照不同方法,分别回顾其主要思想和近年来的技术发展与应用,受篇幅限制,断点回归方法这里就没有展开做详细介绍了。
1、A/B测试
潜在效果模型最常见的方法就是随机实验,或者说是我们在工业界中常用到的A/B测试。我们通过一定的随机性抽样构造实验组和基准组,来观察组间的差异。但是需要指出的是,即便满足了随机性,这里因果推断的有效性还需要满足一个重要的假设——Stable Unit Treatment Value Assumption (SUTVA)。每个个体的潜在结果只和他自己有关,与其他个体是否被实验策略干预无关,同时我们所关心的单个策略干预没有不同形式或强度来导致不同的潜在结果。在现实生活中SUTVA假设违背的场景中有很多,也激发了各种新型A/B测试技术手段的发展,例如针对挤占问题的预算或者策略控制,亦或者是分流设计的改进。我们这里举一些分流相关的例子:
在LinkedIn,实验人员采用网络抽样的实验方法来应对社交网络对于传统个体随机试验的挑战。首先将用户分成不同的cluster,每个cluster作为一个个体来随机分流和测算实验指标,通过估计用户的网络效应exposure来修正估计的处理效应(Gui et al. 2015)。
在Airbnb等平台,买家和卖家之间常常存在着相互影响,也会干扰传统的实验方法。研究者通过双边实验设计和库存的动态模型来构造实验评估指标(Johari et al. 2022)。需要指出的是,双边实验是个比较崭新的领域,其实验设计可以帮助实验者发现传统单边实验的溢出效应,但是对于实验结果如何做统计推断和修正是比较困难并且不一定有绝对答案的,要更多地结合业务场景来探讨。
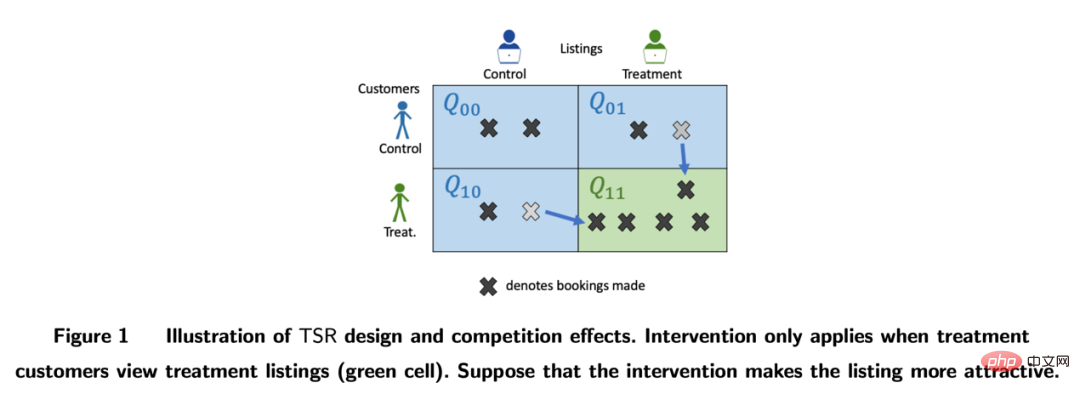
图片来自论文Johari et al. (2022)
2、工具变量法
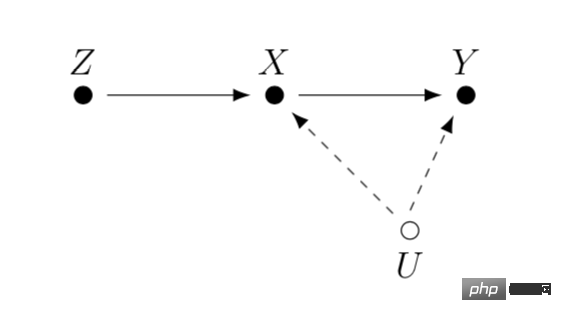
工具变量是解决线性回归问题内生性的一种方法。接下来我们介绍一下内生性问题和如何通过工具变量解决内生性。内生性的主要问题是如果我们关心X对Y的影响,但是存在无法测量到的变量U,且U会同时影响X和Y。那么X具有内生性,U即上文提到的混淆变量。如果我们能找到一个跟X有关的变量Z,且Z与U不相关。那我们可以通过Z作为工具变量来估计X对Y的因果效应,具体计算方法一般是两阶段最小二乘法。工具变量法在实际使用的时候,要注意避免“弱工具变量”的问题,也就是工具变量Z和关心的变量X相关度很低,这样会造成估计的因果效应有偏差,可以依赖统计检验方法来确认这样的问题是否存在。
工具变量法的一个发展是和深度学习模型相结合,例如Hartford et al. (2017) 提出的Deep IV方法。这一研究将传统工具变量的两阶段最小二乘法转化成更灵活的两个深度神经网络的预测任务,放松了传统方法中对于数据生成过程(DGP)的强假设。
在实际的应用中,基于互联网大量A/B测试积累的场景,我们可以通过实验的meta-learning和工具变量法来学习指标间的因果关系。例如Peysakhovich & Eckles (2018) 利用Facebook的数据,将实验组信息作为工具变量,在两阶段最小二乘法的基础上结合L0正则化,可以解决传统工具变量法在有限样本上的bias问题,也能克服现实情况中大量实验观察到的效果绝对值比较低(“弱工具变量”)的问题。
工具变量的思想除了学习指标间的影响关系外也可以用于解决推荐系统中的偏差问题。在推荐系统中,模型的训练往往依赖用户的历史观看和转评赞的反馈行为,但是这些历史数据往往被展示的位置、曝光的模式等混淆因素所影响,快手和人大的研究者Si et al. (2022)利用工具变量的思想提出IV4Rec框架,将搜索的query作为工具变量来分解推荐系统embedding中的因果和非因果关系,和深度学习相结合,在快手数据和公开数据集MIND上都能验证提升推荐模型的效果。
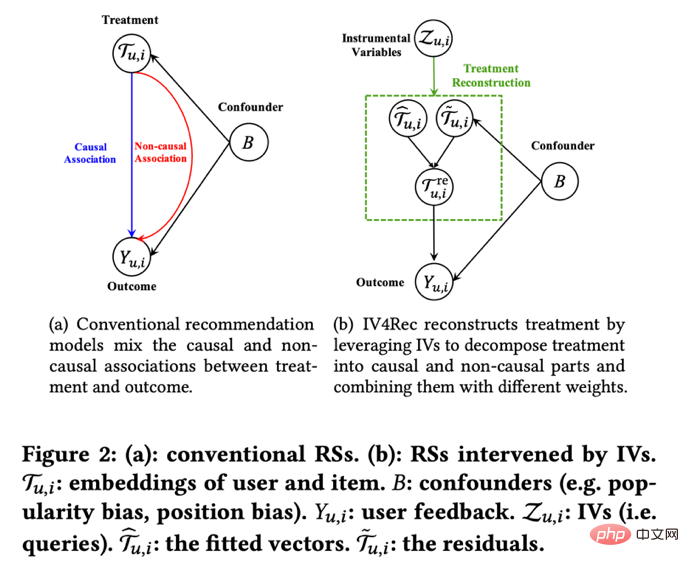
图片来自论文Si et al. (2022)
3、匹配法
匹配(Matching)是被业务广泛使用的一种因果分析方法,主要是为了解决当实验组和控制组由于某种原因(confounder)不可比的时候,通过给实验组的每一个用户匹配和他在某些特征上最相似(CEM粗粒度匹配)或者接受干预概率(propensity score)最相似(PSM倾向性得分匹配)的控制组用户,重新制造可比的实验组和控制组。匹配是最近似AB/RCT(randomized controlled trial)随机实验的方法,操作方法比较类似,结果很直观。并且,匹配是一种非参数估计处理效应的方法,不受制于一般的线性参数模型假设。通过匹配之后的样本,也可以搭配双重差分的方法,常用于解决新功能渗透率较低的问题。近年来,匹配法的发展主要是结合机器学习模型将倾向性得分匹配做得更加精准,同时这里的思想也应用到了一些其他因果方法、机器学习模型的纠偏中,相关内容后文讲到的时候会涉及。
4、面板数据的系列方法和发展
近年来,围绕着面板数据的因果推断有着比较多的新方法来出现。我们先回顾传统的面板数据方法。
最常用的是双重差分的方法。最简单的双重差分是控制组间差异,用回归模型的形式来描述yit=α0+α1Treati+α2Postt+α3Treati*Postt。这里Treati=1代表个体是否受到干预,Postt=1代表干预后观测的时间周期。通过下表,我们可以发现α2+α3是实验组在实验日期前后的差分值,α2是对照组在实验日期前后的差分值。对这两项做差,α3即为因果效应的估计,也是上述模型中交互项的系数,并且就是两次差分的结果。
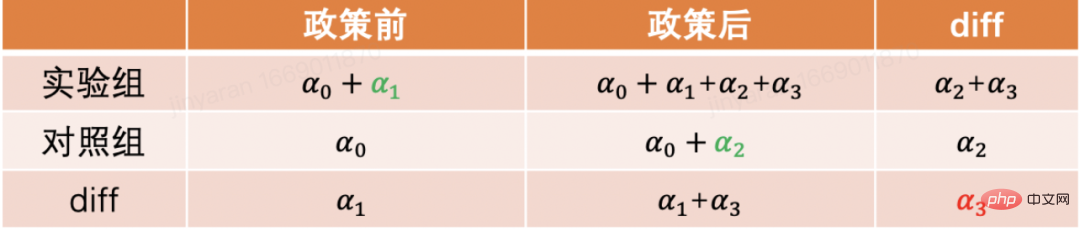
双重差分法依赖比较严格的假设。“平行趋势”是最重要的前提,也就是实验组和基准组再政策干预发生前结果指标的均值随着时间趋势稳定,这预示着除了政策干预本身其他因素影响对于实验组和基准组是相同的。我们可以使用时间趋势图来检验平行假设,一些统计推断包也会提供相应的功能。当平行检验不通过的时候,可以通过在回归中加入控制变量或者时间趋势项来进一步检验。在一些情况下,也可以借助三重差分法来解决。此外在实际实践中,双重差分法有比较多的实现方式。除了上文所述方式之外,也可以采取“双向固定效应模型”的设定Yit=τTreatit+Xitβ+αi+ξt+εit,但也会依赖强假设:不存在随时间变化的混淆因素,并且过去的结果不会影响当期的处理状态,同时也要求政策的处理效应保持不变。关于背后的理论和方法的局限性,以及拓展出的匹配和再加权等新方法,推荐结合斯坦福大学徐轶青教授的课程来进行学习:
https://yiqingxu.org/teaching/
下面我们列举一些比较常用的新方法:
合成控制法是面板数据因果推断方法中衍生出的一套方法,也在不断的有新的估计或者统计推断检验研究出现。当干预实施在一个群体或者一个地区的时候,实验组在一个时间点上只有一个观测值,并且数据的时间周期较长,例如某个城市做地推活动,通常不适用于双重差分的方法,这时候可以采取合成控制法。其原理就是挑选一些对照城市,拟合成一个在干预前和实验组极其相似的“虚拟对照组”,详细的理论介绍和近年来的优化可以参考麻省理工大学Aberto Abadie教授及其合作者的论文(Abadie, Diamond and Hainmueller 2010)和他在NBER的短期课程来进行进一步学习:
https://www.nber.org/lecture/2021-summer-institute-methods-lecture-alberto-abadie-synthetic-controls-methods-and-practice
双重差分法和合成控制法其实都可以统一在一套分析框架体系内。研究Arkhangelsky et al. (2021)指出,双重差分是在解决一个没有任何个体或者时间上加权的双向固定效应回归问题,而合成控制法是在政策干预发生前的个体施加权重ω来拟合被干预的个体,这篇论文结合两种方法提出了一个新的估计量:合成双重差分(SDID),既包括个体上的权重ω,也包括时间上的权重λ,从而提升了整体估计量的稳健性效果。这里的时间的权重λ可以理解为和干预发生后更相似的时期的数据时期被赋予了更高的权重。
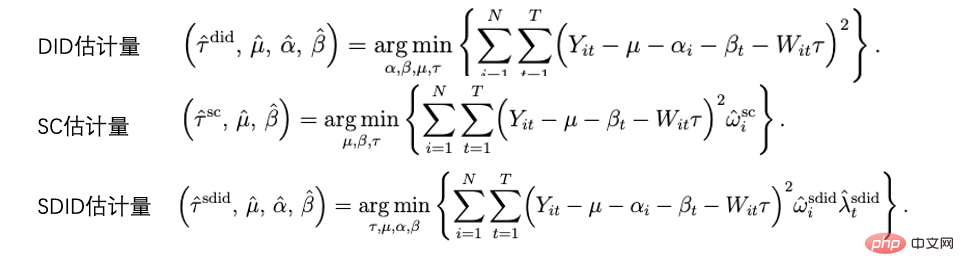
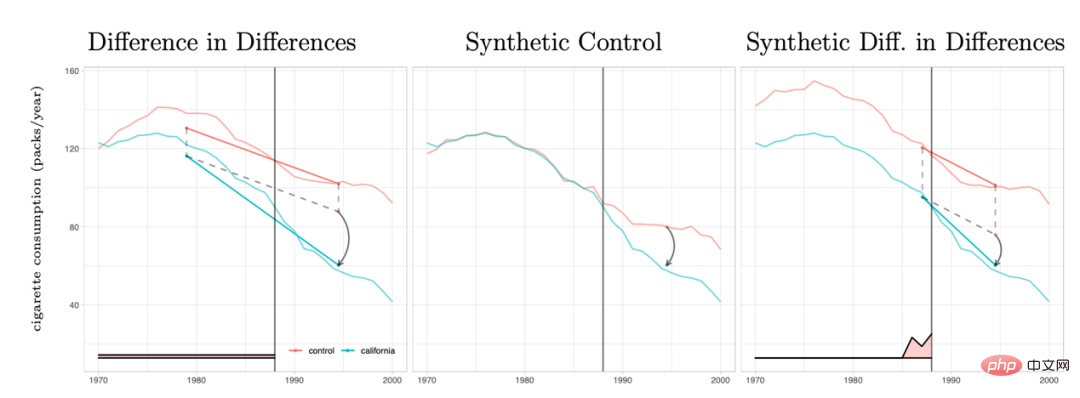
几种方法的比较:图片来自论文Arkhangelsky et al. (2021)
面板数据也可以结合矩阵补全的方法做因果推断,这也是近年来这个领域的一个新发展。矩阵补全的算法是通过解一个凸优化问题来解决因果推断面临的反事实数据的缺失问题。这种方法适用于个体被政策干预时间不一致的情况,例如一个产品的迭代需要用户更新产品版本才生效,但是用户更新的时间不一致。详细的方法理论可以参考Athey et al. (2021)等相关论文。矩阵补全、合成控制还有随机干预下的回归预测方法也都可以统一在优化问题的框架下,进而我们也可以通过ensemble方式结合多种方法得到更稳健的估计结果(Athey et.al 2019)。

矩阵补全示意图:图片来自Guidon Imbens在AEA的课程,此处用W代表treatment状态 https://www.aeaweb.org/conference/cont-ed/2018-webcasts
以上在这一部分我们介绍了面板数据因果推断的主要方法和进展 ,这个领域是一个方法非常多样化、进展非常快的领域,但是对于应用者而言要求需要充分思考方法背后的假设和局限性,才能更加准确的评估实际中的各种政策,受篇幅限制这里我们只是做了非常简要的介绍。
5、异质性因果效应的方法综述
结合机器学习方法来研究异质性因果效应其实是最近几年来因果推断发展的潮流。我们首先介绍一下异质性因果效应:异质性因果效应(Heterogeneous Treatment Effect,简称HTE)是指由于样本个体特征不同,实验在个体上产生不同效果的现象。结合数学公式来表述,HTE有很多种形式:
每个个体的因果效应ITE (individual treatment effect):τi=Yi1-Yi0,Yi1和Yi0只有一个能观测到,另一个和τi需要通过一定的模型方法进行估计。
在某些特征上的群体的平均因果效应,这里我们用X代表特征,那么估计的是CATE (conditional average treatment effect)是限定特征上去某些特定值的群体上的平均因果效应: τ(x)=E[Y1-Y0|X=x]。
HTE的分析方法目前有广泛的应用场景。通过HTE,我们可以知道对某种策略干预反应最大的群体有哪些特征,也可以帮助我们排查一个A/B测试有预期效果或者没效果的策略的作用机制如何,还可以应用于各种个性化策略当中。异质性因果推断的方法在工业界和互联网有非常多的应用,比如在TripAdvisor用来测算在会员注册激励,在微软用这类方法和短期数据测算不同项目的长期ROI,详细的应用案例可以参考2021的KDD培训课程(https://causal-machine-learning.github.io/kdd2021-tutorial/)。
最常见的异质性因果效应的方法其实是实验分析中常用的多维分析,但多维分析的使用需要警惕多重检验的问题。同时,当维度足够多时,对于实验样本量也有比较高的要求,同时分析效率比较低。而机器学习方法,则提供了一些提升效率的挖掘手段,它的好处是可以自适应地学习异质性因果效应的分布,不需要严格的函数形式假设,比传统基于线性回归的计量经济学方法或者多维分析的方法有更强的自由度,但对于技术上的挑战是如何做统计推断。近年来随着机器学习和计量经济学的结合不断深入,也有多套方法在这一领域有所创新和应用,这里我们重点介绍以下几类方法,这些方法成立的基本假设都是条件独立假设(Conditional Independence Assumption),也就是说只有当各种混淆变量控制的足够充分时,我们才能得到相对准确的因果效应估计。
因果森林:基于随机森林,是直接进行拟合估计法的非参方法。因果树的主要估计逻辑是通过定义每片叶子上的因果效应,来定义整体树的loss function。因果树旨在根据某种切分X的方式,最大化所有叶片的loss的和。和机器学习中的树算法除了估计的目标不同之外,还有一个差异点是在因果推断的算法中一般会将训练集样本分成训练集和估计集,训练集用于分叶,估计集用于分叶后计算每个叶子节点上的平均处理效应。因果树的优点是结果非常简洁易懂,可以通过分桶的方式直接明确实验效果在哪些人群上有明确的差异,最先分桶的指标往往是最因果效果差异性的最大的维度。但是因果树容易过拟合,在实际工作中推荐使用因果随机森林(细节可参考Athey and Imbens 2016, Wager and Athey 2018),同时因果随机森林也有比较好的统计推断性质。关于这一方法的拓展可以参考Athey, Tibshirani and Wager (2019)和Friedberg et al. (2020)等研究工作,这些新的方法可以进一步处理有混淆变量时的问题,以及更平滑地估计结果。
Meta Learners:和使用因果树直接估计因果效应的模型不同,它属于间接估计模型的一种:是通过对结果变量Y进行直接建模。因此Meta Learner不能将估计的HTE直接用于做统计推断,在实际应用过程中,一些研究者会采用bootstrap方式来解决这一问题。Meta Learners估计算法有3种:T-Learner, S-Learner, X-Learner。三种方法基本的区别在于:
最简单的是 S-learner。它将干预变量作为了一个特征变量进行一次建模,适合用在treatment和结果变量强相关的情况上,否则模型无法识别干预变量改变引起的结果的改变;
稍微复杂一点的是T-learner。其通过强制用两个模型分别学习实验组的Yi1和控制组Yi0而识别因果效应,适合用在实验组和控制组变量观测值较多且较平均的时候,否则其中一个模型会更被更重的regularized;
X-learner是一种较为新的方法,通过使用两步估计和用倾向性得分纠偏,可以在数据量较少的情况下做出较好的估计(更多细节参考Künzel et al. 2019)。
基于DML和DRL的估计框架:这两种框架我们结合微软公司的Econml工具来介绍:
https://www.microsoft.com/en-us/research/project/econml/
DML(double machine learning)双重机器学习是针对高维混淆变量存在的情况下,灵活混淆变量和处理变量、结果变量之间关系的一种框架性的方法,其方法顾名思义,在估计因果效应的时候主要分为两步:第一步用两种(不需要同样的)机器学习模型分别估计E(Y|X,W)和E(T|X,W)两个条件期望,然后取残差。这里X和W都是混淆变量,但只有X是CATE中相关的变量。第二步基于残差进行ATE或者CATE的估计,在估计CATE时,T-E(T|X,W)的残差前乘以一个关于X的函数θ(X)来进行估计。关于如何估计ATE可以参考Chernozhukov et al. (2018)。Econml在第二步提供了很多种模型来供选择:LinearDML(用OLS模型)、DML(用自定义的模型)、CausalForestDML(用因果随机森林)……。DML框架在使用的时候需要注意检验两个模型的残差项是否均值显著区别于0或者显著相关,如果是的话,说明混淆变量可能控制的不够多。
DRL框架则是基于Doubly Robust方法,也是分成两步,第一步使用X,W,T预测Y,定义预测值为gt(X,W);第二步用一个分类模型,用X,W预测T得到倾向性得分,定义为pt(X,W)。需要注意的是这里的T是离散变量,并且限制gt(X,W)某种regression-based model。两步结果之后则是计算一个调整后的结果变量:
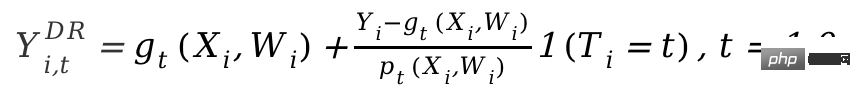
再将调整过后的Yi,tDR在实验组和控制组求差Yi1DR-Yi0DR,回归X得到CATE。DRL之所以叫Doubly Robust的原因在于,上述公式中gt(X,W)和pt(X,W)中只要有一个估计正确,因果效应估计就是无偏的。但如果两个模型估计都是错误的,那产生的误差可能会非常大。同DML类似,Econml中DRL的各种Learner的差异在于使用什么样的模型来用X拟合Yi1DR-Yi0DR。
基于机器学习模型的异质性因果推断方法最大的应用挑战其实是如何选择合适的机器学习模型并且调参,得到相对稳健的估计结果。根据应用经验和近年来的研究来说,有如下注意事项:
- 保证训练样本量足够大。
-
如果使用Econml工具,推荐用score*函数选择模型(score越小模型越佳),但不是每个模型都有该函数:如DML有但是X-Learner或者Causal Forest无。如果使用Uber的Causalml,则可以使用Cumulative Gain图来进行比较各种Meta Learner的表现。
https://github.com/uber/causalml。 - 一些方法是可以对HTE做统计检验的,但是另一些不能。在Econml中,可以对HTE做统计检验的方法仅限于DML/DRL中最后一步模型设定为线形模型的方法或者因果森林,而特征变量X和实验变量T在很多业务场景下都是非线性相关。强行选择线性模型可能会造成HTE估计偏误(如HTE的波动性和X无关,仅为噪音)。如果要筛选HTE显著的个体进行后续分析,需要进行个体效应检验的多重检验矫正。
- 除了模型拟合度还需要一个标准衡量HTE的估计好坏:如HTE的变化幅度是否大到能够区分敏感人群和非敏感人群,可参考Chernozhukov et al. (2018)提出的基于HTE特征的统计推断,也非常容易应用。
上述介绍的方法基本还是集中于一个干预变量下的静态的异质性因果效应。但是在实际应用中,我们会遇到的问题会更加复杂。例如涉及到多个干预变量:产品给用户的补贴激励中可能既包括签到激励,又包括一些其他任务的奖励,怎么平衡不同类型激励的分配可以定义成一个多干预变量的异质性因果效应建模和优化问题。再例如动态因果效应,混淆变量随着不同时间的干预会进行变化(可参考Lewis and Syrgkanis 2020)。还是以激励任务为例,这些任务可能使得用户关注了新的主播、从而改变了她们的观看内容的偏好,也会影响后续激励的效果。这些复杂场景都激发了各类方法的进一步拓展,我们也期待未来会有更成型、更有体系化的研究和应用涌现出来。
结构因果模型
在前一个部分我们介绍了潜在结果模型的主要思想和方法发展。这一类流派方法统计理论比较完善,可以得到比较准确的估计结果。但是也存在一定的局限性,只能用于估计变量之间一度相关的影响(i.e,只允许有一个因变量和一些自变量,不能估计间接影响的链路),去如何学习众多变量之间的链路和复杂关系,则需要用到另一个流派的结构因果模型方法。
结构因果模型用有向无环图 (directed acyclic graph;DAG) 来描述变量之间的因果关系和条件分布。图的每个节点是一个变量,因果关系由链接这些节点的边来表示,例如X12代表了X2影响了X1,我们也称X1为子节点,X2为父节点。对于一组随机变量X=(X1,X2,...,XP)形成的DAG,变量的联合分布可以表示成P(X)=∏pj=1P(Xj|paj),其中paj是Xj的紧邻的父节点。当我们表达因果关系的时候,则引入do 算子的概念,假设当前X=(X1,X2,...Xp)=(x1,x2,...xp),用do(Xj=x’j) 表示对于变量Xj干预(将其赋值为x’j),那么我们可以根据变量间的条件分布关系得到一个新的DAG:P(X1=x1,X2=x2,...,Xp=xp|do(Xj=x’j)),新老分布下每个其他变量的期望变化就是Xj对他们的因果作用,例如E(X1|do)(Xj=x’j)-E(X1|do(Xj=xj))。结果因果模型的开创者Judea Pearl在他的研究中指出,利用因果图来识别因果关系的时候,如果满足 “后门准则”和 “前门准则”,其实并不需要观测到所有的变量,关于具体的理论细节请参考Pearl (2009)。需要补充说明的是,结构因果模型和潜在结果模型其实也是存在关联的。

在实际应用中,我们不一定能够直接具备定义因果图的信息,因此如何学习变量间的因果图结构反而成为了重要的问题。在解决这类问题时,首先我们要明确所需的假设:
Causal Markov因果马尔可夫假设:该假设意味任何节点的条件分布仅基于其直接父节点。
Causal Sufficiency 因果充分性假设:该假设等同于不存在无法观测的混淆变量。
Causal Faithfulness 因果忠诚性假设:该假设意味基于一些条件概率分布,一些节点之间是独立的(因此图可以被切割)。
其算法大致分成两类:
详细介绍可以参考Glymour, Zhang and Sprites (2019)和《中国科学:数学》2018年12期的文章《因果推断的统计方法》:
https://cosx.org/2022/10/causality-statistical-method/。
Constraint-based Algorithms:基于条件分布独立检验学习出所有满足faithfulness和causal markov假设的因果图,即检验两个节点之间的条件分布是否独立。例如PC算法(Spirtes and Glymour 1991)和IC算法(Verma and Pearl 1990)。
Score-based Algorithms:通过最优化定义的某种score来寻找和数据最匹配的图结构。需要定义structural equations和score functions。例如CGNN算法(Goudet et al. 2017)和NOTEARS算法(Zheng et al. 2018)。这里我们着重介绍一下NOTEARS算法。传统的算法是基于在所有节点和节点间可能产生的关系的基础上,在所有可能生成的图中进行搜索,按照某个标准选出最优解决,这是典型的NP-hard的问题,耗时极长且目前的计算资源基本无法满足运算需求。NOTEARS算法将离散搜索的问题转化成了连续搜索的问题。该算法极大提高了运算速度,使得普通的数据分析师也可以使用。但这个方法也存在着一定的局限性,例如假设所有变量的噪声必须是高斯分布,近年来也有越来越多的方法(如He et al.2021)尝试改进这类方法的假设。
随着强化学习领域的发展,我们也发现因果推断和强化学习可以相互结合在一起,推动相互的发展。因果推断可以在强化学习中通过推断状态之间或状态与动作之间的因果关系,帮助强化学习算法更高效的学习价值函数或者最优策略,在这方面有兴趣的读者可以参考哥伦比亚大学教授Elias Bareinboim的课程(https://www.php.cn/link/ad16fe8f92f051afbf656271afd7872d)。在另一方面,强化学习也可以融入因果图的学习算法中,例如华为诺亚方舟实验室的研究Zhu, Ng, and Chen (2019)。
关于因果推断未来的展望,要提到近年来和图学习、因果推断、机器学习相关的一个新的研究范式,是清华大学崔鹏老师团队提出的“稳定学习”的概念(Cui and Athey 2022)。机器学习、人工智能等模型的应用依赖一个重要的假设——Independent and Identically Distributed(独立同分布)的假设。也就是说训练集、测试集需要来自同一个分布,但实际上存在各种各样的OOD(Out Of Distribution,分布外)问题,此时模型的性能无法保证,这也是历史以来各类模型面临的一个重要的技术风险。因果推断可以帮助克服这类问题。如果可以保证一个结构在各种各样的环境下都具有同等的预测效应从而克服OOD问题,那么这个结构一定是一个因果结构,而且一个因果结构在各种环境下的性能都是相对稳定的。崔鹏老师团队的研究(He et al. 2022, Shen et al. 2021)发现,利用混淆变量匹配平衡的思想,通过对样本进行重加权就可以使得所有的变量变得独立,使得一个基于关联的模型变成基于因果的模型。所谓的稳定学习,就是使用一种分布的训练集和多种不同的未知分布的测试集,优化的目标是最小化准确率的方差。相信在未来这是一个非常重要的领域,感兴趣的读者可以继续关注相关的研究进展。
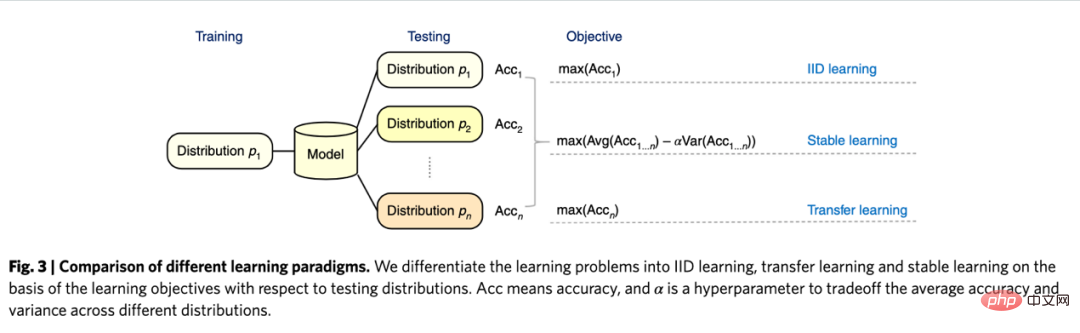
独立同分布学习、迁移学习、稳定学习的比较:图片来自论文 Cui and Athey 2022
在实际应用中,推荐系统、计算机视觉、自动驾驶、自然语言处理等机器学习、人工智能相关的领域都不乏因果推断和因果图学习的身影,推动了这些领域的发展,在这里我们也是列举一些近年来的例子,关于更详细地与机器学习相关的应用和benchmark模拟器、数据集可以参考UCL和牛津大学的研究者的总结(Kaddour et al. 2022)。在推荐系统领域,如我们在工具变量方法应用中的介绍,推荐系统不可避免地存在偏差,识别用户和物品之间的因果图关系可以帮助推荐系统纠偏。例如Wang et al. (2021)和Zhang et al. (2021)分别利用因果图来消除标题党和流行度带来的偏差。在自动驾驶领域,来自微软的研究者推出了一个模拟驾驶环境平台CausalCity(McDuff et al. 2022),将因果推断融入车辆的轨迹预测。在自然语言处理领域,研究者发现因果推断可以帮助NLP方法更加稳健和可理解(Zeng et al. 2020),包括检验语言模型和语料库中的偏见(Vig et al. 2020)……相信在未来,因果推断会继续蓬勃发展,在上述和其他领域发挥重要的作用。
以上是因果推断主要技术思想与方法总结的详细内容。更多信息请关注PHP中文网其他相关文章!

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

热门话题
 CLIP-BEVFormer:显式监督BEVFormer结构,提升长尾检测性能
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer:显式监督BEVFormer结构,提升长尾检测性能
Mar 26, 2024 pm 12:41 PM
写在前面&笔者的个人理解目前,在整个自动驾驶系统当中,感知模块扮演了其中至关重要的角色,行驶在道路上的自动驾驶车辆只有通过感知模块获得到准确的感知结果后,才能让自动驾驶系统中的下游规控模块做出及时、正确的判断和行为决策。目前,具备自动驾驶功能的汽车中通常会配备包括环视相机传感器、激光雷达传感器以及毫米波雷达传感器在内的多种数据信息传感器来收集不同模态的信息,用于实现准确的感知任务。基于纯视觉的BEV感知算法因其较低的硬件成本和易于部署的特点,以及其输出结果能便捷地应用于各种下游任务,因此受到工业
 使用C++实现机器学习算法:常见挑战及解决方案
Jun 03, 2024 pm 01:25 PM
使用C++实现机器学习算法:常见挑战及解决方案
Jun 03, 2024 pm 01:25 PM
C++中机器学习算法面临的常见挑战包括内存管理、多线程、性能优化和可维护性。解决方案包括使用智能指针、现代线程库、SIMD指令和第三方库,并遵循代码风格指南和使用自动化工具。实践案例展示了如何利用Eigen库实现线性回归算法,有效地管理内存和使用高性能矩阵操作。
 探究C++sort函数的底层原理与算法选择
Apr 02, 2024 pm 05:36 PM
探究C++sort函数的底层原理与算法选择
Apr 02, 2024 pm 05:36 PM
C++sort函数底层采用归并排序,其复杂度为O(nlogn),并提供不同的排序算法选择,包括快速排序、堆排序和稳定排序。
 人工智能可以预测犯罪吗?探索CrimeGPT的能力
Mar 22, 2024 pm 10:10 PM
人工智能可以预测犯罪吗?探索CrimeGPT的能力
Mar 22, 2024 pm 10:10 PM
人工智能(AI)与执法领域的融合为犯罪预防和侦查开辟了新的可能性。人工智能的预测能力被广泛应用于CrimeGPT(犯罪预测技术)等系统,用于预测犯罪活动。本文探讨了人工智能在犯罪预测领域的潜力、目前的应用情况、所面临的挑战以及相关技术可能带来的道德影响。人工智能和犯罪预测:基础知识CrimeGPT利用机器学习算法来分析大量数据集,识别可以预测犯罪可能发生的地点和时间的模式。这些数据集包括历史犯罪统计数据、人口统计信息、经济指标、天气模式等。通过识别人类分析师可能忽视的趋势,人工智能可以为执法机构
 改进的检测算法:用于高分辨率光学遥感图像目标检测
Jun 06, 2024 pm 12:33 PM
改进的检测算法:用于高分辨率光学遥感图像目标检测
Jun 06, 2024 pm 12:33 PM
01前景概要目前,难以在检测效率和检测结果之间取得适当的平衡。我们就研究出了一种用于高分辨率光学遥感图像中目标检测的增强YOLOv5算法,利用多层特征金字塔、多检测头策略和混合注意力模块来提高光学遥感图像的目标检测网络的效果。根据SIMD数据集,新算法的mAP比YOLOv5好2.2%,比YOLOX好8.48%,在检测结果和速度之间实现了更好的平衡。02背景&动机随着远感技术的快速发展,高分辨率光学远感图像已被用于描述地球表面的许多物体,包括飞机、汽车、建筑物等。目标检测在远感图像的解释中
 九章云极DataCanvas多模态大模型平台的实践和思考
Oct 20, 2023 am 08:45 AM
九章云极DataCanvas多模态大模型平台的实践和思考
Oct 20, 2023 am 08:45 AM
一、多模态大模型的历史发展上图这张照片是1956年在美国达特茅斯学院召开的第一届人工智能workshop,这次会议也被认为拉开了人工智能的序幕,与会者主要是符号逻辑学届的前驱(除了前排中间的神经生物学家PeterMilner)。然而这套符号逻辑学理论在随后的很长一段时间内都无法实现,甚至到80年代90年代还迎来了第一次AI寒冬期。直到最近大语言模型的落地,我们才发现真正承载这个逻辑思维的是神经网络,神经生物学家PeterMilner的工作激发了后来人工神经网络的发展,也正因为此他被邀请参加了这个
 算法在 58 画像平台建设中的应用
May 09, 2024 am 09:01 AM
算法在 58 画像平台建设中的应用
May 09, 2024 am 09:01 AM
一、58画像平台建设背景首先和大家分享下58画像平台的建设背景。1.传统的画像平台传统的思路已经不够,建设用户画像平台依赖数据仓库建模能力,整合多业务线数据,构建准确的用户画像;还需要数据挖掘,理解用户行为、兴趣和需求,提供算法侧的能力;最后,还需要具备数据平台能力,高效存储、查询和共享用户画像数据,提供画像服务。业务自建画像平台和中台类型画像平台主要区别在于,业务自建画像平台服务单条业务线,按需定制;中台平台服务多条业务线,建模复杂,提供更为通用的能力。2.58中台画像建设的背景58的用户画像
 实时加SOTA一飞冲天!FastOcc:推理更快、部署友好Occ算法来啦!
Mar 14, 2024 pm 11:50 PM
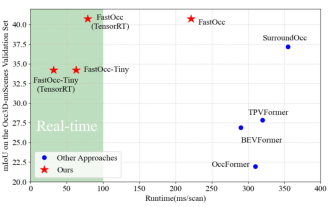
实时加SOTA一飞冲天!FastOcc:推理更快、部署友好Occ算法来啦!
Mar 14, 2024 pm 11:50 PM
写在前面&笔者的个人理解在自动驾驶系统当中,感知任务是整个自驾系统中至关重要的组成部分。感知任务的主要目标是使自动驾驶车辆能够理解和感知周围的环境元素,如行驶在路上的车辆、路旁的行人、行驶过程中遇到的障碍物、路上的交通标志等,从而帮助下游模块做出正确合理的决策和行为。在一辆具备自动驾驶功能的车辆中,通常会配备不同类型的信息采集传感器,如环视相机传感器、激光雷达传感器以及毫米波雷达传感器等等,从而确保自动驾驶车辆能够准确感知和理解周围环境要素,使自动驾驶车辆在自主行驶的过程中能够做出正确的决断。目






