
哈喽,大家好。
这是一个房价预测的案例,来源于 Kaggle 网站,是很多算法初学者的第一道竞赛题目。
该案例有着解机器学习问题的完整流程,包含EDA、特征工程、模型训练、模型融合等。
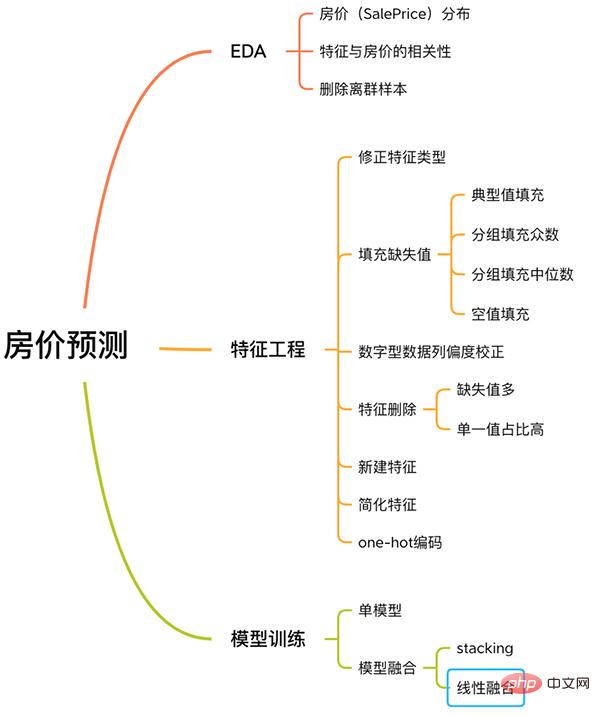
房价预测流程
下面跟着我,来学习一下该案例。
没有啰嗦的文字,没有多余的代码,只有通俗的讲解。
探索性数据分析(Exploratory Data Analysis,简称EDA) 的目的是让我们对数据集有充分的了解。在这一步,我们探索的内容如下:

EDA内容
train = pd.read_csv('./data/train.csv')
test = pd.read_csv('./data/test.csv')

训练样本
train和test分别是训练集和测试集,分别有 1460 个样本,80 个特征。
SalePrice列代表房价,是我们要预测的。
因为我们任务是预测房价,所以在数据集中核心要关注的就是房价(SalePrice) 一列的取值分布。
sns.distplot(train['SalePrice']);
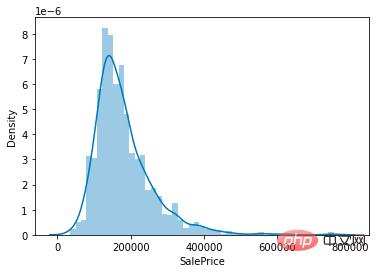
房价取值分布
从图上可以看出,SalePrice列峰值比较陡,并且峰值向左偏。
也可以直接调用skew()和kurt()函数计算SalePrice具体的偏度和峰度值。
对于偏度和峰度都比较大的情况,建议对SalePrice列取log()进行平滑。
了解完SalePrice的分布后,我们可以计算 80 个特征与SalePrice的相关关系。
重点关注与SalePrice相关性最强的 10 个特征。
# 计算列之间相关性
corrmat = train.corr()
# 取 top10
k = 10
cols = corrmat.nlargest(k, 'SalePrice')['SalePrice'].index
# 绘图
cm = np.corrcoef(train[cols].values.T)
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, square=True, fmt='.2f', annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()
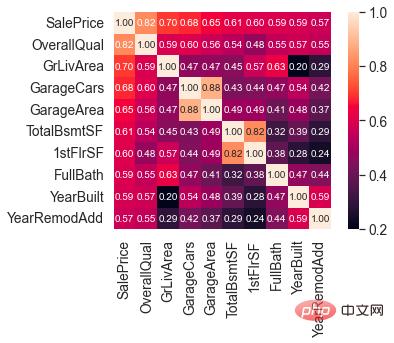
与SalePrice高度相关的特征
OverallQual(房子材料和装饰)、GrLivArea(地上居住面积)、GarageCars(车库容量)和 TotalBsmtSF(地下室面积)跟SalePrice有很强的相关性。
这些特征在后面做特征工程时也会重点关注。
由于数据集样本量很少,离群点不利于我们后面训练模型。
所以需要计算每个数值特性的离群点,剔除掉离群次数最多的样本。
# 获取数值型特征 numeric_features = train.dtypes[train.dtypes != 'object'].index # 计算每个特征的离群样本 for feature in numeric_features: outs = detect_outliers(train[feature], train['SalePrice'],top=5, plot=False) all_outliers.extend(outs) # 输出离群次数最多的样本 print(Counter(all_outliers).most_common()) # 剔除离群样本 train = train.drop(train.index[outliers])
detect_outliers()是自定义函数,用sklearn库的LocalOutlierFactor算法计算离群点。
到这里, EDA 就完成了。最后,将训练集和测试集合并,进行下面的特征工程。
y = train.SalePrice.reset_index(drop=True) train_features = train.drop(['SalePrice'], axis=1) test_features = test features = pd.concat([train_features, test_features]).reset_index(drop=True)
features合并了训练集和测试集的特征,是我们下面要处理的数据。
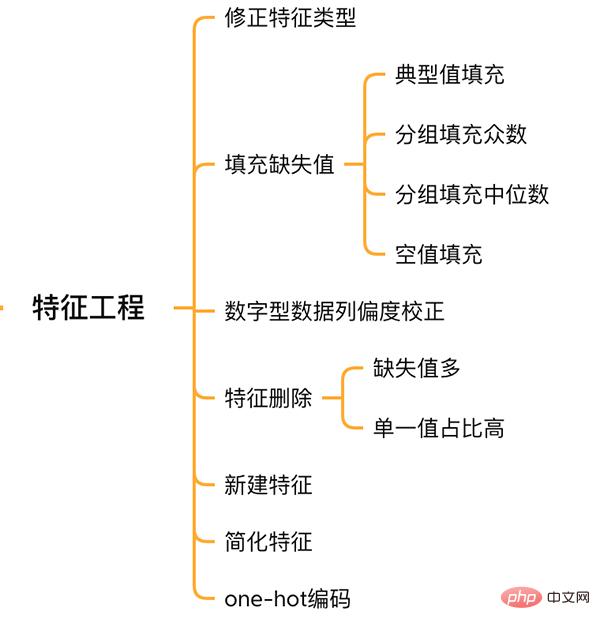
特征工程
MSSubClass(房屋类型)、YrSold(销售年份)和MoSold(销售月份)是类别型特征,只不过用数字来表示,需要将它们转成文本特征。
features['MSSubClass'] = features['MSSubClass'].apply(str) features['YrSold'] = features['YrSold'].astype(str) features['MoSold'] = features['MoSold'].astype(str)
填充缺失值没有统一的标准,需要根据不同的特征来决定按照什么样的方式来填充。
# Functional:文档提供了典型值 Typ
features['Functional'] = features['Functional'].fillna('Typ') #Typ 是典型值
# 分组填充需要按照相似的特征分组,取众数或中位数
# MSZoning(房屋区域)按照 MSSubClass(房屋)类型分组填充众数
features['MSZoning'] = features.groupby('MSSubClass')['MSZoning'].transform(lambda x: x.fillna(x.mode()[0]))
#LotFrontage(到接到举例)按Neighborhood分组填充中位数
features['LotFrontage'] = features.groupby('Neighborhood')['LotFrontage'].transform(lambda x: x.fillna(x.median()))
# 车库相关的数值型特征,空代表无,使用0填充空值。
for col in ('GarageYrBlt', 'GarageArea', 'GarageCars'):
features[col] = features[col].fillna(0)
跟探索SalePrice列类似,对偏度高的特征进行平滑。
# skew()方法,计算特征的偏度(skewness)。 skew_features = features[numeric_features].apply(lambda x: skew(x)).sort_values(ascending=False) # 取偏度大于 0.15 的特征 high_skew = skew_features[skew_features > 0.15] skew_index = high_skew.index # 处理高偏度特征,将其转化为正态分布,也可以使用简单的log变换 for i in skew_index: features[i] = boxcox1p(features[i], boxcox_normmax(features[i] + 1))
对于几乎都是缺失值,或单一取值占比高(99.94%)的特征可以直接删除。
features = features.drop(['Utilities', 'Street', 'PoolQC',], axis=1)
同时,可以融合多个特征,生成新特征。
有时候模型很难学习到特征之间的关系,手动融合特征可以降低模型学习难度,提升效果。
# 将原施工日期和改造日期融合 features['YrBltAndRemod']=features['YearBuilt']+features['YearRemodAdd'] # 将地下室面积、1楼、2楼面积融合 features['TotalSF']=features['TotalBsmtSF'] + features['1stFlrSF'] + features['2ndFlrSF']
可以发现,我们融合的特征都是与SalePrice强相关的特征。
最后简化特征,对分布单调的特征(如:100个数据中有99个的数值是0.9,另1个是0.1),进行01处理。
features['haspool'] = features['PoolArea'].apply(lambda x: 1 if x > 0 else 0) features['has2ndfloor'] = features['2ndFlrSF'].apply(lambda x: 1 if x > 0 else 0)
到这里特征工程就做完了, 我们需要从features中将训练集和测试集重新分离出来,构造最终的训练数据。
X = features.iloc[:len(y), :] X_sub = features.iloc[len(y):, :] X = np.array(X.copy()) y = np.array(y) X_sub = np.array(X_sub.copy())
因为SalePrice是数值型且是连续的,所以需要训练一个回归模型。
首先以岭回归(Ridge) 为例,构造一个k折交叉验证模型。
from sklearn.linear_model import RidgeCV from sklearn.pipeline import make_pipeline from sklearn.model_selection import KFold kfolds = KFold(n_splits=10, shuffle=True, random_state=42) alphas_alt = [14.5, 14.6, 14.7, 14.8, 14.9, 15, 15.1, 15.2, 15.3, 15.4, 15.5] ridge = make_pipeline(RobustScaler(), RidgeCV(alphas=alphas_alt, cv=kfolds))
岭回归模型有一个超参数alpha,而RidgeCV的参数名是alphas,代表输入一个超参数alpha数组。在拟合模型时,会从alpha数组中选择表现较好某个取值。
由于现在只有一个模型,无法确定岭回归是不是最佳模型。所以我们可以找一些出场率高的模型多试试。
# lasso lasso = make_pipeline( RobustScaler(), LassoCV(max_iter=1e7, alphas=alphas2, random_state=42, cv=kfolds)) #elastic net elasticnet = make_pipeline( RobustScaler(), ElasticNetCV(max_iter=1e7, alphas=e_alphas, cv=kfolds, l1_ratio=e_l1ratio)) #svm svr = make_pipeline(RobustScaler(), SVR( C=20, epsilon=0.008, gamma=0.0003, )) #GradientBoosting(展开到一阶导数) gbr = GradientBoostingRegressor(...) #lightgbm lightgbm = LGBMRegressor(...) #xgboost(展开到二阶导数) xgboost = XGBRegressor(...)
有了多个模型,我们可以再定义一个得分函数,对模型评分。
#模型评分函数 def cv_rmse(model, X=X): rmse = np.sqrt(-cross_val_score(model, X, y, scoring="neg_mean_squared_error", cv=kfolds)) return (rmse)
以岭回归为例,计算模型得分。
score = cv_rmse(ridge)
print("Ridge score: {:.4f} ({:.4f})n".format(score.mean(), score.std()), datetime.now(), ) #0.1024
运行其他模型发现得分都差不多。
这时候我们可以任选一个模型,拟合,预测,提交训练结果。还是以岭回归为例
# 训练模型
ridge.fit(X, y)
# 模型预测
submission.iloc[:,1] = np.floor(np.expm1(ridge.predict(X_sub)))
# 输出测试结果
submission = pd.read_csv("./data/sample_submission.csv")
submission.to_csv("submission_single.csv", index=False)
submission_single.csv是岭回归预测的房价,我们可以把这个结果上传到 Kaggle 网站查看结果的得分和排名。
有时候为了发挥多个模型的作用,我们会将多个模型融合,这种方式又被称为集成学习。
stacking 是一种常见的集成学习方法。简单来说,它会定义个元模型,其他模型的输出作为元模型的输入特征,元模型的输出将作为最终的预测结果。
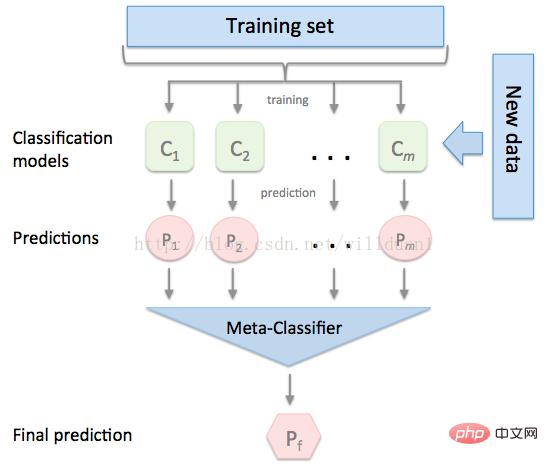
stacking
这里,我们用mlextend库中的StackingCVRegressor模块,对模型做stacking。
stack_gen = StackingCVRegressor( regressors=(ridge, lasso, elasticnet, gbr, xgboost, lightgbm), meta_regressor=xgboost, use_features_in_secondary=True)
训练、预测的过程与上面一样,这里不再赘述。
多模型线性融合的思想很简单,给每个模型分配一个权重(权重加和=1),最终的预测结果取各模型的加权平均值。
# 训练单个模型 ridge_model_full_data = ridge.fit(X, y) lasso_model_full_data = lasso.fit(X, y) elastic_model_full_data = elasticnet.fit(X, y) gbr_model_full_data = gbr.fit(X, y) xgb_model_full_data = xgboost.fit(X, y) lgb_model_full_data = lightgbm.fit(X, y) svr_model_full_data = svr.fit(X, y) models = [ ridge_model_full_data, lasso_model_full_data, elastic_model_full_data, gbr_model_full_data, xgb_model_full_data, lgb_model_full_data, svr_model_full_data, stack_gen_model ] # 分配模型权重 public_coefs = [0.1, 0.1, 0.1, 0.1, 0.15, 0.1, 0.1, 0.25] # 线性融合,取加权平均 def linear_blend_models_predict(data_x,models,coefs, bias): tmp=[model.predict(data_x) for model in models] tmp = [c*d for c,d in zip(coefs,tmp)] pres=np.array(tmp).swapaxes(0,1) pres=np.sum(pres,axis=1) return pres
到这里,房价预测的案例我们就讲解完了,大家可以自己运行一下,看看不同方式训练出来的模型效果。
回顾整个案例会发现,我们在数据预处理和特征工程上花费了很大心思,虽然机器学习问题模型原理比较难学,但实际过程中往往特征工程花费的心思最多。
以上是用Python做一个房价预测小工具!的详细内容。更多信息请关注PHP中文网其他相关文章!




