用 Python 来实现 RSA 加解密

昨天看到一篇英文文章[1]，展示了如何用 Python 来实现 RSA 算法，代码的逻辑与前文一文搞懂 RSA 算法一样，不太熟悉 RSA 的朋友可以看一下一文搞懂 RSA 算法，里面对什么是 RSA，RSA 的数学原理进行了说明，并举了一个简单的例子，可以说是全知乎最容易读懂 RSA 的文章了(这话来自读者评论)。

这篇英文提供的代码我运行了下，发现不能加密中文，于是就修改了下加解密的函数，让其支持中文加解密。今天的文章就分享一下如何用 Python 来实现 RSA 加解密的这一过程，帮助你建立 RSA 的直观认识，代码里的随机素数生成算法，也值得我们学习。

0、效果演示

咱们先看下效果。

原文：“有内鬼，终止交易”

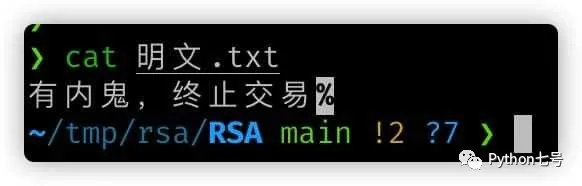
密文，根本无法破解：

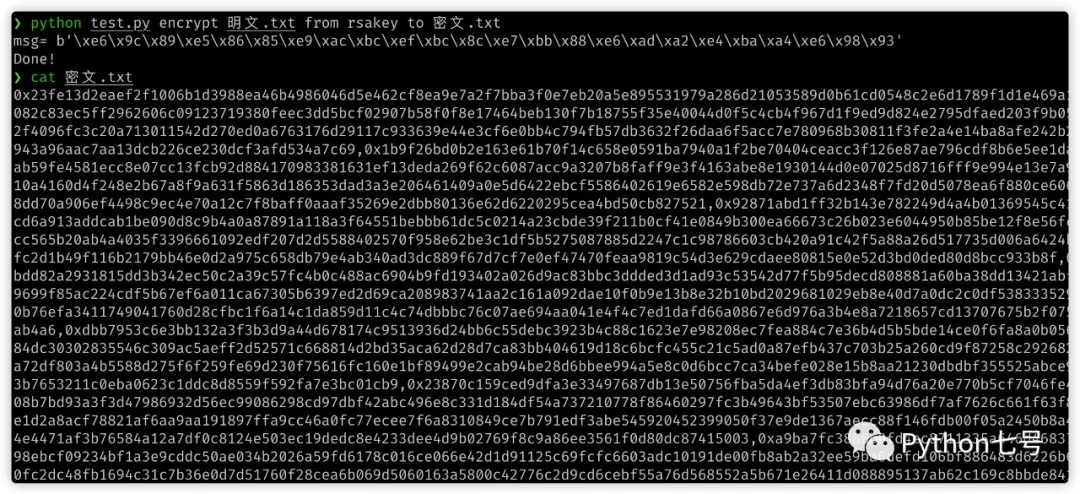
解密之后：

完整代码公众号「Python七号」回复「rsa」获取。

1、密钥对的生成

思路：

1)随机找两个质数(素数) p 和 q，p 与 q 越大，越安全，这里选择 1024 位的质数：

p = genprime(1024)
q = genprime(1024)

genprime() 函数的实现过程先不说。

2)计算他们的乘积 n = p * q 及 欧拉函数 lambda_n。

n = p * q
lambda_n = (p - 1) * (q - 1)

3)随机选择一个整数 e，条件是 1 < e < lambda_n，且 e 与 lambda_n 互质。比如选择 35537，35537 只有 16 位，必然小于 lambda_n。

e = 35537

4)找到一个整数 d，可以使得 e * d 除以 lambda_n 的余数为 1，并返回密钥对。

d = eucalg(e, lambda_n)[0]
if d < 0: d += lambda_n
return (d, n), (e, n)

eucalg 函数的实现放后面说。

至此，密钥对的生成的函数如下：

def create_keys():
 p = genprime(1024)
 q = genprime(1024)
 n = p * q
 lambda_n = (p - 1) * (q - 1)
 e = 35537
 d = eucalg(e, lambda_n)[0]
 if d < 0: d += lambda_n
 return (d, n), (e, n)

2、加解密的实现

加密和解密的过程是一样的，公钥加密，私钥解密，反过来也可以，私钥加密，公钥解密，只不过前者我们叫加密，后者我们叫签名。

具体的函数实现如下：

def encrypt_data(data,key):
e_data = []
for d in data:
 e = modpow(d, key[0], key[1]) 
 e_data.append(e)
return e_data

## 加密和解密的逻辑完全一样
decrypt_data = encrypt_data

这里面用到了 modpow 函数，它用来计算公式 b^e % n = r 的。

• 如果是加密过程，那么 b 是明文，(n,e)为公钥，r 为密文。
• 如果是解密过程，那么 b 是密文，(n,d)为私钥，r 为名文。

modpow 的定义如下：

def modpow(b, e, n):
 # find length of e in bits
 tst = 1
 siz = 0
 while e >= tst:
tst <<= 1
siz += 1
 siz -= 1
 # calculate the result
 r = 1
 for i in range(siz, -1, -1):
r = (r * r) % n
if (e >> i) & 1: r = (r * b) % n
 return r

3、随机质数的生成函数

随机质数的生成函数，其中用到了矩阵乘法和斐波那契数列，可见数学对于算法的重要性。

# matrix multiplication
def sqmatrixmul(m1, m2, w, mod):
 mr = [[0 for j in range(w)] for i in range(w)]
 for i in range(w):
for j in range(w):
 for k in range(w):
mr[i][j] = (mr[i][j] + m1[i][k] * m2[k][j]) % mod
 return mr

# fibonacci calculator
def fib(x, mod):
 if x < 3: return 1
 x -= 2
 # find length of e in bits
 tst = 1
 siz = 0
 while x >= tst:
tst <<= 1
siz += 1
 siz -= 1
 # calculate the matrix
 fm = [
# function matrix
[0, 1],
[1, 1]
 ]
 rm = [
# result matrix
# (identity)
[1, 0],
[0, 1]
 ]
 for i in range(siz, -1, -1):
rm = sqmatrixmul(rm, rm, 2, mod)
if (x >> i) & 1:
 rm = sqmatrixmul(rm, fm, 2, mod)

 # second row of resulting vector is result
 return (rm[1][0] + rm[1][1]) % mod

def genprime(siz):
 while True:
num = (1 << (siz - 1)) + secrets.randbits(siz - 1) - 10;
# num must be 3 or 7 (mod 10)
num -= num % 10
num += 3 # 3 (mod 10)
# heuristic test
if modpow(2, num - 1, num) == 1 and fib(num + 1, num) == 0:
 return num
num += 5 # 7 (mod 10)
# heuristic test
if modpow(2, num - 1, num) == 1 and fib(num + 1, num) == 0:
 return num

4、eucalg 函数的实现

函数的本质在于求下面二元一次方程的解:

e * x - lambda_n * y =1

具体代码：

def eucalg(a, b):
 # make a the bigger one and b the lesser one
 swapped = False
 if a < b:
a, b = b, a
swapped = True
 # ca and cb store current a and b in form of
 # coefficients with initial a and b
 # a' = ca[0] * a + ca[1] * b
 # b' = cb[0] * a + cb[1] * b
 ca = (1, 0)
 cb = (0, 1)
 while b != 0:
# k denotes how many times number b
# can be substracted from a
k = a // b
# swap a and b so b is always the lesser one
a, b, ca, cb = b, a-b*k, cb, (ca[0]-k*cb[0], ca[1]-k*cb[1])
 if swapped:
return (ca[1], ca[0])
 else:
return ca

5、测试

test.py 脚本使用方法：

1）、生成密钥

python test.py make-keys rsakey

公钥保存在 rsakey.pub 中， 私钥保存在 rsakey.priv 中

2）、对文件内容加密

假如有文件 明文.txt：

python test.py encrypt 明文.txt from rsakey to 密文.txt

将生成 密文.txt

3、 对文件内容解密

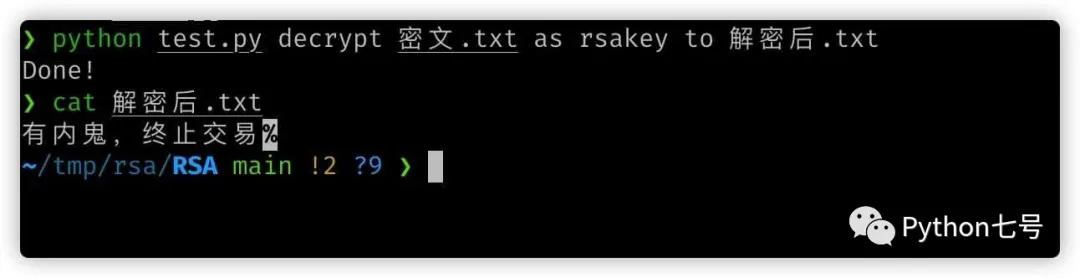
假如有文件 密文.txt：

python test.py decrypt 密文.txt as rsakey to 解密后.txt

将生成 解密后.txt

最后的话

本文分享了 RSA 算法的 Python 的简单实现，可以帮助理解 RSA 算法。

以上是用 Python 来实现 RSA 加解密的详细内容。更多信息请关注PHP中文网其他相关文章！