1994 年，一位数学家想出了如何让量子计算机完成普通经典计算机无法做到的事情。这项工作表明，原则上，一台基于量子力学规则的机器可以有效地将大量数字分解为其主要因素——对于经典计算机而言，这是一项非常困难的任务，它构成了当今大部分互联网安全的基础。
随之而来的是一股乐观情绪。也许，研究人员认为，我们将能够发明可以解决大量不同问题的量子算法。
但进展停滞不前。「这有点令人失望。」卡内基梅隆大学的 Ryan O’Donnell 说，「人们会说，『这太棒了，我相信我们会得到各种其他惊人的算法』，事实是没有。」 科学家们仅在称为 NP 的标准集中发现了单一、狭窄类别问题的显著加速，这意味着他们有有效的可验证解决方案——例如因式分解。
近三年来都是如此。然后在 4 月，研究人员发明了一种全新的问题，量子计算机应该能够比经典计算机更快地解决该问题。它涉及仅基于其混乱的输出来计算复杂数学过程的输入。这个问题是单独存在的，还是许多其他问题中的第一个问题尚待确定。
「有一种兴奋感。」麻省理工学院的计算机科学家 Vinod Vaikuntanathan 说，「很多人都在思考外面还有什么。」
计算机科学家试图通过研究代表它们的数学模型，来了解量子计算机在哪些方面做得更好。通常，他们想象一个量子或经典计算机的模型与称为预言机的理想计算机配对。预言机就像简单的数学函数或计算机程序，接受输入并输出预定的输出。
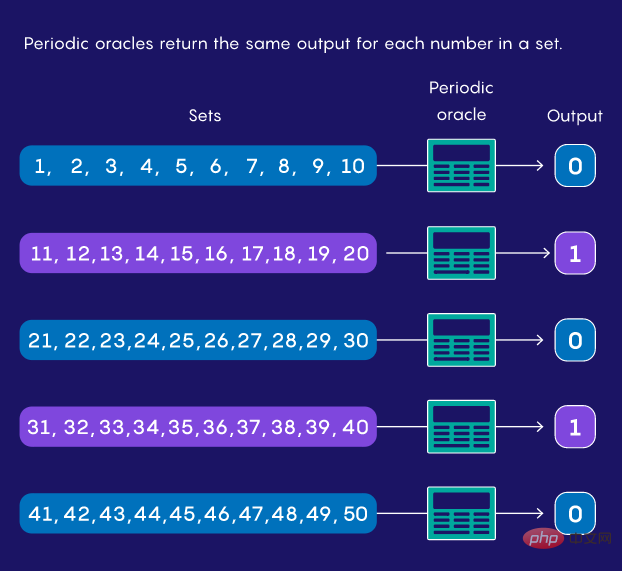
它们可能具有随机行为，如果输入在某个随机范围内（例如，12 到 67）输出「是」，否则输出「否」。或者它们可能是周期性的，因此 1 到 10 之间的输入返回「是」，11 到 20 产生「否」，21 到 30 再次产生「是」，依此类推。
假设您有这些周期性预言之一，但您不知道周期。你所能做的就是给它输入数字，看看它输出了什么。在这些限制条件下，计算机能以多快的速度找到周期？1993 年，当时在蒙特利尔大学的 Daniel Simon 发现，量子算法可以比任何经典算法更快地计算出密切相关问题的答案。
这一结果使 Simon 能够确定量子计算机在哪些方面具有显著优势的最初迹象之一。但是当他将他的论文提交给一个主要会议时，它被拒绝了。然而，这篇论文确实引起了会议项目委员会的一名初级成员——Peter Shor 的兴趣，他当时在新泽西州的贝尔实验室工作。
Shor 继续发现他可以调整 Simon 的算法来计算预言机的周期，如果它有的话。然后他意识到他可以再次调整算法，求解一个行为类似于周期性预言的方程：描述因式分解的方程，它是周期性的。
Shor 的结果是历史性的。他发现的量子算法可以迅速将巨大的数字简化为它们的组成素因数，这是任何已知的经典算法都无法做到的。在随后的几年里，研究人员发现了其他有效的量子算法。其中一些，比如 Shor 的算法，甚至提供了指数优势，但没有人能证明在任何非周期性的 NP 问题上具有显著的量子优势。
由于缺乏进展，德克萨斯大学奥斯汀分校的 Scott Aaronson 和拉脱维亚大学的 Andris Ambainis 两位计算机科学家进行了观察。量子优势的证明似乎总是依赖于具有某种非随机结构的预言，例如周期性。2009 年，他们推测随机或非结构化的 NP 问题不会有显著的加速；谁也找不到例外。
他们的猜想限制了量子计算机的能力。但它只说对于特定类型的非结构化 NP 问题——那些回答是或否的问题——没有显著的加速。如果一个问题涉及找出更具体、定量的答案，也就是所谓的搜索问题，那么这个猜想就不适用了。
考虑到这一点，NTT 社会信息学实验室的研究人员 Takashi Yamakawa 以及 NTT Research 和普林斯顿大学的 Mark Zhandry 决定对一个由 Oded Regev 于 2005 年提出的特定搜索问题进行试验。
想象一组都指向同一个方向的风向标。给他们每个人一个有节制的推，然后让阵风影响他们的方向。Regev 想根据他们的最终方向确定他们最初指向的位置。像这样的问题后来被称为「错误学习」，因为推力和风就像是原始方向上的随机误差源。有证据表明，经典算法和量子算法都很难解决。
Yamakawa 和 Zhandry 调整了设置。他们修改了这些起跑的力量，使它们更容易预测。他们还使风由一个随机的神谕确定，因此在某些情况下它甚至更加随机，但在其他情况下则完全休眠。
通过这些修改，研究人员发现量子算法可以有效地找到初始方向。他们还证明，任何经典算法都必须以指数因子变慢。与 Shor 一样，他们随后调整了算法来解决问题的现实版本，用实际的数学方程代替了预言。
计算机科学家仍在努力理解和解决这个问题。Vaikuntanathan 将其与进行数据压缩时出现的不同情况进行了比较：当信息被压缩时，两个位可能会意外地挤到同一个地方，从而覆盖它们。提前预测这些碰撞以便避免它们的问题有一些相似之处。「这是一类基本上看起来像这样的问题。」他说，「也许这些问题可以在量子上解决。」
人们希望，即使在当今刚刚起步的量子计算机版本上，像新问题这样的非结构化问题也可以解决，从而提供一种测试它们的方法。当时的想法是，非结构化问题可能需要更少的资源来编程，或者对噪声不太敏感，因为它们已经是随机的。但到目前为止，对于现有的量子计算机来说，这个新问题似乎仍然太先进了，无法解决。「这是一个奇怪的问题。我没想过要定义它。」Aaronson 说，「但回想起来，它有一些非常好的功能。」
该结果提供了第一个在非结构化 NP 问题上具有显著量子优势的例子。量子世界会不会有许多其他问题从几乎无法解决变为可以解决？现在有更多的理由这么认为。「这在一定程度上颠覆了我们对量子计算机擅长解决哪些问题的看法。」O’Donnell 说。
以上是量子算法征服了一种新的问题！的详细内容。更多信息请关注PHP中文网其他相关文章！
