二叉搜索树又称二叉排序树，它或者是一棵空树**，或者是具有以下性质的二叉树:
若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树
二叉搜索树的查找类似于二分法查找
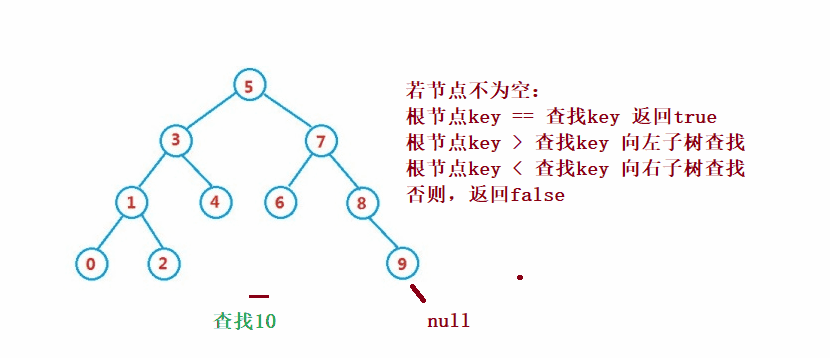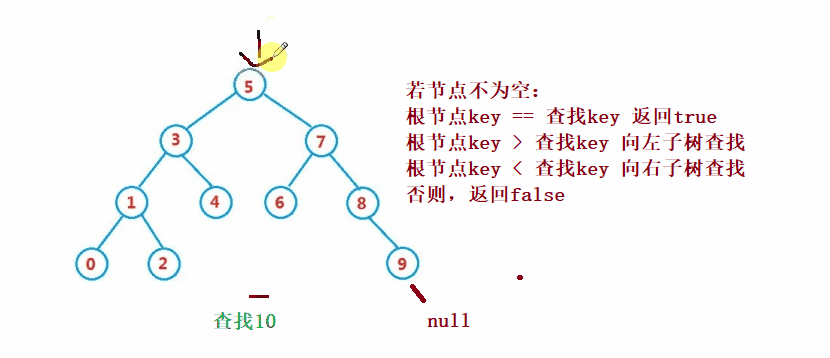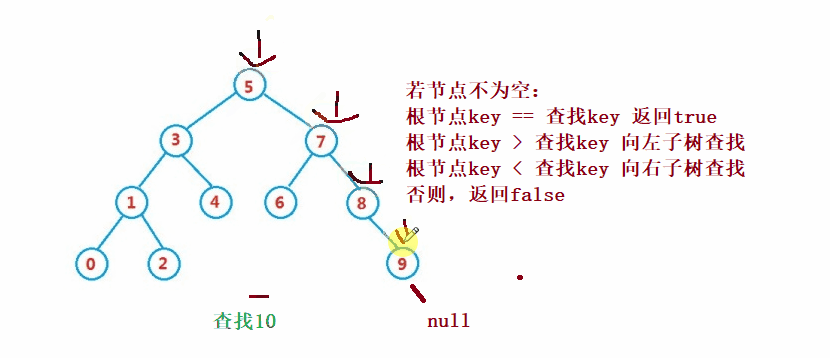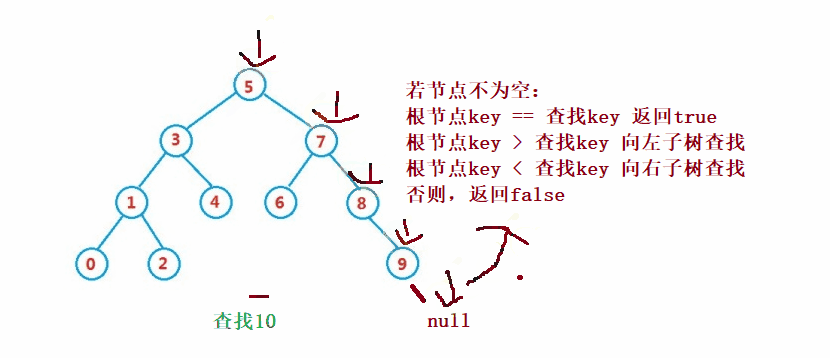
public Node search(int key) {
Node cur = root;
while (cur != null) {
if(cur.val == key) {
return cur;
}else if(cur.val < key) {
cur = cur.right;
}else {
cur = cur.left;
}
}
return null;
}
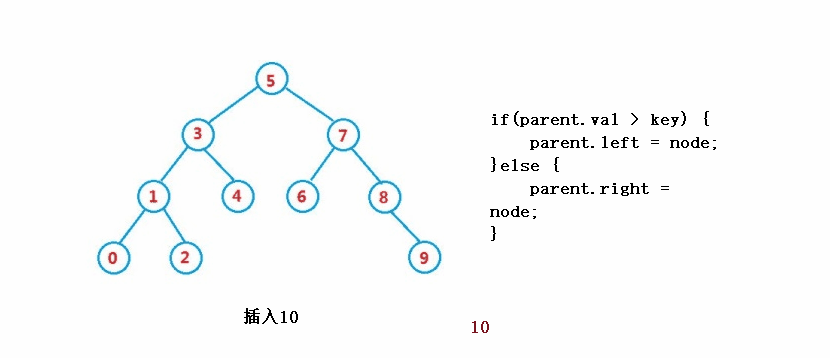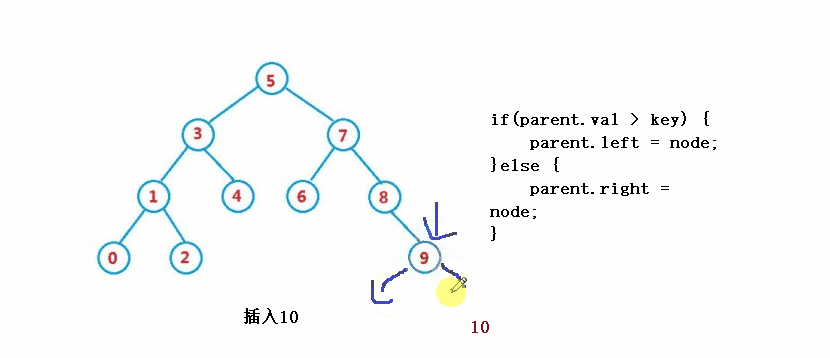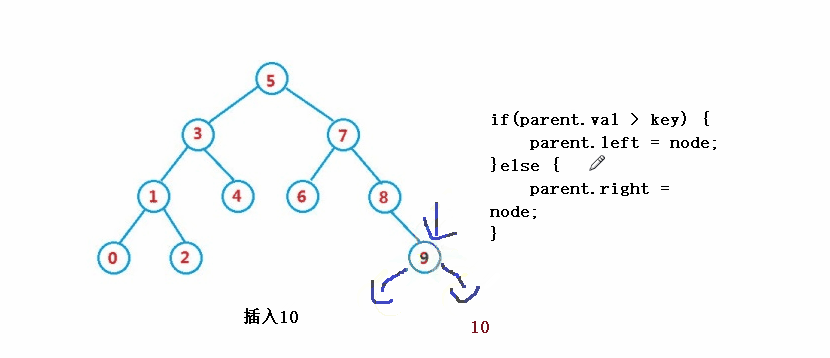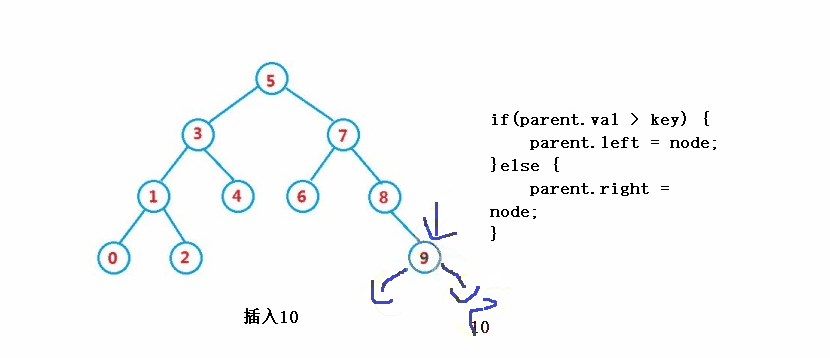
public boolean insert(int key) {
Node node = new Node(key);
if(root == null) {
root = node;
return true;
}
Node cur = root;
Node parent = null;
while(cur != null) {
if(cur.val == key) {
return false;
}else if(cur.val < key) {
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
//parent
if(parent.val > key) {
parent.left = node;
}else {
parent.right = node;
}
return true;
}删除操作较为复杂，但理解了其原理还是比较容易
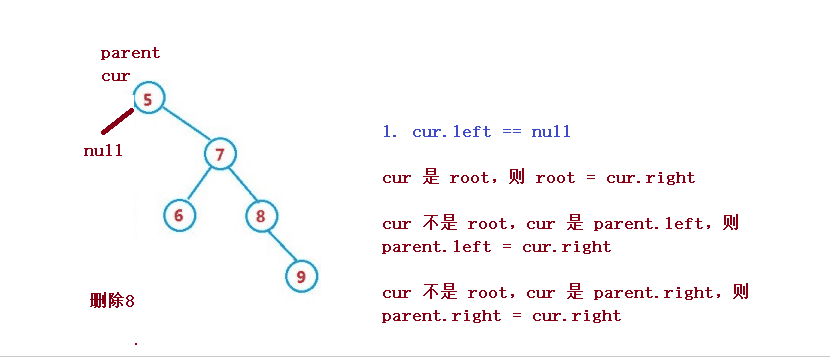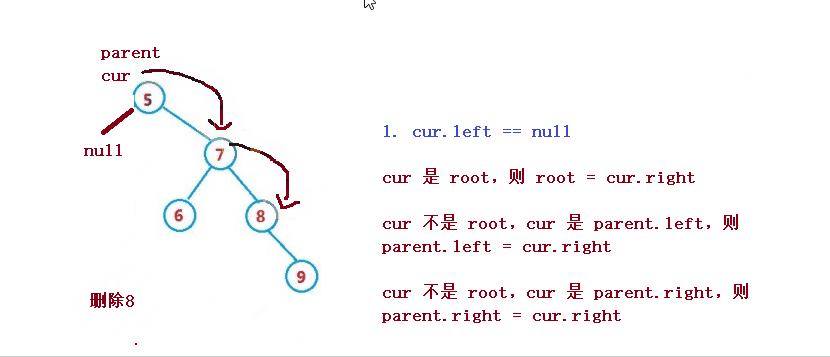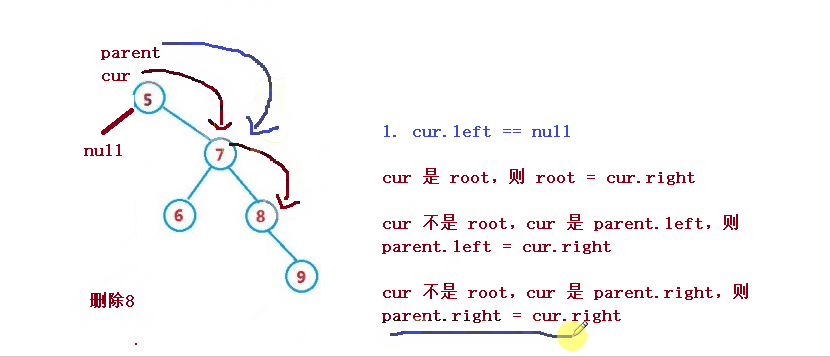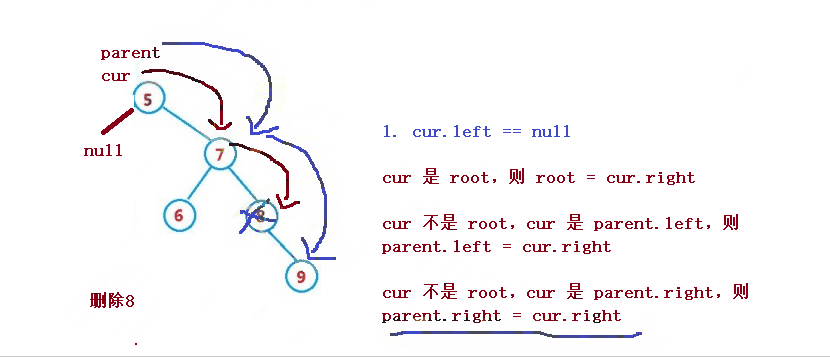
设待删除结点为 cur, 待删除结点的双亲结点为 parent
1. cur 是 root，则 root = cur.right
2. cur 不是 root，cur 是 parent.left，则 parent.left = cur.right
3. cur 不是 root，cur 是 parent.right，则 parent.right = cur.right
1. cur 是 root，则 root = cur.left
2. cur 不是 root，cur 是 parent.left，则 parent.left = cur.left
3. cur 不是 root，cur 是 parent.right，则 parent.right = cur.left
第二种情况和第一种情况相同，只是方向相反，这里不再画图
需要使用替换法进行删除，即在它的右子树中寻找中序下的第一个结点(关键码最小)，用它的值填补到被删除节点中，再来处理该结点的删除问题
当我们在左右子树都不为空的情况下进行删除，删除该节点会破坏树的结构，因此用替罪羊的方法来解决，实际删除的过程还是上面的两种情况，这里还是用到了搜索二叉树的性质
public void remove(Node parent,Node cur) {
if(cur.left == null) {
if(cur == root) {
root = cur.right;
}else if(cur == parent.left) {
parent.left = cur.right;
}else {
parent.right = cur.right;
}
}else if(cur.right == null) {
if(cur == root) {
root = cur.left;
}else if(cur == parent.left) {
parent.left = cur.left;
}else {
parent.right = cur.left;
}
}else {
Node targetParent = cur;
Node target = cur.right;
while (target.left != null) {
targetParent = target;
target = target.left;
}
cur.val = target.val;
if(target == targetParent.left) {
targetParent.left = target.right;
}else {
targetParent.right = target.right;
}
}
}
public void removeKey(int key) {
if(root == null) {
return;
}
Node cur = root;
Node parent = null;
while (cur != null) {
if(cur.val == key) {
remove(parent,cur);
return;
}else if(cur.val < key){
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
}插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二叉搜索树的深度 的函数，即结点越深，则比较次数越多。
但对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树：
最优情况下，二叉搜索树为完全二叉树，其平均比较次数为：
最差情况下，二叉搜索树退化为单支树，其平均比较次数为：
public class TextDemo {
public static class Node {
public int val;
public Node left;
public Node right;
public Node (int val) {
this.val = val;
}
}
public Node root;
/**
* 查找
* @param key
*/
public Node search(int key) {
Node cur = root;
while (cur != null) {
if(cur.val == key) {
return cur;
}else if(cur.val < key) {
cur = cur.right;
}else {
cur = cur.left;
}
}
return null;
}
/**
*
* @param key
* @return
*/
public boolean insert(int key) {
Node node = new Node(key);
if(root == null) {
root = node;
return true;
}
Node cur = root;
Node parent = null;
while(cur != null) {
if(cur.val == key) {
return false;
}else if(cur.val < key) {
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
//parent
if(parent.val > key) {
parent.left = node;
}else {
parent.right = node;
}
return true;
}
public void remove(Node parent,Node cur) {
if(cur.left == null) {
if(cur == root) {
root = cur.right;
}else if(cur == parent.left) {
parent.left = cur.right;
}else {
parent.right = cur.right;
}
}else if(cur.right == null) {
if(cur == root) {
root = cur.left;
}else if(cur == parent.left) {
parent.left = cur.left;
}else {
parent.right = cur.left;
}
}else {
Node targetParent = cur;
Node target = cur.right;
while (target.left != null) {
targetParent = target;
target = target.left;
}
cur.val = target.val;
if(target == targetParent.left) {
targetParent.left = target.right;
}else {
targetParent.right = target.right;
}
}
}
public void removeKey(int key) {
if(root == null) {
return;
}
Node cur = root;
Node parent = null;
while (cur != null) {
if(cur.val == key) {
remove(parent,cur);
return;
}else if(cur.val < key){
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
}
}以上是Java二叉搜索树的增、插、删和创建示例详解的详细内容。更多信息请关注PHP中文网其他相关文章！
