PHP中的动态规划算法详解
PHP中的动态规划算法详解
动态规划(Dynamic Programming)是一种解决问题的算法思想,它通过将问题分解为更小的子问题,并利用已解决的子问题的结果来求解整体问题。在PHP中,动态规划算法可以被广泛应用于许多计算机科学和数学领域,例如最短路径、字符串匹配和背包问题等。本文将详细介绍PHP中的动态规划算法原理,并提供代码示例进行说明。
一、动态规划算法原理
动态规划算法通常包括以下几个步骤:
- 定义问题的状态:将问题划分为较小的子问题,并确定每个子问题的状态。
- 确定状态转移方程:根据子问题的状态,找出子问题之间的递推关系,即状态转移方程。
- 设置边界条件:确定问题的边界条件,即最小子问题的解。
- 递推求解:从最小子问题开始,按照状态转移方程递推求解出最终问题的解。
二、动态规划算法示例
下面以斐波那契数列为例,详细演示PHP中的动态规划算法。
斐波那契数列是指从0开始,第0项是0,第1项是1,从第2项开始,每一项都等于前两项之和。即数列的递推关系为F(n) = F(n-1) + F(n-2),边界条件为F(0) = 0,F(1) = 1。
首先,定义问题的状态,即将斐波那契数列的第n项作为子问题的状态:
function fibonacci($n) {
// 定义状态数组
$dp = array();
// 设置边界条件
$dp[0] = 0;
$dp[1] = 1;
// 递推求解
for ($i = 2; $i <= $n; $i++) {
$dp[$i] = $dp[$i-1] + $dp[$i-2];
}
// 返回结果
return $dp[$n];}
上述代码中,$dp数组用于保存每一项斐波那契数列的值。首先设置边界条件$dp[0] = 0,$dp[1] = 1。然后,通过for循环从第2项开始递推,按照状态转移方程$dp[$i] = $dp[$i-1] + $dp[$i-2]求解出最终问题的解。
通过调用fibonacci函数,可以获取斐波那契数列的第n项的值。例如:
$n = 10;
$result = fibonacci($n);
echo "斐波那契数列第" . $n . "项的值为:" . $result;
运行以上代码,输出结果为:
斐波那契数列第10项的值为:55
三、总结
动态规划是一种重要的算法思想,可以在解决一些复杂问题时提供高效的解决方案。本文以斐波那契数列为例,详细介绍了PHP中的动态规划算法原理,并提供了代码示例进行说明。通过理解动态规划算法的原理和示例,可以更好地应用于实际问题的求解过程中。
以上是PHP中的动态规划算法详解的详细内容。更多信息请关注PHP中文网其他相关文章!

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

热门话题
 适用于 Ubuntu 和 Debian 的 PHP 8.4 安装和升级指南
Dec 24, 2024 pm 04:42 PM
适用于 Ubuntu 和 Debian 的 PHP 8.4 安装和升级指南
Dec 24, 2024 pm 04:42 PM
PHP 8.4 带来了多项新功能、安全性改进和性能改进,同时弃用和删除了大量功能。 本指南介绍了如何在 Ubuntu、Debian 或其衍生版本上安装 PHP 8.4 或升级到 PHP 8.4
 讨论 CakePHP
Sep 10, 2024 pm 05:28 PM
讨论 CakePHP
Sep 10, 2024 pm 05:28 PM
CakePHP 是 PHP 的开源框架。它的目的是使应用程序的开发、部署和维护变得更加容易。 CakePHP 基于类似 MVC 的架构,功能强大且易于掌握。模型、视图和控制器 gu
 如何设置 Visual Studio Code (VS Code) 进行 PHP 开发
Dec 20, 2024 am 11:31 AM
如何设置 Visual Studio Code (VS Code) 进行 PHP 开发
Dec 20, 2024 am 11:31 AM
Visual Studio Code,也称为 VS Code,是一个免费的源代码编辑器 - 或集成开发环境 (IDE) - 可用于所有主要操作系统。 VS Code 拥有针对多种编程语言的大量扩展,可以轻松编写
 CakePHP 快速指南
Sep 10, 2024 pm 05:27 PM
CakePHP 快速指南
Sep 10, 2024 pm 05:27 PM
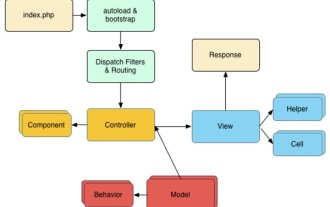
CakePHP 是一个开源MVC 框架。它使开发、部署和维护应用程序变得更加容易。 CakePHP 有许多库可以减少大多数常见任务的过载。
 您如何在PHP中解析和处理HTML/XML?
Feb 07, 2025 am 11:57 AM
您如何在PHP中解析和处理HTML/XML?
Feb 07, 2025 am 11:57 AM
本教程演示了如何使用PHP有效地处理XML文档。 XML(可扩展的标记语言)是一种用于人类可读性和机器解析的多功能文本标记语言。它通常用于数据存储