在Java中的记忆化（1D，2D和3D）动态规划-java教程-PHP中文网

1-D记忆化

示例

输出

n=5的斐波那契值为：5

n=5时的斐波那契值为：5

2-D Memorization

方法

三维记忆化

首页

Java

java教程

在Java中的记忆化（1D，2D和3D）动态规划

WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB

Aug 23, 2023 pm 02:13 PM

java 记忆化动态规划

记忆化是一种基于动态规划的技术，用于通过确保方法不会对相同的输入集合运行多次来改进递归算法的性能，通过记录提供的输入的结果（存储在数组中）。可以通过实现递归方法的自顶向下的方法来实现记忆化。

让我们通过基本的斐波那契数列示例来理解这种情况。

1-D记忆化

我们将考虑一个只有一个非常量参数（只有一个参数的值发生变化）的递归算法，因此这个方法被称为1-D记忆化。以下代码是用于找到斐波那契数列中第N个（所有项直到N）的。

示例

public int fibonacci(int n) {
   if (n == 0)
      return 0;
   if (n == 1)
      return 1;
   System.out.println("Calculating fibonacci number for: " + n);
   return (fibonacci(n - 1) + fibonacci(n - 2));
}

登录后复制

输出

如果我们使用n=5运行上述代码，将会生成以下输出。

Calculating fibonacci number for: 5
Calculating fibonacci number for: 4
Calculating fibonacci number for: 3
Calculating fibonacci number for: 2
Calculating fibonacci number for: 2
Calculating fibonacci number for: 3
Calculating fibonacci number for: 2

登录后复制

n=5的斐波那契值为：5

注意到对于2和3的斐波那契数被计算了多次。让我们通过绘制上述条件n=5的递归树来更好地理解。

在节点的两个子节点将表示它所做的递归调用。可以看到F(3)和F(2)被计算了多次，可以通过在每一步之后缓存结果来避免。

我们将使用一个实例变量memoize Set来缓存结果。首先检查memoize Set中是否已经存在n，如果是，则返回该值；如果不是，则计算该值并添加到集合中。

示例

import java.util.HashMap;
import java.util.Map;
public class TutorialPoint {
   private Map<Integer, Integer> memoizeSet = new HashMap<>(); // O(1)
   public int fibMemoize(int input) {
      if (input == 0)
         return 0;
      if (input == 1)
         return 1;
      if (this.memoizeSet.containsKey(input)) {
         System.out.println("Getting value from computed result for " + input);
         return this.memoizeSet.get(input);
      }
      int result = fibMemoize(input - 1) + fibMemoize(input - 2);
      System.out.println("Putting result in cache for " + input);
      this.memoizeSet.put(input, result);
      return result;
   }
   public int fibonacci(int n) {
      if (n == 0)
         return 0;
      if (n == 1)
         return 1;
      System.out.println("Calculating fibonacci number for: " + n);
      return (fibonacci(n - 1) + fibonacci(n - 2));
   }
   public static void main(String[] args) {
      TutorialPoint tutorialPoint = new TutorialPoint();
      System.out.println("Fibonacci value for n=5: " + tutorialPoint.fibMemoize(5));
   }
}

登录后复制

输出

如果我们运行上述代码，将会生成以下输出

Adding result in memoizeSet for 2
Adding result in memoizeSet for 3
Getting value from computed result for 2
Adding result in memoizeSet for 4
Getting value from computed result for 3
Adding result in memoizeSet for 5

登录后复制

n=5时的斐波那契值为：5

从上面可以看出，2和3的斐波那契数不会再次计算。在这里，我们引入了一个HashMap memorizes来存储已经计算过的值，在每次斐波那契计算之前，检查集合中是否已经计算了输入的值，如果没有，则将特定输入的值添加到集合中。

2-D Memorization

在上面的程序中，我们只有一个非常数参数。在下面的程序中，我们将以递归程序为例，该程序具有两个参数，在每次递归调用后更改其值，并且我们将在两个非常数参数上实现记忆化以进行优化。这被称为2-D记忆化。

例如：我们将实现标准的最长公共子序列(LCS)。如果给定一组序列，则最长公共子序列问题是找到所有序列的共同子序列，该子序列的长度最大。可能的组合将有2^n个。

示例

class TP {
   static int computeMax(int a, int b) {
      return (a > b) ? a : b;
   }
   static int longestComSs(String X, String Y, int m, int n) {
      if (m == 0 || n == 0)
         return 0;
      if (X.charAt(m - 1) == Y.charAt(n - 1))
         return 1 + longestComSs(X, Y, m - 1, n - 1);
      else
         return computeMax(longestComSs(X, Y, m, n - 1), longestComSs(X, Y, m - 1, n));
   }
   public static void main(String[] args) {
      String word_1 = "AGGTAB";
      String word_2 = "GXTXAYB";
      System.out.print("Length of LCS is " + longestComSs(word_1, word_2, word_1.length(),word_2.length()));
   }
}

登录后复制

输出

如果我们运行上述代码，将会生成以下输出

Length of LCS is 4

登录后复制

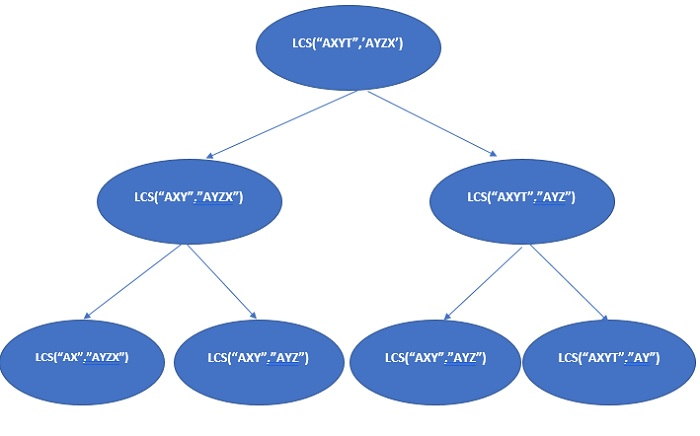
在Java中的记忆化（1D，2D和3D）动态规划

在上述的递归树中，lcs("AXY", "AYZ") 被解决了多次。

由于这个问题具有重叠子结构的特性，可以通过使用记忆化或表格化来避免对相同子问题的重复计算。

递归代码的记忆化方法实现如下。

示例

import java.io.*;
import java.lang.*;
class testClass {
   final static int maxSize = 1000;
   public static int arr[][] = new int[maxSize][maxSize];
   public static int calculatelcs(String str_1, String str_2, int m, int n) {
      if (m == 0 || n == 0)
         return 0;
      if (arr[m - 1][n - 1] != -1)
         return arr[m - 1][n - 1];
      if (str_1.charAt(m - 1) == str_2.charAt(n - 1)) {
         arr[m - 1][n - 1] = 1 + calculatelcs(str_1, str_2, m - 1, n - 1);
         return arr[m - 1][n - 1];
      }
      else {
         int a = calculatelcs(str_1, str_2, m, n - 1);
         int b = calculatelcs(str_1, str_2, m - 1, n);
         int max = (a > b) ? a : b;
         arr[m - 1][n - 1] = max;
         return arr[m - 1][n - 1];
      }
   }
   public static void main(String[] args) {
      for (int i = 0; i < 1000; i++) {
         for (int j = 0; j < 1000; j++) {
            arr[i][j] = -1;
         }
      }
      String str_1 = "AGGTAB";
      String str_2 = "GXTXAYB";
      System.out.println("Length of LCS is " + calculatelcs(str_1, str_2, str_1.length(),str_2.length()));
   }
}

登录后复制

输出

如果我们运行上述代码，将会生成以下输出

Length of LCS is 4

登录后复制

方法

观察到在方法(calculatelcs)中有4个参数，其中有2个常数（不影响记忆化），还有2个非常数参数(m和n)，在每次递归调用方法时会改变其值。为了实现记忆化，我们引入一个二维数组来存储计算过的lcs(m,n)的值，存储在arr[m-1][n-1]中。当再次调用具有相同参数m和n的函数时，我们不再执行递归调用，而是直接返回arr[m-1][n-1]，因为之前计算的lcs(m, n)已经存储在arr[m-1][n-1]中，从而减少了递归调用的次数。

三维记忆化

这是一种用于具有3个非常数参数的递归程序的记忆化方法。在这里，我们以计算三个字符串的LCS长度为例。

这里的方法是生成给定字符串的所有可能子序列（总共可能的子序列有3ⁿ个），并在其中匹配最长的公共子序列。

我们将引入一个三维表来存储计算过的值。考虑到子序列。

A1[1...i] i < N
A2[1...j] j < M
A3[1...k] k < K

如果我们找到一个公共字符(X[i]==Y[j]==Z[k])，我们需要递归处理剩余的字符。否则，我们将计算以下情况的最大值

保留X[i]递归处理其他字符
保留Y[j]递归处理其他字符
保留Z[k]递归处理其他字符

因此，如果我们将上述想法转化为递归函数，则

f(N,M,K)={1+f(N-1,M-1,K-1)if (X[N]==Y[M]==Z[K]maximum(f(N-1,M,K),f(N,M-1,K),f(N,M,K-1))}

f(N-1,M,K) = 保留X[i]递归处理其他字符
f(N,M-1,K) = 保留Y[j]递归处理其他字符
f(N,M,K-1) = 保留Z[k]递归处理其他字符

示例

import java.io.IOException;
import java.io.InputStream;
import java.util.*;
class testClass {
   public static int[][][] arr = new int[100][100][100];
   static int calculatelcs(String str_1, String str_2, String str_3, int m, int n, int o) {
         for (int i = 0; i <= m; i++) {
            for (int j = 0; j <= n; j++) {
               arr[i][j][0] = 0;
            }
         }
         for (int i = 0; i <= n; i++) {
            for (int j = 0; j <= o; j++) {
               arr[0][i][j] = 0;
            }
         }
         for (int i = 0; i <= m; i++) {
            for (int j = 0; j <= o; j++) {
               arr[i][0][j] = 0;
            }
         }
         for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
               for (int k = 1; k <= o; k++) {
                  if (str_1.charAt(i - 1) == str_2.charAt(j-1) && str_2.charAt(j1) == str_3.charAt(k-1)) {
                     arr[i][j][k] = 1 + arr[i - 1][j - 1][k - 1];
                  }
                  else {
                     arr[i][j][k] = calculateMax(arr[i - 1][j][k], arr[i][j - 1][k], arr[i][j][k - 1]);
                  }
               }
            }
         }
         return arr[m][n][o];
   }
   static int calculateMax(int a, int b, int c) {
      if (a > b && a > c)
         return a;
         if (b > c)
         return b;
         return c;
   }
   public static void main(String[] args) {
      String str_1 = "clued";
      String str_2 = "clueless";
      String str_3 = "xcxclueing";
      int m = str_1.length();
      int n = str_2.length();
      int o = str_3.length();
      System.out.print("Length of LCS is " + calculatelcs(str_1, str_2, str_3, m, n, o));
   }
}

登录后复制