使用归并排序算法编写的C/C++程序,用于计算数组中的逆序数

数组的反转表示;需要进行多少次更改才能将数组转换为其排序形式。当数组已经排序时,需要 0 次反转,而在其他情况下,如果数组反转,反转次数将达到最大。
为了解决这个问题,我们将遵循归并排序方法降低时间复杂度,采用分治算法。
输入
A sequence of numbers. (1, 5, 6, 4, 20).
输出
将数字升序排列所需的反转次数。
Here the number of inversions are 2. First inversion: (1, 5, 4, 6, 20) Second inversion: (1, 4, 5, 6, 20)
算法
merge(array, tempArray, left, mid, right)
输入 - 两个数组,谁已经合并,左,右和中间索引。
输出-按排序顺序合并的数组。
Begin
i := left, j := mid, k := right
count := 0
while i <= mid -1 and j <= right, do
if array[i] <= array[j], then
tempArray[k] := array[i]
increase i and k by 1
else
tempArray[k] := array[j]
increase j and k by 1
count := count + (mid - i)
done
while left part of the array has some extra element, do
tempArray[k] := array[i]
increase i and k by 1
done
while right part of the array has some extra element, do
tempArray[k] := array[j]
increase j and k by 1
done
return count
EndmergeSort(array, tempArray, left, right)
输入 - 给定数组和临时数组,数组的左右索引。
输出 - 排序后的逆序对数量。
Begin
count := 0
if right > left, then
mid := (right + left)/2
count := mergeSort(array, tempArray, left, mid)
count := count + mergeSort(array, tempArray, mid+1, right)
count := count + merge(array, tempArray, left, mid+1, right)
return count
End示例
实时演示
#include <iostream>
using namespace std;
int merge(int arr[], int temp[], int left, int mid, int right) {
int i, j, k;
int count = 0;
i = left; //i to locate first array location
j = mid; //i to locate second array location
k = left; //i to locate merged array location
while ((i <= mid - 1) && (j <= right)) {
if (arr[i] <= arr[j]){ //when left item is less than right item
temp[k++] = arr[i++];
} else {
temp[k++] = arr[j++];
count += (mid - i); //find how many convertion is performed
}
}
while (i <= mid - 1) //if first list has remaining item, add them in the list
temp[k++] = arr[i++];
while (j <= right) //if second list has remaining item, add them in the list
temp[k++] = arr[j++];
for (i=left; i <= right; i++)
arr[i] = temp[i]; //store temp Array to main array
return count;
}
int mergeSort(int arr[], int temp[], int left, int right){
int mid, count = 0;
if (right > left) {
mid = (right + left)/2; //find mid index of the array
count = mergeSort(arr, temp, left, mid); //merge sort left sub array
count += mergeSort(arr, temp, mid+1, right); //merge sort right sub array
count += merge(arr, temp, left, mid+1, right); //merge two sub arrays
}
return count;
}
int arrInversion(int arr[], int n) {
int temp[n];
return mergeSort(arr, temp, 0, n - 1);
}
int main() {
int arr[] = {1, 5, 6, 4, 20};
int n = 5;
cout << "Number of inversions are "<< arrInversion(arr, n);
}输出
Number of inversions are 2
以上是使用归并排序算法编写的C/C++程序,用于计算数组中的逆序数的详细内容。更多信息请关注PHP中文网其他相关文章!

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

热门话题
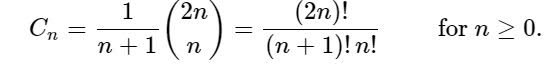 第n个卡塔兰数的C/C++程序是什么?
Sep 11, 2023 pm 10:33 PM
第n个卡塔兰数的C/C++程序是什么?
Sep 11, 2023 pm 10:33 PM
卡塔兰数是一系列数字。卡塔兰数是一系列自然数,在各种计数问题中出现,通常涉及递归定义的对象。Cn是长度为2n的Dyck词的数量。Dyck词是由n个X和n个Y组成的字符串,使得字符串的任何初始片段中Y的数量不超过X的数量。例如,以下是长度为6的Dyck词:XXXYYYXYXXYYXYXYXYXXYYXYXXYXYY.将符号X重新解释为开括号,将Y解释为闭括号,Cn计算包含n对正确匹配的括号的表达式的数量((()))()(())()()()(())()(()())Cn是n+1个因子可以完全括起来的不
 使用归并排序算法编写的C/C++程序,用于计算数组中的逆序数
Aug 25, 2023 pm 07:33 PM
使用归并排序算法编写的C/C++程序,用于计算数组中的逆序数
Aug 25, 2023 pm 07:33 PM
数组的反转表示;需要进行多少次更改才能将数组转换为其排序形式。当数组已经排序时,需要0次反转,而在其他情况下,如果数组反转,反转次数将达到最大。为了解决这个问题,我们将遵循归并排序方法降低时间复杂度,采用分治算法。输入Asequenceofnumbers.(1,5,6,4,20).输出将数字升序排列所需的反转次数。Herethenumberofinversionsare2.Firstinversion:(1,5,4,6,20)Secondinversion:(1,4,5,6,20)算法merge
 php怎么实现并归排序
Oct 21, 2022 am 09:30 AM
php怎么实现并归排序
Oct 21, 2022 am 09:30 AM
php实现并归排序的方法:1、创建一个PHP示例文件;2、定义“public function handle(){...}”方法;3、通过“private function mergeSort($a, $lo, $hi) {...}”方法把数据逐步分解;4、通过“merge”方法对分解后的数据进行排序,再合并到一起即可。
 PHP中的归并排序算法详解
Jul 08, 2023 pm 05:03 PM
PHP中的归并排序算法详解
Jul 08, 2023 pm 05:03 PM
PHP中的归并排序算法详解引言:排序是计算机科学中常见的基本问题之一,对于数据的有序排列可以提高检索、查找和修改等操作的效率。在排序算法中,归并排序是一种效率较高且稳定的算法。本文将详细介绍PHP中的归并排序算法,并附带代码示例。归并排序的原理归并排序是一种分治算法,它将待排序的数组分成两个子数组,分别对这两个子数组进行归并排序,然后将已排序的子数组合并成一
 如何实现C#中的归并排序算法
Sep 19, 2023 am 09:45 AM
如何实现C#中的归并排序算法
Sep 19, 2023 am 09:45 AM
如何实现C#中的归并排序算法归并排序是一种基于分治思想的经典排序算法,其通过将一个大问题划分为多个小问题、然后逐步解决小问题并合并结果来完成排序。下面将介绍如何在C#中实现归并排序算法,并提供具体的代码示例。归并排序的基本思想是将待排序的序列拆分为多个子序列,分别进行排序,然后再将排序好的子序列合并成一个有序的序列。该算法的关键是实现子序列的拆分和合并操作。
 将C/C++程序转换为预处理器代码
Sep 11, 2023 pm 04:21 PM
将C/C++程序转换为预处理器代码
Sep 11, 2023 pm 04:21 PM
这里我们将看到如何从C或C++程序的源代码生成预处理或预处理器代码。要使用g++编译器查看预处理代码,我们必须使用'-E'选项与g++。预处理器包含代码中的所有#指令,并且还扩展了MACRO函数。语法g++-Eprogram.cpp示例#define PI 3.1415int main() { float a = PI,&nb
 如何使用java实现归并排序算法
Sep 19, 2023 am 11:33 AM
如何使用java实现归并排序算法
Sep 19, 2023 am 11:33 AM
如何使用Java实现归并排序算法引言:归并排序是一种基于分治法的经典排序算法,其思想是将待排序的数组逐层划分为更小的子数组,然后通过合并操作依次将子数组有序地合并成一个有序的整体数组。在本篇文章中,我们将详细介绍如何使用Java实现归并排序算法,并提供具体的代码示例。算法步骤:归并排序算法主要包括三个步骤:拆分、合并和排序。拆分(Split):首先,我们需要
 如何使用分治法在PHP中实现归并排序算法并提高排序效率?
Sep 19, 2023 pm 02:10 PM
如何使用分治法在PHP中实现归并排序算法并提高排序效率?
Sep 19, 2023 pm 02:10 PM
如何使用分治法在PHP中实现归并排序算法并提高排序效率?归并排序是一种高效的排序算法,它采用分治法的思想将待排序的数组分成两个部分,分别对这两个子数组进行排序,然后再将两个已排序的子数组合并成一个有序的数组。通过不断地将问题分解为更小的子问题,并将子问题的解合并起来,归并排序能够稳定地将一个未排序的数组变成有序的数组。在PHP中,实现归并排序算法并提高排序效






