具有最多M个连续节点且值为K的从根到叶子的路径数量
简介
二叉树是一种令人着迷的数据结构,在计算机科学和编程中有着广泛的应用。一个有趣的问题是从给定的由父节点及其子节点组成的树中查找计数。二叉树由节点组成,根节点确定,根节点可以根据用户需要给出子节点。 K值决定,移动方式由M值选择。
根到叶路径的计数
该图是使用各种节点创建的,这些节点保存整数形式的值。本文主要关注从起始节点或根节点到叶子节点或子节点的计数。
示例
该图是从具有各种节点的二叉树创建的。
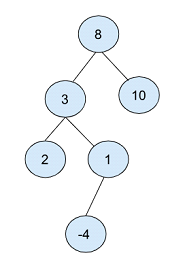
在上面的二叉树中,根节点选择为“8”。
然后创建两个节点,一个值为 3,另一个值为 10,占据根节点的左右位置。
以值为 2 的节点作为根,创建另一个子节点,其值分别为 2 和 1 作为左节点和右节点。
最后,值为 1 的子节点创建值为 -4 的子节点。
方法 1:使用递归函数计算由最多 M 个具有 K 值的连续节点组成的根到叶路径的 C++ 代码
为了有效地解决这个问题,我们将利用树遍历算法和递归等基本概念。
算法
第 1 步:创建一个用于表示树节点的结构,其中包括两个指针(左子节点和右子节点)以及用于存储节点值的整数字段。
第 2 步:设计一个递归函数,从根开始遍历二叉树,同时跟踪当前路径长度(初始化为 0)、连续出现次数(初始设置为 0)、目标值 K,允许的最大连续出现次数 M。
第 3 步:在每个左子树和右子树上递归调用该函数,并传递更新的参数,例如递增的路径长度和连续出现次数(如果适用)。
第4步:对于遍历过程中每个访问过的非空节点:
a) 如果其值等于 K,则将两个变量都加一。
b) 如果其值与 K 不匹配或超过迄今为止在路径中已遇到的 M 连续出现次数,则将变量重置为零。
第5步:在遍历树时,如果子节点在左和右两种情况下的值都为零 - 我们可以用两种方式处理,即
a) 检查变量是否不超过M。
b) 如果是,则将满足条件的路径总数增加 1。
示例
//including the all in one header
#include<bits/stdc++.h>
using namespace std;
//creating structure with two pointers as up and down
struct Vertex {
int data;
struct Vertex* up;
struct Vertex* down;
};
//countPaths function declared with five arguments ; with root = end; Node= vertex; left = up; right = down
int countPaths(Vertex* end, int K, int M, int currCount, int
consCount) {
//To check the condition when the root is equal to 1 and greater than the maximum value, the values is incremented
if (end == NULL || consCount > M) {
return 0;
}
//To check when the root is equal to the K value, increment by 1
if (end->data == K) {
currCount++;
consCount++;
} else {
//If it is not equal, it will return 0
currCount = 0;
}
if (end->up == NULL && end->down == NULL) {
if (currCount <= M) {
return 1;
} else {
return 0;
}
}
return countPaths(end->up, K, M, currCount, consCount) + countPaths(end->down, K, M, currCount, consCount);
}
//Main function to test the implementation
int main() {
Vertex* end = new Vertex();
end->data = 8;
end->up = new Vertex();
end->up->data = 3;
end->down = new Vertex();
end->down->data = 10;
end->up->up = new Vertex();
end->up->up->data = 2;
end->up->down = new Vertex();
end->up->down->data = 1;
end->up->down->up = new Vertex();
end->up->down->up->data = -4;
int K = 1; // Value of node
int M = 2; // Maximum consecutive nodes
int currCount = -1; // Current count
int consCount = -1; // Consecutive count
cout << "The number of paths obtained from the given graph of" << M << "nodes with a value of " << K << " is " << countPaths(end, K, M, currCount, consCount) << endl;
return 0;
}
输出
The number of paths obtained from the given graph of 2 nodes with a value of 1 is 3
结论
在本文中,我们探讨了计算从顶部(即叶)到末端或根的路径数的问题。通过使用 C++ 中的树遍历算法和递归技术,可以有效地解决此类问题。遍历二叉树的过程看起来很困难,但通过示例就变得简单了。
以上是具有最多M个连续节点且值为K的从根到叶子的路径数量的详细内容。更多信息请关注PHP中文网其他相关文章!

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

热门话题
 什么是MD5哈希值?
Feb 18, 2024 pm 08:50 PM
什么是MD5哈希值?
Feb 18, 2024 pm 08:50 PM
MD5值是什么?在计算机科学中,MD5(MessageDigestAlgorithm5)是一种常用的散列函数,用于对消息进行摘要或加密。它产生一个固定长度的128位二进制数字,通常以32位的十六进制表示。MD5算法由RonaldRivest于1991年设计。尽管在密码学领域中,MD5算法被认为已经不再安全,但它仍广泛应用于数据完整性验证和文件校验等方
 PHP值解析:详解PHP中值的概念及应用
Mar 21, 2024 pm 09:06 PM
PHP值解析:详解PHP中值的概念及应用
Mar 21, 2024 pm 09:06 PM
PHP值解析:详解PHP中值的概念及应用在PHP编程中,值是一个非常基础且重要的概念。在本文中,我们将深入探讨PHP中值的概念及其在实际编程中的应用。我们将从基本值类型,变量,数组,对象和常量等方面进行详细解析,并提供具体的代码示例,帮助读者更好地理解和运用PHP中的值。基本值类型在PHP中,最常见的基本值类型包括整型,浮点型,字符串,布尔型和空值。这些基本
 探讨Go语言中不可寻址的值
Mar 25, 2024 am 09:33 AM
探讨Go语言中不可寻址的值
Mar 25, 2024 am 09:33 AM
在Go语言中,有一些值是不可寻址的,即无法取得它们的内存地址。这些值包括常量、字面量和不能被取地址的表达式。在本文中,我们将探讨这些不可寻址的值,并通过具体的代码示例来理解它们的特性。首先,我们来看一些常量的例子。在Go语言中,常量是不可寻址的,因为常量是在编译时就确定其值的,不存在运行时的内存地址可供访问。下面是一个示例代码:packagemaini
 使用C++编程,找到在网格中从一个点到另一个点的路径数量
Aug 29, 2023 pm 10:25 PM
使用C++编程,找到在网格中从一个点到另一个点的路径数量
Aug 29, 2023 pm 10:25 PM
在本文中,我们给出了一个问题,我们需要找到从点A到点B的总路径数,其中A和B是固定点,即A是网格中的左上角点,B是网格中的右下角点,例如−Input:N=5Output:252Input:N=4Output:70Input:N=3Output:20在给定的问题中,我们可以通过简单的观察来形式化答案并得出结果。寻找解决方案的方法在这种方法中,我们通过观察得出一个公式,即从A到B穿过网格时,我们需要向右行进n次,向下行进n次,这意味着我们需要找到所有可能的路径组合,因此我们得到了
 Java 8中的Optional类:如何使用filter()方法过滤可能为空的值
Aug 01, 2023 pm 05:27 PM
Java 8中的Optional类:如何使用filter()方法过滤可能为空的值
Aug 01, 2023 pm 05:27 PM
Java8中的Optional类:如何使用filter()方法过滤可能为空的值在Java8中,Optional类是一个非常有用的工具,它允许我们更好地处理可能为空的值,避免了NullPointerException的发生。Optional类提供了许多方法来操作潜在的空值,其中一个重要的方法是filter()。filter()方法的作用是,如果Option
 使用C++找到K叉树中权重为W的路径数量
Sep 16, 2023 pm 06:09 PM
使用C++找到K叉树中权重为W的路径数量
Sep 16, 2023 pm 06:09 PM
在本文中,我们将使用C++来计算K叉树中权重为W的路径数量。我们已经给出了一个K叉树,它是一棵每个节点有K个子节点且每条边都有一个权重的树,权重从1到K递减从一个节点到其所有子节点。我们需要计算从根节点开始的累积路径数量,这些路径具有权重为W且至少有一条边的权重为M。所以,这是一个例子:Input:W=4,K=3,M=2Output:6在给定的问题中,我们将使用dp来减少时间和空间复杂度。通过使用记忆化,我们可以使我们的程序更快,并使其适用于更大的约束。方法在这个方法中,我们将遍历树,并跟踪使用
 探索Java Map的魅力,破解数据处理的难题
Feb 19, 2024 pm 07:03 PM
探索Java Map的魅力,破解数据处理的难题
Feb 19, 2024 pm 07:03 PM
Map的讲解Map是一种数据结构,允许你存储键值对,键是唯一的,值可以是任何类型的对象。Map接口提供了存储和检索键值对的方法,以及允许你遍历Map中的键值对。Map的类型Java中Map有几种不同的实现,最常见的是HashMap、TreeMap和LinkedHashMap。HashMap:一个基于散列表的Map实现,具有快速查找、插入和删除的特点,但它不是有序的,这意味着键值对的顺序在Map中是任意决定的。TreeMap:一个基于红黑树的Map实现,具有快速查找、插入和删除的特点,并且它是带有
 当在JavaScript中将某个值转换为布尔值时会发生什么?
Sep 02, 2023 am 09:21 AM
当在JavaScript中将某个值转换为布尔值时会发生什么?
Sep 02, 2023 am 09:21 AM
使用JavaScript中的Boolean()方法转换为布尔值。您可以尝试运行以下代码来了解如何在JavaScript中将[50,100]转换为布尔值。示例实时演示<!DOCTYPEhtml><html> <body> <p>Convert[50,100]toBoolean</p> &






