使用C++找出在第L个和第R个索引之间只有设置位的数字

在给定的问题中,我们需要找到一个数字的值,该数字在给定的范围L、R之间具有所有的设置位。例如 −
Input: L = 1, R = 5 Output: 62 Explanation: representation of given L and R in binary form is 0..0111110 Input: L = 1, R = 4 Output: 30 Explanation: representation of given L and R in binary form is 0..11110
找到解决方案的方法
在给定的问题中,我们将讨论两种方法,暴力法和高效方法。
暴力法
在这种方法中,我们只需遍历给定的范围,并将给定范围内的所有2的幂相加,这将是我们的答案。
示例
#include<bits/stdc++.h>
using namespace std;
int main() {
int L = 1, R = 3; // the given range
int ans = 0; // our answer
for(int i = L; i <= R; i++) // traversing through the whole range
ans += pow(2, i); // adding values to the answer.
cout << ans << "\n";
}输出
14
在这种方法中,我们只是遍历范围并简单地将范围内的数字的2的幂相加。这个程序的时间复杂度为O(N),其中N是我们范围的大小。但是我们可以通过应用给定问题中的位知识进一步改进时间复杂度。
高效的方法
在这种方法中,我们将简单地构造一个公式来计算我们的答案。
示例
#include<bits/stdc++.h>
using namespace std;
int main() {
int L = 1, R = 3; // the given range
int ans = 0; // our answer
for(int i = L; i <= R; i++) // traversing through the whole range
ans += pow(2, i); // adding values to the answer.
cout << ans << "\n";
}输出
14
在这种方法中,我们制定了一个计算答案的公式。
上述代码的解释
正如您所知,我们需要计算给定范围内具有设置位的数字,因此在这种方法中,我们找到一个从0到R的所有位都设置的数字。然后我们需要从1到(L-1)中减去一个所有位都设置的数字,因此我们制定了这个观察结果。给定代码的总体时间复杂度为O(1),即常数时间复杂度,这意味着我们可以在常数时间内计算任何答案。
结论
本文将为“仅在L-th和R-th索引之间具有设置位的数字”编写一个程序。我们还学习了解决此问题的C++程序和完整的方法(普通和高效)。我们可以使用其他语言(如C、Java、Python和其他语言)编写相同的程序。希望您会发现本文有帮助。
以上是使用C++找出在第L个和第R个索引之间只有设置位的数字的详细内容。更多信息请关注PHP中文网其他相关文章!

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

热门话题
 浅析Golang中的的位操作(按位运算符)
Feb 24, 2023 pm 07:42 PM
浅析Golang中的的位操作(按位运算符)
Feb 24, 2023 pm 07:42 PM
在计算机内存昂贵,处理能力有限的美好旧时光里,用比较黑客范的位运算方式去处理信息是首选方式(某些情况下只能如此)。时至今日,直接使用位运算仍然是很多计算领域中不可或缺的部分,例如底层系统编程,图形处理,密码学等。
 使用C++编写代码,找到第N个非平方数
Aug 30, 2023 pm 10:41 PM
使用C++编写代码,找到第N个非平方数
Aug 30, 2023 pm 10:41 PM
我们都知道不是任何数字的平方的数字,如2、3、5、7、8等。非平方数有N个,不可能知道每个数字。因此,在本文中,我们将解释有关无平方数或非平方数的所有内容,以及在C++中查找第N个非平方数的方法。第N个非平方数如果一个数是整数的平方,则该数被称为完全平方数。完全平方数的一些例子是-1issquareof14issquareof29issquareof316issquareof425issquareof5如果一个数不是任何整数的平方,则该数被称为非平方数。例如,前15个非平方数是-2,3,5,6,
 在C编程中,找到一个圆的面积
Aug 25, 2023 pm 10:57 PM
在C编程中,找到一个圆的面积
Aug 25, 2023 pm 10:57 PM
圆是封闭图形。圆上的所有点到圆内一点的距离都相等。中心点称为圆心。点到圆心的距离称为半径。面积是封闭图形尺寸跨度的定量表示。圆的面积是圆的尺寸内包围的面积。计算圆面积的公式,Area=π*r*r为了计算面积,我们给出了圆的半径作为输入,我们将使用公式来计算面积,算法STEP1:Takeradiusasinputfromtheuserusingstdinput.STEP2:Calculatetheareaofcircleusing, area=(
 使用C++编写的数组右旋转的反转算法
Sep 08, 2023 pm 08:17 PM
使用C++编写的数组右旋转的反转算法
Sep 08, 2023 pm 08:17 PM
在本文中,我们将了解逆转算法,将给定的数组向右旋转k个元素,例如−Input:arr[]={4,6,2,6,43,7,3,7},k=4Output:{43,7,3,7,4,6,2,6}Explanation:Rotatingeachelementofarrayby4-elementtotherightgives{43,7,3,7,4,6,2,6}.Input:arr[]={8,5,8,2,1,4,9,3},k=3Output:{4,9,3,8,5,8,2,1}寻找解决方案的方
 使用C++找到数组中唯一配对的数量
Sep 07, 2023 am 11:53 AM
使用C++找到数组中唯一配对的数量
Sep 07, 2023 am 11:53 AM
我们需要适当的知识才能在C++的数组语法中创建几个唯一的对。在查找唯一对的数量时,我们计算给定数组中的所有唯一对,即可以形成所有可能的对,其中每个对应该是唯一的。例如-Input:array[]={5,5,9}Output:4Explanation:Thenumberofalluniquepairsare(5,5),(5,9),(9,5)and(9,9).Input:array[]={5,4,3,2,2}Output:16寻找解决方案的方法有两种方法可以解决这个问题,它们是−
 如何使用Java中的BitSet函数进行位操作
Jun 26, 2023 pm 06:11 PM
如何使用Java中的BitSet函数进行位操作
Jun 26, 2023 pm 06:11 PM
BitSet是Java的一个类,用于进行位操作。可以将BitSet看作一个由二进制位构成的数组,每一个二进制位只能是0或1。BitSet提供了一系列方法来进行位操作,包括设置、清除、翻转、获取等等。在Java中使用BitSet进行位操作很简单,下面我们来介绍一下具体操作步骤。一、创建一个BitSet对象BitSet对象可以通过两种方式来创建:1.使用默认值创
 使用C++编写代码,找到具有相同最小值和最大值的子数组的数量
Aug 25, 2023 pm 11:33 PM
使用C++编写代码,找到具有相同最小值和最大值的子数组的数量
Aug 25, 2023 pm 11:33 PM
在本文中,我们将使用C++解决寻找最大值和最小值相同的子数组数量的问题。以下是该问题的示例−Input:array={2,3,6,6,2,4,4,4}Output:12Explanation:{2},{3},{6},{6},{2},{4},{4},{4},{6,6},{4,4},{4,4}and{4,4,4}arethesubarrayswhichcanbeformedwithmaximumandminimumelementsame.Input:array={3,3,1,5,
 使用C++编写,找到一个集合上的自反关系的数量
Aug 26, 2023 pm 08:17 PM
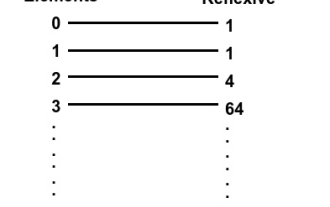
使用C++编写,找到一个集合上的自反关系的数量
Aug 26, 2023 pm 08:17 PM
在本文中,我们将解释在一个集合上找到反身关系的方法。在这个问题中,我们给出一个数字n,以及一个由n个自然数组成的集合,我们必须确定反身关系的数量。反身关系-如果对于集合A中的每个'a',(a,a)属于关系R,则称关系R是集合A上的反身关系。例如-Input:x=1Output:1Explanation:set={1},reflexiverelationsonA*A:{{1}}Input:x=2Output:4Explanation:set={1,2},reflexiverelationsonA*






