C++中的Boruvka算法用于最小生成树

在图论中,寻找连通加权图的最小生成树(MST)是一个常见的问题。MST是图的边的子集,它连接了所有的顶点并最小化了总边权。解决这个问题的一种高效算法是Boruvka算法。
语法
struct Edge {
int src, dest, weight;
};
// Define the structure to represent a subset for union-find
struct Subset {
int parent, rank;
};
算法
现在,让我们概述Boruvka算法中涉及的寻找最小生成树的步骤−
将 MST 初始化为空集。
为每个顶点创建一个子集,其中每个子集只包含一个顶点。
重复以下步骤,直到最小生成树(MST)有V-1条边(V是图中顶点的数量)−
对于每个子集,找到将其连接到另一个子集的最便宜的边。
将选定的边添加到最小生成树中。
对所选边的子集执行并集操作。
输出最小生成树。
方法
在Boruvka算法中,有多种方法可以找到连接每个子集的最便宜的边。以下是两种常见的方法−
方法一:朴素方法
对于每个子集,遍历所有边,并找到将其连接到另一个子集的最小边。
跟踪选定的边并执行联合操作。
示例
#include <iostream>
#include <vector>
#include <algorithm>
struct Edge {
int src, dest, weight;
};
// Define the structure to represent a subset for union-find
struct Subset {
int parent, rank;
};
// Function to find the subset of an element using path compression
int find(Subset subsets[], int i) {
if (subsets[i].parent != i)
subsets[i].parent = find(subsets, subsets[i].parent);
return subsets[i].parent;
}
// Function to perform union of two subsets using union by rank
void unionSets(Subset subsets[], int x, int y) {
int xroot = find(subsets, x);
int yroot = find(subsets, y);
if (subsets[xroot].rank < subsets[yroot].rank)
subsets[xroot].parent = yroot;
else if (subsets[xroot].rank > subsets[yroot].rank)
subsets[yroot].parent = xroot;
else {
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
// Function to find the minimum spanning tree using Boruvka's algorithm
void boruvkaMST(std::vector<Edge>& edges, int V) {
std::vector<Edge> selectedEdges; // Stores the edges of the MST
Subset* subsets = new Subset[V];
int* cheapest = new int[V];
// Initialize subsets and cheapest arrays
for (int v = 0; v < V; v++) {
subsets[v].parent = v;
subsets[v].rank = 0;
cheapest[v] = -1;
}
int numTrees = V;
int MSTWeight = 0;
// Keep combining components until all components are in one tree
while (numTrees > 1) {
for (int i = 0; i < edges.size(); i++) {
int set1 = find(subsets, edges[i].src);
int set2 = find(subsets, edges[i].dest);
if (set1 != set2) {
if (cheapest[set1] == -1 || edges[cheapest[set1]].weight > edges[i].weight)
cheapest[set1] = i;
if (cheapest[set2] == -1 || edges[cheapest[set2]].weight > edges[i].weight)
cheapest[set2] = i;
}
}
for (int v = 0; v < V; v++) {
if (cheapest[v] != -1) {
int set1 = find(subsets, edges[cheapest[v]].src);
int set2 = find(subsets, edges[cheapest[v]].dest);
if (set1 != set2) {
selectedEdges.push_back(edges[cheapest[v]]);
MSTWeight += edges[cheapest[v]].weight;
unionSets(subsets, set1, set2);
numTrees--;
}
cheapest[v] = -1;
}
}
}
// Output the MST weight and edges
std::cout << "Minimum Spanning Tree Weight: " << MSTWeight << std::endl;
std::cout << "Selected Edges:" << std::endl;
for (const auto& edge : selectedEdges) {
std::cout << edge.src << " -- " << edge.dest << " \tWeight: " << edge.weight << std::endl;
}
delete[] subsets;
delete[] cheapest;
}
int main() {
// Pre-defined input for testing purposes
int V = 6;
int E = 9;
std::vector<Edge> edges = {
{0, 1, 4},
{0, 2, 3},
{1, 2, 1},
{1, 3, 2},
{1, 4, 3},
{2, 3, 4},
{3, 4, 2},
{4, 5, 1},
{2, 5, 5}
};
boruvkaMST(edges, V);
return 0;
}
输出
Minimum Spanning Tree Weight: 9 Selected Edges: 0 -- 2 Weight: 3 1 -- 2 Weight: 1 1 -- 3 Weight: 2 4 -- 5 Weight: 1 3 -- 4 Weight: 2
Explanation
的中文翻译为:解释
我们首先定义两个结构 - Edge 和 Subset。 Edge 表示图中的一条边,包含边的源、目的地和权重。 Subset表示并查数据结构的子集,包含父级和排名信息。
find函数是一个辅助函数,它使用路径压缩来查找元素的子集。它递归地查找元素所属的子集的代表(父节点),并压缩路径以优化未来的查询。
unionSets函数是另一个辅助函数,使用按秩合并的方式对两个子集进行合并。它找到两个子集的代表,并根据秩进行合并,以保持平衡树。
boruvkaMST 函数采用边向量和顶点数 (V) 作为输入。它实现了 Boruvka 算法来查找 MST。
在 boruvkaMST 函数内,我们创建一个向量 selectedEdges 来存储 MST 的边。
我们创建一个Subset结构的数组来表示子集,并用默认值初始化它们。
我们还创建了一个数组 cheapest 来跟踪每个子集的最便宜的边。
变量 numTrees 被初始化为顶点的数量,MSTWeight 被初始化为 0。
该算法通过重复组合组件来进行,直到所有组件都在一棵树中。主循环运行直到 numTrees 变为 1。
在主循环的每次迭代中,我们迭代所有边并找到每个子集的最小加权边。如果边连接两个不同的子集,我们用最小加权边的索引更新最便宜的数组。
接下来,我们遍历所有的子集,如果一个子集存在最小权重的边,我们将其添加到selectedEdges向量中,更新MSTWeight,执行子集的并集操作,并减少numTrees的值。
最后,我们输出 MST 权重和选定的边。
主要功能提示用户输入顶点数和边数。然后,它获取每条边的输入(源、目标、权重)并使用输入调用 boruvkaMST 函数。
方法二:使用优先队列
创建一个按照权重排序的优先队列来存储边。
对于每个子集,从优先级队列中找到将其连接到另一个子集的最小权重边。
跟踪选定的边并执行联合操作。
示例
#include <iostream>
#include <vector>
#include <queue>
#include <climits>
using namespace std;
// Edge structure representing a weighted edge in the graph
struct Edge {
int destination;
int weight;
Edge(int dest, int w) : destination(dest), weight(w) {}
};
// Function to find the shortest path using Dijkstra's algorithm
vector<int> dijkstra(const vector<vector<Edge>>& graph, int source) {
int numVertices = graph.size();
vector<int> dist(numVertices, INT_MAX);
vector<bool> visited(numVertices, false);
dist[source] = 0;
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
pq.push(make_pair(0, source));
while (!pq.empty()) {
int u = pq.top().second;
pq.pop();
if (visited[u]) {
continue;
}
visited[u] = true;
for (const Edge& edge : graph[u]) {
int v = edge.destination;
int weight = edge.weight;
if (dist[u] + weight < dist[v]) {
dist[v] = dist[u] + weight;
pq.push(make_pair(dist[v], v));
}
}
}
return dist;
}
int main() {
int numVertices = 4;
vector<vector<Edge>> graph(numVertices);
// Adding edges to the graph
graph[0].push_back(Edge(1, 2));
graph[0].push_back(Edge(2, 5));
graph[1].push_back(Edge(2, 1));
graph[1].push_back(Edge(3, 7));
graph[2].push_back(Edge(3, 3));
int source = 0;
vector<int> shortestDistances = dijkstra(graph, source);
cout << "Shortest distances from source vertex " << source << ":\n";
for (int i = 0; i < numVertices; i++) {
cout << "Vertex " << i << ": " << shortestDistances[i] << endl;
}
return 0;
}
输出
Shortest distances from source vertex 0: Vertex 0: 0 Vertex 1: 2 Vertex 2: 3 Vertex 3: 6
Explanation
的中文翻译为:解释
在这种方法中,我们使用优先队列来优化查找每个子集的最小加权边的过程。下面是代码的详细解释 −
代码结构和辅助函数(如find和unionSets)与之前的方法保持相同。
boruvkaMST 函数被修改为使用优先级队列来有效地找到每个子集的最小加权边。
而不是使用最便宜的数组,我们现在创建一个边的优先队列(pq)。我们用图的边来初始化它。
主循环运行直到 numTrees 变为 1,与之前的方法类似。
在每次迭代中,我们从优先队列中提取最小权重的边(minEdge)。
然后我们使用find函数找到minEdge的源和目标所属的子集。
如果子集不同,我们将minEdge添加到selectedEdges向量中,更新MSTWeight,执行子集的合并,并减少numTrees。
该过程将继续,直到所有组件都在一棵树中。
最后,我们输出 MST 权重和选定的边。
主要功能与之前的方法相同,我们有预定义的输入用于测试目的。
结论
Boruvka 算法为查找加权图的最小生成树提供了一种有效的解决方案。在用 C++ 实现该算法时,我们的团队深入探索了两种不同的路径:一种是传统的或“朴素”的方法。另一个利用优先级队列。取决于当前给定问题的具体要求。每种方法都有一定的优点,可以相应地实施。通过理解和实现 Boruvka 算法,您可以有效地解决 C++ 项目中的最小生成树问题。
以上是C++中的Boruvka算法用于最小生成树的详细内容。更多信息请关注PHP中文网其他相关文章!

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

热门话题
 C语言中的常量是什么,可以举一个例子吗?
Aug 28, 2023 pm 10:45 PM
C语言中的常量是什么,可以举一个例子吗?
Aug 28, 2023 pm 10:45 PM
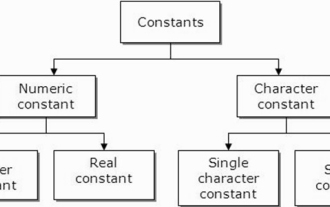
常量也称为变量,一旦定义,其值在程序执行期间就不会改变。因此,我们可以将变量声明为引用固定值的常量。它也被称为文字。必须使用Const关键字来定义常量。语法C编程语言中使用的常量语法如下-consttypeVariableName;(or)consttype*VariableName;不同类型的常量在C编程语言中使用的不同类型的常量如下所示:整数常量-例如:1,0,34,4567浮点数常量-例如:0.0,156.89,23.456八进制和十六进制常量-例如:十六进制:0x2a,0xaa..八进制
 VSCode和VS C++IntelliSense无法工作或拾取库
Feb 29, 2024 pm 01:28 PM
VSCode和VS C++IntelliSense无法工作或拾取库
Feb 29, 2024 pm 01:28 PM
VS代码和VisualStudioC++IntelliSense可能无法拾取库,尤其是在处理大型项目时。当我们将鼠标悬停在#Include<;wx/wx.h>;上时,我们看到了错误消息“CannotOpen源文件‘string.h’”(依赖于“wx/wx.h”),有时,自动完成功能无法响应。在这篇文章中,我们将看到如果VSCode和VSC++IntelliSense不能工作或不能提取库,你可以做些什么。为什么我的智能感知不能在C++中工作?处理大文件时,IntelliSense有时
 如何使用C++中的Prim算法
Sep 20, 2023 pm 12:31 PM
如何使用C++中的Prim算法
Sep 20, 2023 pm 12:31 PM
标题:C++中Prim算法的使用及代码示例引言:Prim算法是一种常用的最小生成树算法,主要用于解决图论中的最小生成树问题。在C++中,通过合理的数据结构和算法实现,可以有效地使用Prim算法。本文将介绍如何在C++中使用Prim算法,并提供具体的代码示例。一、Prim算法简介Prim算法是一种贪心算法,它从一个顶点开始,逐步扩展最小生成树的顶点集合,直到包
 修复Xbox错误代码8C230002
Feb 27, 2024 pm 03:55 PM
修复Xbox错误代码8C230002
Feb 27, 2024 pm 03:55 PM
您是否由于错误代码8C230002而无法在Xbox上购买或观看内容?一些用户在尝试购买或在其控制台上观看内容时不断收到此错误。抱歉,Xbox服务出现问题。稍后再试.有关此问题的帮助,请访问www.xbox.com/errorhelp。状态代码:8C230002这种错误代码通常是由于暂时的服务器或网络问题引起的。但是,还有可能是由于帐户的隐私设置或家长控制等其他原因,这些可能会阻止您购买或观看特定内容。修复Xbox错误代码8C230002如果您尝试在Xbox控制台上观看或购买内容时收到错误代码8C
 递归程序在C++中找到数组的最小和最大元素
Aug 31, 2023 pm 07:37 PM
递归程序在C++中找到数组的最小和最大元素
Aug 31, 2023 pm 07:37 PM
我们以整数数组Arr[]作为输入。目标是使用递归方法在数组中找到最大和最小的元素。由于我们使用递归,我们将遍历整个数组,直到达到长度=1,然后返回A[0],这形成了基本情况。否则,将当前元素与当前最小或最大值进行比较,并通过递归更新其值以供后续元素使用。让我们看看这个的各种输入输出场景−输入 −Arr={12,67,99,76,32};输出 −数组中的最大值:99解释 &mi
 中国东方航空宣布C919客机即将投入实际运营
May 28, 2023 pm 11:43 PM
中国东方航空宣布C919客机即将投入实际运营
May 28, 2023 pm 11:43 PM
5月25日消息,中国东方航空在业绩说明会上披露了关于C919客机的最新进展。据公司表示,与中国商飞签署的C919采购协议已于2021年3月正式生效,其中首架C919飞机已在2022年底交付。预计不久之后,该飞机将正式投入实际运营。东方航空将以上海为主要基地进行C919的商业运营,并计划在2022年和2023年引进总共5架C919客机。公司表示,未来的引进计划将根据实际运营情况和航线网络规划来确定。据小编了解,C919是中国具有完全自主知识产权的全球新一代单通道干线客机,符合国际通行的适航标准。该
 C++程序打印数字的螺旋图案
Sep 05, 2023 pm 06:25 PM
C++程序打印数字的螺旋图案
Sep 05, 2023 pm 06:25 PM
以不同格式显示数字是学习基本编码问题之一。不同的编码概念,如条件语句和循环语句。有不同的程序中,我们使用特殊字符(如星号)来打印三角形或正方形。在本文中,我们将以螺旋形式打印数字,就像C++中的正方形一样。我们将行数n作为输入,然后从左上角开始移向右侧,然后向下,然后向左,然后向上,然后再次向右,以此类推等等。螺旋图案与数字123456724252627282982340414243309223948494431102138474645321120373635343312191817161514
 C语言中的void关键字的作用
Feb 19, 2024 pm 11:33 PM
C语言中的void关键字的作用
Feb 19, 2024 pm 11:33 PM
C中的void是一个特殊的关键字,用来表示空类型,也就是指没有具体类型的数据。在C语言中,void通常用于以下三个方面。函数返回类型为void在C语言中,函数可以有不同的返回类型,例如int、float、char等。然而,如果函数不返回任何值,则可以将返回类型设为void。这意味着函数执行完毕后,并不返回具体的数值。例如:voidhelloWorld()






