树中所有对最短路径之和

在树中,“所有节点对最短路径之和”的术语指的是计算所有节点对的个别最短路径的总和。一种有效的方法是使用双重DFS(深度优先搜索)算法。在第一次DFS遍历期间确定所选节点与每个其他节点之间的距离。在第二次DFS遍历期间再次遍历树,将每个节点视为潜在的LCA(最低公共祖先),并计算所选LCA的后代节点对之间的距离之和。使用这种方法可以计算出树中所有节点对最短路径之和,并确保得到一个理想的解决方案
使用的方法
双重 DFS(深度优先搜索)方法
动态规划方法
双重 DFS(深度优先搜索)方法
对于树中所有对最短路径的总和,我们使用双重 DFS(深度优先搜索)方法,该方法涉及两次 DFS 遍历。首先,我们计算从任何节点开始到所有其他节点的距离。然后,在第二次 DFS 遍历期间,我们导航树,同时将每个节点视为潜在的 LCA。我们在遍历时计算并求和作为所选 LCA 后代的节点对之间的距离。通过对所有节点重复此过程,我们获得所有对最短路径的总和。该策略对于这个问题非常引人注目,因为它有效地计算了树中所有节点集之间的距离总和。
算法
树中的任何节点都可以作为起始节点
为了确定从选择的起始节点到所有其他节点的距离,从该节点开始执行深度优先搜索(DFS)。这些距离应该保存在一个数组或数据结构中。
接下来,在树上运行第二次深度优先搜索(DFS),将每个节点视为可能的最近公共祖先(LCA)
在第二次 DFS 期间遍历树时,计算作为所选 LCA 后代的节点对之间的距离。对于每个 LCA,将这些距离加在一起。
对树中的每个节点重复此过程
树中最有限方式的所有匹配的总和由步骤 4 中所有计算距离的总和表示。
Example
的中文翻译为:示例
#include <iostream>
#include <vector>
using namespace std;
const int MAXN = 10005;
vector<int> graph[MAXN];
int ancestor[MAXN];
int dfs(int node, int lca, int distance) {
int sum = 0;
for (int neighbor : graph[node]) {
if (neighbor != lca) {
sum += dfs(neighbor, lca, distance + 1);
}
}
return sum + distance;
}
int main() {
int lca_node = 0;
int total_sum = 0;
for (int node = 0; node < MAXN; ++node) {
if (node != lca_node) {
total_sum += dfs(node, lca_node, 0);
}
}
cout << "Total sum of distances between descendants of the LCA: " << total_sum << endl;
return 0;
}
输出
Total sum of distances between descendants of the LCA: 0
动态规划方法:
我们首先选择任意一个节点作为根节点,并在动态规划方法中将树转化为有根树,用于计算树中所有节点间最短路径之和。我们利用动态规划计算每个节点与根节点之间的分割,并将结果存储在一个数组中。然后,对于每个节点,我们将其子节点与根节点的分离(已计算)相加,以确定所有其他节点的整体分离。通过这种方式,我们能够快速计算出所有节点间最短路径的总数。作为解决该问题的有效方法,该算法的时间复杂度为O(N),其中N是树中节点的数量。
算法
将树中的任何节点作为根并以树为根(例如,使用根节点的深度搜索)以创建有根树。
动态规划可用于确定每个节点距根的距离。这些距离应该存储在数组或数据结构中。
计算树中每个节点到所有其他节点的距离的总和:
树中所有对最短路径的总和就是最终结果。
a.遍历当前节点的子节点。
b.要考虑通过当前节点的路径,请将每个子树的子树中的节点数以及之前为每个子树计算的到根的距离相加。
c. 对于活动节点的每个子节点,将这些金额相加
d.将当前节点的总计添加到最终结果中。
#include <iostream>
#include <vector>
using namespace std;
struct TreeNode {
int val;
vector<TreeNode*> children;
};
int dfs(TreeNode* node, vector<int>& distances) {
int subtree_size = 1;
for (TreeNode* child : node->children) {
subtree_size += dfs(child, distances);
distances[node->val] += distances[child->val] + subtree_size;
}
return subtree_size;
}
int sumOfAllPairShortestPaths(TreeNode* root) {
vector<int> distances(root->val + 1, 0);
dfs(root, distances);
int total_sum = 0;
for (int distance : distances) {
total_sum += distance;
}
return total_sum;
}
int main() {
TreeNode* root = new TreeNode{0};
int result = sumOfAllPairShortestPaths(root);
cout << "Sum of all pair shortest paths in the tree: " << result << endl;
return 0;
}
输出
Sum of all pair shortest paths in the tree: 0
结论
树中所有对最短路径的总和可以使用 Double DFS(深度优先搜索)方法或动态规划来计算。 Double DFS 方法由两遍组成,首先计算从选定节点到所有其他节点的距离,然后再次遍历树,同时将每个节点视为潜在的最低公共祖先 (LCA),以将之间的距离相加后代节点对。动态规划方法需要递归地使用 DFS 来建立树的根并计算从根到每个其他节点的距离。两种方法的结果是相同的,并且由树中所有成对最短路径的总和组成。两种算法之间的决策可能基于特定的实现偏好或树结构,但两种算法都提供了有效的解决方案。
以上是树中所有对最短路径之和的详细内容。更多信息请关注PHP中文网其他相关文章!

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

热门话题
 树中所有对最短路径之和
Aug 28, 2023 pm 03:17 PM
树中所有对最短路径之和
Aug 28, 2023 pm 03:17 PM
在树中,“所有节点对最短路径之和”的术语指的是计算所有节点对的个别最短路径的总和。一种有效的方法是使用双重DFS(深度优先搜索)算法。在第一次DFS遍历期间确定所选节点与每个其他节点之间的距离。在第二次DFS遍历期间再次遍历树,将每个节点视为潜在的LCA(最低公共祖先),并计算所选LCA的后代节点对之间的距离之和。使用这种方法可以计算出树中所有节点对最短路径之和,并确保得到一个理想的解决方案使用的方法双重DFS(深度优先搜索)方法动态规划方法双重DFS(深度优先搜索)方法对于树中所有对最短路径的
 如何使用java实现最短路径算法
Sep 19, 2023 am 08:18 AM
如何使用java实现最短路径算法
Sep 19, 2023 am 08:18 AM
如何使用Java实现最短路径算法概述:最短路径算法是图论中一个重要的应用,在网络路由、地图导航等领域都有广泛的应用。在这篇文章中,我们将学习如何使用Java实现最短路径算法,并提供具体的代码示例。算法思路:最短路径算法有多种实现方式,其中最著名的两种算法是Dijkstra算法和A*算法。在这里我们将重点介绍Dijkstra算法的实现。Dijkstra算法的基
 深入探索Java中树和图的非线性数据结构应用和实现方法
Dec 26, 2023 am 10:22 AM
深入探索Java中树和图的非线性数据结构应用和实现方法
Dec 26, 2023 am 10:22 AM
理解Java中的树和图:探索非线性数据结构的应用与实现引言在计算机科学中,数据结构是计算机中存储、组织和管理数据的方式。数据结构可以分为线性数据结构和非线性数据结构。树和图是非线性数据结构中最常用的两种类型。本文将重点介绍Java中树和图的概念、应用和实现,并给出具体的代码示例。树的概念与应用树是一种抽象数据类型,由节点和边组成的集合。树的每个节点包含一个数
 递归在 C++ 数据结构中的妙用:栈和树的实现
May 04, 2024 pm 01:54 PM
递归在 C++ 数据结构中的妙用:栈和树的实现
May 04, 2024 pm 01:54 PM
递归在C++数据结构中的应用:栈:通过后进先出(LIFO)结构递归实现栈。树:通过分层结构递归实现树,支持插入和深度计算等操作。递归为处理嵌套结构提供了简洁高效的解决方案,使数据结构的实现更加直观和易于维护。
 使用弗洛伊德-沃沙尔算法找到任意两个节点之间的最短路径
Sep 20, 2023 pm 02:21 PM
使用弗洛伊德-沃沙尔算法找到任意两个节点之间的最短路径
Sep 20, 2023 pm 02:21 PM
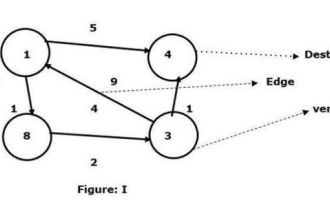
C++有一个宏,它被定义为一段代码或期望的值,并且每当用户需要时,它将被重复使用。弗洛伊德-沃尔夏尔算法是在给定的加权图中找到所有顶点对之间最短路径的过程。该算法遵循动态规划的方法来找到最小权重图。让我们通过图表来理解弗洛伊德-沃尔夏尔算法的含义-以顶点1为源,顶点4为目的地,求它们之间的最短路径。我们已经看到有两条路径可以连接到目标顶点4。1->4–边的权重为51->8->3->4–边权重(1+2+1)为4。在给定的图I中,我们看到两个顶点之间连接的最小边。所以这里顶点
 PHP算法设计思路:如何实现图的最短路径问题的高效解决方案?
Sep 19, 2023 pm 03:43 PM
PHP算法设计思路:如何实现图的最短路径问题的高效解决方案?
Sep 19, 2023 pm 03:43 PM
PHP算法设计思路:如何实现图的最短路径问题的高效解决方案?在实际开发中,我们经常需要解决最短路径问题,例如在地图导航、网络路由、物流配送等领域。而图的最短路径算法是解决这类问题的关键。图由一组顶点和一组边组成。顶点表示节点,边表示节点之间的关系。最短路径问题就是找到连接两个节点的最短路径。在PHP中,我们可以使用多种算法来解决最短路径问题,其中最著名的算法
 使用C++实现删除所有不在任何路径上且路径和小于k的节点
Sep 04, 2023 am 10:17 AM
使用C++实现删除所有不在任何路径上且路径和小于k的节点
Sep 04, 2023 am 10:17 AM
在这个问题中,我们有一个二叉树,其从根节点到叶节点的路径是完全定义的。从根节点到叶子节点的所有节点之和必须大于或等于k。所以我们需要删除路径中总和小于k的所有节点。这里要记住的重要一点是,一个节点可能是许多路径的一部分,因此只有当所有路径的总和left的总和为10+20+5,即25,小于150,我们需要对其进行修剪并删除5。之后,让我们评估10->30->40。它小于150,所以删除40。现在我们看到另一条路径10->20->35->50,总和115小于150,所以
 C++程序以移除不满足路径和大于等于k的节点
Sep 14, 2023 am 11:25 AM
C++程序以移除不满足路径和大于等于k的节点
Sep 14, 2023 am 11:25 AM
在这个问题中,我们有一个二叉树,其从根节点到叶节点的路径是完全定义的。从根节点到叶节点的所有节点的总和必须大于或等于常数值k。因此,我们需要删除那些总和小于k的路径中的所有节点,这样树中剩下的路径将大于k。这里要记住的重要一点是,一个节点可能是许多路径的一部分,因此只有当通向该节点的所有路径的总和left的总和为10+20+5,即25,小于150,我们需要对其进行修剪并删除5。之后,让我们评估10->30->40。它小于150,因此删除40。现在我们看到另一条路径10->20-






