一个内接于另一个几何形状或立体的平面形状或立体是被封闭并且“紧密适应”于其内部的。说“正方形内接于三角形”与“三角形外接于正方形”是完全相同的意思。
能够内接于等边三角形的最大正方形−
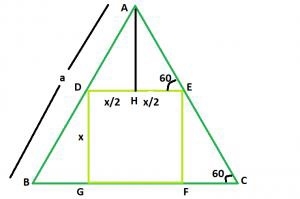
能够内接于等边三角形的最大正方形−
让我们举个例子,
Input: 5 Output: 2.32
正方形的一边为x。
现在,AH与DE垂直。
DE平行于BC,角AED = angle ACB = 60
在三角形EFC中,
⇒ Sin60 = x/ EC
⇒ √3 / 2 = x/EC
⇒ EC = 2x/√3
在三角形AHE中,
⇒ Cos 60 = x/2AE
⇒ 1/2 = x/2AE
⇒ AE = x
三角形的边AC = 2x/√3 + x。现在,
a = 2x/√3 + x
x = a/(1 + 2/√3) = 0.464a
演示
#include <stdio.h>
#include <math.h>
int main() {
float a = 5;
float area = 0.464 * a;
printf("The area is : %f",area);
return 0;
}The area is : 2.320000
以上是在一个等边三角形内切的最大正方形是多大?的详细内容。更多信息请关注PHP中文网其他相关文章!




