使用C++找到遍历N叉树的方式的数量
给定一个N叉树,我们的任务是找到遍历这棵树的总方式数,例如 −
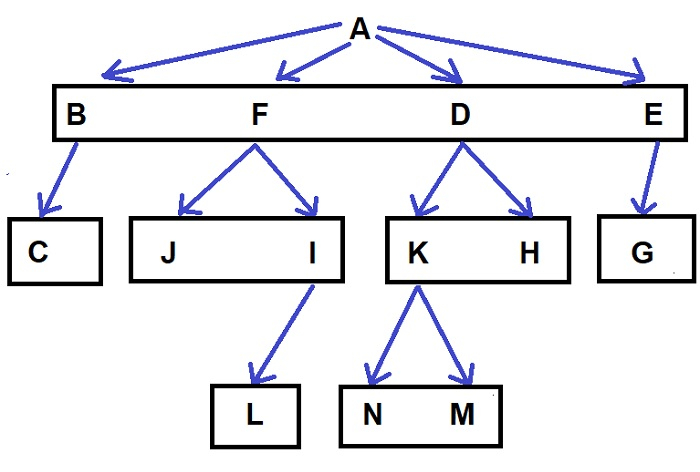
对于上面的树,我们的输出将是192。
对于这个问题,我们需要一些组合学的知识。现在在这个问题中,我们只需要检查每条路径的所有可能组合,这将给我们答案。
找到解决方案的方法
在这个方法中,我们只需要执行一次层次遍历,检查每个节点有多少个子节点,然后将其阶乘乘以答案。
示例
上述方法的C++代码
#include<bits/stdc++.h>
using namespace std;
struct Node{ // structure of our node
char key;
vector<Node *> child;
};
Node *createNode(int key){ // function to initialize a new node
Node *temp = new Node;
temp->key = key;
return temp;
}
long long fact(int n){
if(n <= 1)
return 1;
return n * fact(n-1);
}
int main(){
Node *root = createNode('A');
(root->child).push_back(createNode('B'));
(root->child).push_back(createNode('F'));
(root->child).push_back(createNode('D'));
(root->child).push_back(createNode('E'));
(root->child[2]->child).push_back(createNode('K'));
(root->child[1]->child).push_back(createNode('J'));
(root->child[3]->child).push_back(createNode('G'));
(root->child[0]->child).push_back(createNode('C'));
(root->child[2]->child).push_back(createNode('H'));
(root->child[1]->child).push_back(createNode('I'));
(root->child[2]->child[0]->child).push_back(createNode('N'));
(root->child[2]->child[0]->child).push_back(createNode('M'));
(root->child[1]->child[1]->child).push_back(createNode('L'));
queue<Node*> q;
q.push(root);
long long ans = 1;
while(!q.empty()){
auto z = q.front();
q.pop();
ans *= fact(z -> child.size());
cout << z->child.size() << " ";
for(auto x : z -> child)
q.push(x);
}
cout << ans << "\n";
return 0;
}Output
4 1 2 2 1 0 0 1 2 0 0 0 0 0 192
上述代码的解释
在这种方法中,我们应用BFS(广度优先搜索)或层次遍历,并检查每个节点的子节点数量。然后,将该数量的阶乘乘以我们的答案。
结论
本教程介绍了几种遍历N叉树组合的方法,并应用了BFS。我们还学习了解决这个问题的C++程序和完整的方法。
我们可以用其他语言(如C、Java、Python和其他语言)编写相同的程序。希望你觉得这个教程有帮助。
以上是使用C++找到遍历N叉树的方式的数量的详细内容。更多信息请关注PHP中文网其他相关文章!

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

热门话题
 OpenOOD更新v1.5:全面、精确的分布外检测代码库及测试平台,支持在线排行榜、一键测试
Jul 03, 2023 pm 04:41 PM
OpenOOD更新v1.5:全面、精确的分布外检测代码库及测试平台,支持在线排行榜、一键测试
Jul 03, 2023 pm 04:41 PM
分布外(OOD)检测对于开放世界智能系统的可靠运行至关重要,但目前面向对象的检测方法存在「评估不一致」(evaluationinconsistencies)的问题。之前的工作OpenOODv1统一了OOD检测的评估,但在可扩展性和可用性方面仍然存在限制。最近开发团队再次提出OpenOODv1.5,相比上一版本,新的OOD检测方法评估在确保准确、标准化和用户友好等方面得到显著提升。图片Paper:https://arxiv.org/abs/2306.09301OpenOODCodebase:htt
 涨知识!用逻辑规则进行机器学习
Apr 01, 2023 pm 10:07 PM
涨知识!用逻辑规则进行机器学习
Apr 01, 2023 pm 10:07 PM
在准确率-召回率曲线上,同样的点是用不同的坐标轴绘制的。警告:左边的第一个红点(0%召回率,100%精度)对应于0条规则。左边的第二个点是第一个规则,等等。 Skope-rules使用树模型生成规则候选项。首先建立一些决策树,并将从根节点到内部节点或叶子节点的路径视为规则候选项。然后通过一些预定义的标准(如精确度和召回率)对这些候选规则进行过滤。只有那些精确度和召回率高于其阈值的才会被保留。最后,应用相似性过滤来选择具有足够多样性的规则。一般情况下,应用Skope-rules来学习每个根本原因的
 如何在Java中找到运行时提供的参数数量?
Sep 23, 2023 pm 01:13 PM
如何在Java中找到运行时提供的参数数量?
Sep 23, 2023 pm 01:13 PM
在Java中,在运行时传递参数的一种方法是使用命令行或终端。在检索命令行参数的这些值时,我们可能需要查找用户在运行时提供的参数数量,这可以借助length属性来实现。本文旨在借助示例程序解释传递和获取用户提供的参数数量的过程。获取用户在运行时提供的参数数量在查找命令行参数的数量之前,我们的第一步是创建一个允许用户在运行时传递参数的程序。字符串[]参数在编写Java程序时,我们经常遇到main()方法。当JVM调用此方法时,Java应用程序开始执行。它与一个名为String[]args的参数一起使
 Linux命令:查看telnet进程数量的方法
Mar 01, 2024 am 11:39 AM
Linux命令:查看telnet进程数量的方法
Mar 01, 2024 am 11:39 AM
Linux命令是系统管理员日常工作中必不可少的工具之一,它们可以帮助我们完成各种系统管理任务。在运维工作中,有时候需要查看系统中某个进程的数量以便及时发现问题和进行调优。本文将介绍如何使用Linux命令查看telnet进程的数量,让我们一起来学习吧。在Linux系统中,我们可以使用ps命令结合grep命令来查看telnet进程的数量。首先,我们需要打开终端,
 使用C++编写代码,找到具有相同最小值和最大值的子数组的数量
Aug 25, 2023 pm 11:33 PM
使用C++编写代码,找到具有相同最小值和最大值的子数组的数量
Aug 25, 2023 pm 11:33 PM
在本文中,我们将使用C++解决寻找最大值和最小值相同的子数组数量的问题。以下是该问题的示例−Input:array={2,3,6,6,2,4,4,4}Output:12Explanation:{2},{3},{6},{6},{2},{4},{4},{4},{6,6},{4,4},{4,4}and{4,4,4}arethesubarrayswhichcanbeformedwithmaximumandminimumelementsame.Input:array={3,3,1,5,
 使用C++找到遍历N叉树的方式的数量
Sep 04, 2023 pm 05:01 PM
使用C++找到遍历N叉树的方式的数量
Sep 04, 2023 pm 05:01 PM
给定一个N叉树,我们的任务是找到遍历这棵树的总方式数,例如−对于上面的树,我们的输出将是192。对于这个问题,我们需要一些组合学的知识。现在在这个问题中,我们只需要检查每条路径的所有可能组合,这将给我们答案。找到解决方案的方法在这个方法中,我们只需要执行一次层次遍历,检查每个节点有多少个子节点,然后将其阶乘乘以答案。示例上述方法的C++代码#include<bits/stdc++.h>usingnamespacestd;structNode{//s
 二叉树中等腰三角形的数量
Sep 05, 2023 am 09:41 AM
二叉树中等腰三角形的数量
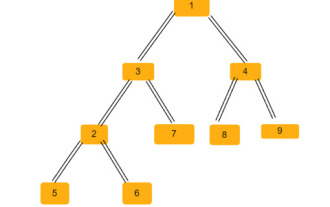
Sep 05, 2023 am 09:41 AM
二叉树是一种数据结构,其中每个节点最多可以有两个子节点。这些孩子分别称为左孩子和右孩子。假设我们得到了一个父数组表示,您必须使用它来创建一棵二叉树。二叉树可能有几个等腰三角形。我们必须找到该二叉树中可能的等腰三角形的总数。在本文中,我们将探讨几种在C++中解决这个问题的技术。理解问题给你一个父数组。您必须以二叉树的形式表示它,以便数组索引形成树节点的值,而数组中的值给出该特定索引的父节点。请注意,-1始终是根父节点。下面给出的是一个数组及其二叉树表示。Parentarray=[0,-1,3,1,
 使用C++编写代码,找到具有奇数和的子数组的数量
Sep 21, 2023 am 08:45 AM
使用C++编写代码,找到具有奇数和的子数组的数量
Sep 21, 2023 am 08:45 AM
子数组是数组的连续部分。例如,我们考虑一个数组[5,6,7,8],那么有十个非空子数组,如(5),(6),(7),(8),(5,6),(6,7)、(7,8)、(5,6,7)、(6,7,8)和(5,6,7,8)。在本指南中,我们将解释在C++中查找所有可能的信息来查找具有奇数和的子数组的数量。为了找到奇数和的子数组的数量,我们可以使用不同的方法,所以这里是一个简单的例子-Input:array={9,8,7,6,5}Output:9Explanation:Sumofsubarray-{9}=9{7






