在C程序中使用递归函数的辅助空间?

这里我们将看到递归函数调用如何需要辅助空间。它与普通函数调用有何不同?
假设我们有一个如下所示的函数 -
long fact(int n){
if(n == 0 || n == 1)
return 1;
return n * fact(n-1);
}该函数是递归函数。当我们像fact(5)一样调用它时,它将在堆栈内存储地址,如下所示 -
fact(5) ---> fact(4) ---> fact(3) ---> fact(2) ---> fact(1)
随着递归函数一次又一次地调用自身,地址被添加到堆栈中。因此,如果函数被递归调用 n 次,它将占用 O(n) 辅助空间。但这并不意味着如果一个普通函数被调用 n 次,空间复杂度将为 O(n)。对于普通函数,调用时会将地址压入堆栈。完成后,将从堆栈中弹出地址并进入调用者函数。然后再打电话。所以它的复杂度为 O(1)。
以上是在C程序中使用递归函数的辅助空间?的详细内容。更多信息请关注PHP中文网其他相关文章!

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

热门话题
 将以下内容翻译为中文:C程序将罗马数字转换为十进制数字
Sep 05, 2023 pm 09:53 PM
将以下内容翻译为中文:C程序将罗马数字转换为十进制数字
Sep 05, 2023 pm 09:53 PM
给出以下是一个将罗马数字转换为十进制数字的C语言算法:算法步骤1-开始步骤2-在运行时读取罗马数字步骤3-长度:=strlen(roman)步骤4-对于i=0到长度-1 步骤4.1-switch(roman[i]) 步骤4.1.1-case'm': &nbs
 C++ 递归函数的优化技巧有哪些?
Apr 17, 2024 pm 12:24 PM
C++ 递归函数的优化技巧有哪些?
Apr 17, 2024 pm 12:24 PM
为了优化递归函数的性能,可以采用以下技巧:使用尾递归:将递归调用放在函数末尾,避免递归开销。备忘录化:存储已计算的结果,避免重复计算。分治法:分解问题,递归解决子问题,提高效率。
 C++程序以给定值为参数,找到双曲正弦反函数的值
Sep 17, 2023 am 10:49 AM
C++程序以给定值为参数,找到双曲正弦反函数的值
Sep 17, 2023 am 10:49 AM
双曲函数是使用双曲线而不是圆定义的,与普通三角函数相当。它从提供的弧度角返回双曲正弦函数中的比率参数。但要做相反的事,或者换句话说。如果我们想根据双曲正弦值计算角度,我们需要像双曲反正弦运算一样的反双曲三角运算。本课程将演示如何使用C++中的双曲反正弦(asinh)函数,使用双曲正弦值(以弧度为单位)计算角度。双曲反正弦运算遵循以下公式-$$\mathrm{sinh^{-1}x\:=\:In(x\:+\:\sqrt{x^2\:+\:1})},其中\:In\:是\:自然对数\:(log_e\:k)
 C程序以找到链表的长度
Sep 07, 2023 pm 07:33 PM
C程序以找到链表的长度
Sep 07, 2023 pm 07:33 PM
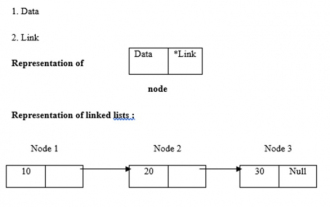
链接列表使用动态内存分配,即它们相应地增长和收缩。它们被定义为节点的集合。这里,节点有两部分,即数据和链路。数据、链接和链表的表示如下-链表的类型链表有四种类型,如下:-单链表/单链表双/双向链表循环单链表循环双链表我们使用递归方法求链表长度的逻辑是-intlength(node*temp){ if(temp==NULL) returnl; else{&n
 C++ 递归函数在搜索算法中的应用?
Apr 17, 2024 pm 04:30 PM
C++ 递归函数在搜索算法中的应用?
Apr 17, 2024 pm 04:30 PM
递归函数在搜索算法中用于探索树状数据结构。深度优先搜索使用堆栈探索节点,而广度优先搜索使用队列按层遍历。在实际应用中,如查找文件中,递归函数可用于在指定目录中搜索给定文件。
 C++程序打印字典
Sep 11, 2023 am 10:33 AM
C++程序打印字典
Sep 11, 2023 am 10:33 AM
映射是C++中的一种特殊类型的容器,其中每个元素都是一对两个值,即键值和映射值。键值用于索引每个项目,映射值是与键关联的值。无论映射值是否唯一,键始终是唯一的。要在C++中打印映射元素,我们必须使用迭代器。一组项目中的一个元素由迭代器对象指示。迭代器主要与数组和其他类型的容器(例如向量)一起使用,并且它们具有一组特定的操作,可用于识别特定范围内的特定元素。可以增加或减少迭代器来引用范围或容器中存在的不同元素。迭代器指向范围内特定元素的内存位置。使用迭代器在C++中打印地图首先,我们看一下如何定义
 C程序使用rename()函数更改文件名
Sep 21, 2023 pm 10:01 PM
C程序使用rename()函数更改文件名
Sep 21, 2023 pm 10:01 PM
rename函数将文件或目录从旧名称更改为新名称。此操作类似于移动操作。因此,我们也可以使用此rename函数来移动文件。此函数存在于stdio.h库头文件中。rename函数的语法如下:intrename(constchar*oldname,constchar*newname);rename()函数的功能它接受两个参数。一个是oldname,另一个是newname。这两个参数都是指向常量字符的指针,用于定义文件的旧名称和新名称。如果文件重命名成功,则返回零;否则,返回非零整数。在重命名操作期间
 C++ 递归函数的退出条件是什么?
Apr 17, 2024 am 11:33 AM
C++ 递归函数的退出条件是什么?
Apr 17, 2024 am 11:33 AM
C++递归函数的退出条件包括:基线条件:检查函数是否达到可直接返回结果的状态,通常判断某个条件或参数值是否满足阈值。递归终止条件:替代或补充基线条件,确保函数在一定数量的递归调用后停止,通过跟踪递归深度或设置最大递归深度限制实现。






