如果平面上没有超过两个点共线，那么三角形的数量是多少？

让我们看看如何在给定 n 个点的平面上计算三角形的数量，并限制共线的点不超过两个。

计算共线点不超过两个的平面中的三角形数量是计算几何中的典型问题，它应用于计算机图形学、图像处理和计算机科学的其他领域。

例如，在从 3D 图形中的 3D 场景创建 2D 图像时，可能会出现计算共线点不超过两个的平面中的三角形的问题。在这种情况下，三角形计数过程可用于确定将 3D 场景投影到平面上后最终 2D 图像中存在多少个三角形。由此可以确定场景的复杂程度，提高渲染速度。

在图像处理中，我们可能想要计算图像中唯一对象或形状的数量，这个问题很有帮助。在这种情况下，我们可以将图像表示为平面上的点的集合，然后我们可以通过应用三角形计数技术来计算这些点之间可以创建的三角形的数量。我们可以通过计算形成的三角形数量来确定图像中不同项目或形状的大致数量。

说明

让我们通过几个例子来理解这个问题并尝试解决它。​​

目的是确定在具有 n 个点的平面上形成多少个三角形，使得不超过两个点共线。

示例 -

假设 N 是平面上的点数。

N = 3

使用这些点我们只能绘制一个三角形。

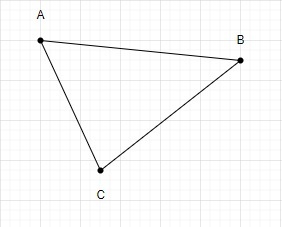
因此，使用 3 个点组成的三角形总数为 1。

让 N = 4

让我们用这四个点绘制三角形。

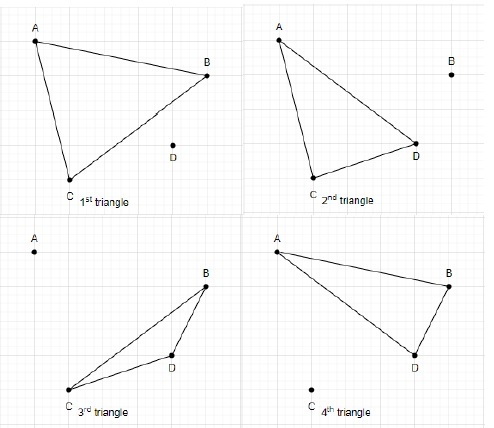
使用 4 个点形成的三角形总数为 4。

让我们看看计算三角形数量所涉及的一些数学知识。这可以使用排列和组合来获得。要构建三角形，一次需要总数中的 3 个点。

因此，如果一个平面包含 n 个点，并且其中不超过两个点共线，则该平面中三角形的数量由以下公式给出。

$$mathrm{n_{C_{3}}:=:frac{n(n-1):(n-2)}{6}}$$

方法

如果不超过两个点共线，则程序查找平面中三角形的数量，使用以下算法。

• 将平面上的点数作为输入，并限制不超过两个共线点。

• 使用上述公式计算三角形的总数。

• 打印三角形总数作为输出。

示例

如果不超过两点共线，则计算平面中三角形的数量的 C++ 程序。

#include <iostream>
using namespace std;

int main() {
   int number_of_points = 4;
   int number_of_triangle;
   
   number_of_triangle = number_of_points * (number_of_points - 1) * (number_of_points - 2) / 6;
   cout << "Total number of triangles formed using " << number_of_points<< " points = " <<  number_of_triangle << endl;
   
   return 0;
}

输出

Total number of triangles formed using 4 points = 4

复杂性

时间复杂度：O(1)，因为无论输入大小如何，此代码都会执行固定数量的计算。

空间复杂度：O(1)，因为代码使用固定数量的变量来存储输入值和结果，而不管输入的大小。

结论

在本文中，我们尝试解释查找具有 n 个给定点的可能三角形总数的方法，约束条件是没有两点共线。我希望这篇文章可以帮助您更好地学习这个概念。

以上是如果平面上没有超过两个点共线，那么三角形的数量是多少？的详细内容。更多信息请关注PHP中文网其他相关文章！