N元树中的同构性
同构被定义为两棵树具有相同或镜像结构。在镜像结构的情况下,左节点的数据将始终与右节点匹配。例如,我们将取一个最接近镜像的数字,看看它的反向是什么,这就是同构的真正概念。
在本文中,我们将检查两个不同的二叉树是否同构。
让我们以N叉树的同构为例-

请注意,L代表左节点,而R代表右节点
左侧最左第二分区的P和Q树的镜像结构

这两个图示展示了它们如何通过给出四个匹配条件(P和Q的根节点)来彼此同构。
左-左节点可以匹配。
要么可以匹配右-右节点。
左右节点均可匹配。
要么右左无法匹配。
语法
程序中使用了以下语法−
struct name_of_structure{
data_type var_name;
// data member or field of the structure.
}
参数
struct − 这个关键字用于表示结构数据类型。
name_of_structure − 我们为结构提供任何名称。
结构是将各种相关变量集中在一个地方的集合。
算法
我们将使用一个名为‘iostream’的头文件来开始程序。
我们正在创建名为‘tree_node’的结构,其中包含整数类型‘d’和初始化指针变量- ‘l’和‘r’,分别表示左右子节点的数据。
现在我们使用一个名为‘create_node()’的函数创建另一个结构,该函数接受一个名为‘data’的参数来指定根节点的值。同时,我们创建一个名为‘tree_node’的指针,并使用给定的数据来初始化左子节点和右子节点的指针为空,并返回根节点。使用这个函数,我们将插入左子节点和右子节点的节点。
我们正在创建一个名为‘check_isomorphism_tree 的函数,它使用布尔数据类型,以两个tree_node指针p和q作为输入参数,并返回一个布尔值。在其中,我们两次创建一个“if语句”来检查p中的数据是否等同于q中的数据。
检查p和q是否都为null,如果是,则返回true,因为树是同构的。
检查 p 或 q 中是否有任何一个为 null,如果是,则返回 false,因为这两棵树不是同构的。
在‘check_isomorphism_tree’函数中,我们使用逻辑运算符“&&”和“||”递归检查节点‘p’和‘q’的所有可能的左右子节点组合。
我们从主函数开始,创建两个树节点“p”和“q”来提供信息。
在主函数中,我们使用if语句调用‘check_isomorphism_tree’函数,并传递给定的参数p和q来验证这些整数值是否同构。如果它们是同构的,则打印语句为“这个给定的节点信息将生成同构树”,否则相反。
Example
的中文翻译为:示例
在这个程序中,我们将检查两个二叉树是否同构。
#include<iostream>
using namespace std;
struct tree_node{
int d;
tree_node*l; // l = left
tree_node*r; // r = right
};
struct tree_node* create_node(int data){
struct tree_node*root= new tree_node;
root->d= data;
root->l= NULL;
root->r= NULL;
return root;
}
bool check_isomorphism_tree(tree_node*p, tree_node*q) {
// p and q both are different tree
if(p==NULL and q==NULL){
return true;
}
if(p==NULL or q==NULL){
return false;
}
// return all the possible condition
return (p->d==q->d && ((check_isomorphism_tree(p->l,q->r)&& check_isomorphism_tree(p->r,q->l))||(check_isomorphism_tree(p->l,q->l)&& check_isomorphism_tree(p->r,q->r))));
}
int main(){
// Tree of root p
struct tree_node *p = create_node(10);
p->l = create_node(5);
p->r = create_node(4);
p->l->l = create_node(11);
p->r->r = create_node(12);
p->l->r = create_node(51);
p->r->l = create_node(6);
p->l->r->l = create_node(7); // left->right->left
p->l->l->l = create_node(9); // left->left->left
// Tree of root q
struct tree_node *q = create_node(10);
q->l = create_node(5);
q->r = create_node(4);
q->l->l = create_node(11);
q->r->r = create_node(12);
q->l->r = create_node(51);
q->r->l = create_node(6);
q->l->r->l = create_node(7);
q->l->l->l = create_node(9);
if(check_isomorphism_tree(p,q)){
cout<<"This given information of node will make isomorphism tree"<<endl;
} else {
cout<<" This given information of node will not make isomorphism tree "<<endl;
}
return 0;
}
输出
This given information of node will make isomorphism tree
结论
在这个程序中,我们理解了N叉树中同构的概念。我们看到了如何使用结构来表示树节点,以及使用左-左节点、右-左节点、左-右-左节点等来构建树,以下操作有助于满足树的同构性质。
以上是N元树中的同构性的详细内容。更多信息请关注PHP中文网其他相关文章!

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

Video Face Swap
使用我们完全免费的人工智能换脸工具轻松在任何视频中换脸!

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)
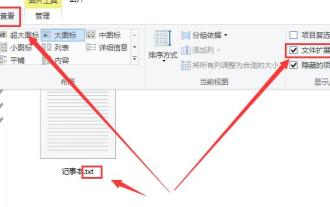 如何修改Win10记事本的文件扩展名
Jan 04, 2024 pm 12:49 PM
如何修改Win10记事本的文件扩展名
Jan 04, 2024 pm 12:49 PM
在使用记事本的时候,我们因为需要处理的事情不同,时长会需要更改记事本的扩展名,那么扩展名需要怎么去更改呢,其实只需要使用重命名功能就能修改扩展名了。win10记事本的扩展名怎么改:1、我们在文件夹中,首先点击上方的,勾选上。2、这样文件的扩展名就能显示出来了,然后右键你的记事本,选择3、选中.后面的进行更改。4、如改成.jpeg格式的。然后会弹出提示,点击。5、更改完成了,就是这样的了。
 如何将HTML转换为MP4格式
Feb 19, 2024 pm 02:48 PM
如何将HTML转换为MP4格式
Feb 19, 2024 pm 02:48 PM
标题:HTML如何转换为MP4格式:详细代码示例在日常的网页制作过程中,我们常常会遇到将HTML页面或者特定的HTML元素转换为MP4视频的需求。例如将动画效果、幻灯片或其他动态元素保存为视频文件。本文将介绍如何使用HTML5和JavaScript将HTML转换为MP4格式,并提供具体的代码示例。HTML5的video标签和CanvasAPIHTML5引入
 调用SQL触发器执行外部程序
Feb 18, 2024 am 10:25 AM
调用SQL触发器执行外部程序
Feb 18, 2024 am 10:25 AM
标题:SQL触发器调用外部程序的具体代码示例正文:在使用SQL触发器时,有时候需要调用外部程序来处理一些特定的操作。本文将介绍如何在SQL触发器中调用外部程序,并给出具体的代码示例。一、创建触发器首先,我们需要创建一个触发器来监听数据库中的某个事件。这里以“订单表(order_table)”为例,当有新的订单被插入时,触发器就会被激活,然后调用外部程序进行一
 提取Dump文件的方法
Feb 19, 2024 pm 12:15 PM
提取Dump文件的方法
Feb 19, 2024 pm 12:15 PM
抓取Dump文件的方法在计算机系统中,Dump文件是一个记录系统运行状态和数据的文件。在软件开发和系统故障排查中,抓取Dump文件可以帮助程序开发人员和系统管理员分析和诊断各种问题,例如程序崩溃、内存泄漏以及系统异常等。本文将介绍一些常见的方法和工具来抓取Dump文件。一、Windows系统下抓取Dump文件的方法使用任务管理器:在Windows操作系统中,
 Windows 12发布日期
Jan 05, 2024 pm 05:24 PM
Windows 12发布日期
Jan 05, 2024 pm 05:24 PM
此前win11正式发布,让不少用户已经开始畅享win12了,想知道win12什么时候发布的,其实根据规律来看它将在2024年左右发布。win12什么时候发布的:答:win12预计在2024年秋季左右发布。1、根据微软最新的爆料信息来看,win12预计会在2024秋季进行发布。2、并且这一次的win12将会有多个全新的设计理念,在整洁视觉上会有更多的提升。3、最新的开发者会上,微软的开发员工就爆料将要制作一个浮动的任务栏,让任务栏有一种浮动的感觉。
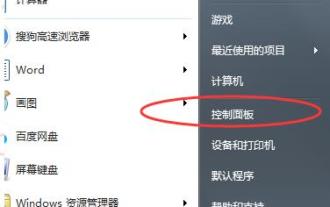 如何调整Windows 7桌面显示比例
Dec 27, 2023 am 08:13 AM
如何调整Windows 7桌面显示比例
Dec 27, 2023 am 08:13 AM
使用win7的小伙伴非常的多,在电脑上看视频或是资料的时候都会需要进行比例的调整吧,那么该怎么去调整呢?下面就来看看详细的设置方法吧。win7桌面显示比例怎么设置:1、点击左下角电脑打开“控制面板”。2、随后在控制面板中找到“外观”。3、进入外观后点击“显示”。4、随后即可根据需要显示的效果进行桌面的大小显示调节。5、也可以点击左侧的“调整分辨率”。6、通过更改屏幕分辨率来调整电脑桌面的比例。
 NVIDIA控制面板的作用是什么?
Feb 19, 2024 pm 03:59 PM
NVIDIA控制面板的作用是什么?
Feb 19, 2024 pm 03:59 PM
NVIDIA控制面板是干嘛的随着计算机科技发展的日新月异,显卡的重要性变得越来越大。而NVIDIA作为全球著名的显卡制造商之一,其控制面板更是备受瞩目。那么,NVIDIA控制面板究竟是干什么的呢?本文将为大家详细介绍NVIDIA控制面板的功能和用途。首先,我们来了解NVIDIA控制面板的概念与定义。NVIDIA控制面板是一种用于管理和配置显卡相关设置的软件。
 全角和半角在中文输入法中的作用
Mar 25, 2024 am 09:57 AM
全角和半角在中文输入法中的作用
Mar 25, 2024 am 09:57 AM
全角和半角是在中文输入法中常见的概念,它们分别代表了不同的字符宽度。在计算机领域中,全角和半角的概念主要用于描述汉字和英文字母在屏幕或打印上所占用的空间大小。首先,全角和半角最初起源于打字机时代。在打字机上,中文字符通常采用全角形式显示,而英文字符则采用半角形式显示。这是因为中文字符相对较宽,使用全角可以使得整篇文章看起来更加美观,排版更加紧凑。而英文字符相






