将给定的二叉搜索树中的所有较大值添加到每个节点中
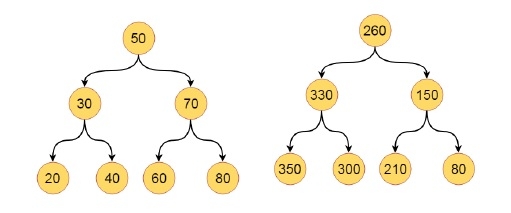
在这里我们将看到一个有趣的问题,我们将为一个给定的二叉搜索树中的每个节点添加更大的值。因此,初始和最终的树将如下所示 -
算法
bstUpdate(root, sum) -
Begin if root is null, then stop bstUpdate(right of room, sum) sum := sum + value of root update root value using sum bstUpdate(left of room, sum) End
示例
#include<iostream>
using namespace std;
class Node {
public:
int data;
Node *left, *right;
};
Node *getNode(int item) {
Node *newNode = new Node();
newNode->data = item;
newNode->left = newNode->right = NULL;
return newNode;
}
void updateBST(Node *root, int *sum) {
if (root == NULL)
return;
updateBST(root->right, sum); //update right sub tree
*sum = *sum + root->data;
root->data = *sum; //update root data
updateBST(root->left, sum); //update left sub tree
}
void BSTUpdate(Node *root) {
int sum = 0;
updateBST(root, &sum);
}
void inorder(Node *root) {
if (root != NULL) {
inorder(root->left);
cout<<root->data<<" ";
inorder(root->right);
}
}
Node* insert(Node* node, int data) {
if (node == NULL)
return getNode(data);
if (data <= node->data) //go to left
node->left = insert(node->left, data);
else //go to right
node->right = insert(node->right, data);
return node;
}
int main() {
int data[] = {50, 30, 20, 40, 70, 60, 80};
int n = sizeof(data)/sizeof(data[0]);
Node *root = NULL;
for(int i = 0; i < n; i++) {
root = insert(root, data[i]);
}
BSTUpdate(root);
inorder(root);
}输出
350 330 300 260 210 150 80
以上是将给定的二叉搜索树中的所有较大值添加到每个节点中的详细内容。更多信息请关注PHP中文网其他相关文章!

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

Video Face Swap
使用我们完全免费的人工智能换脸工具轻松在任何视频中换脸!

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)
 使用队列反转二叉搜索树中的路径的C++代码
Sep 14, 2023 pm 07:21 PM
使用队列反转二叉搜索树中的路径的C++代码
Sep 14, 2023 pm 07:21 PM
例如,给定一个二叉搜索树,我们需要从特定键反转其路径。寻找解决方案的方法在这种方法中,我们将创建一个队列并推送所有节点,直到获得根节点。p>示例 #include<bits/stdc++.h>usingnamespacestd;structnode{ intkey; structnode*left,*right;};structnode*newNode(intitem){&nb
 C++中的二叉堆和二叉搜索树
Aug 22, 2023 pm 04:10 PM
C++中的二叉堆和二叉搜索树
Aug 22, 2023 pm 04:10 PM
在C++编程中,二叉堆和二叉搜索树是两种常用的数据结构,它们具有相似之处,但是也有着不同点。本文将分别介绍二叉堆和二叉搜索树的概念、基本操作及其应用场景。一、二叉堆1.1概念二叉堆是一种完全二叉树,满足以下两种性质:1.1.1堆序性堆序性指在一个二叉堆中,每个节点的值都不大于(或不小于)其父节点的值。这里以最大堆为例,即根节点的值是整个树中最大的值,而
 Python中如何实现二叉搜索树
Jun 10, 2023 am 08:57 AM
Python中如何实现二叉搜索树
Jun 10, 2023 am 08:57 AM
二叉搜索树(BinarySearchTree,BST)是一种基于二叉树的搜索算法。它的特点是在树中每个节点的左子树中的值都小于这个节点的值,而右子树中的值则大于这个节点的值。因此,BST的搜索和插入操作的时间复杂度是O(logN)。在Python中实现二叉搜索树的方法比较简单,因为Python内置了列表和字典这两种数据结构,它们都可以用来实现二叉树。在这
 Java利用Math类的max()函数获取两个数中的较大值
Jul 24, 2023 pm 11:17 PM
Java利用Math类的max()函数获取两个数中的较大值
Jul 24, 2023 pm 11:17 PM
Java利用Math类的max()函数获取两个数中的较大值在Java编程中,我们经常需要比较两个数的大小,然后选择较大的数进行一些操作。Java中的Math类提供了许多数学运算的函数,其中max()函数可以帮助我们获取两个数中的较大值。Math.max()函数的定义如下:publicstaticintmax(inta,intb)该函数接受两个整数
 如何使用C#编写二叉搜索树算法
Sep 19, 2023 pm 01:03 PM
如何使用C#编写二叉搜索树算法
Sep 19, 2023 pm 01:03 PM
如何使用C#编写二叉搜索树算法,需要具体代码示例二叉搜索树(BinarySearchTree,简称BST)是一种常用的数据结构,它具有快速地插入、查找和删除操作的特点。在C#中,我们可以使用面向对象的方式来编写二叉搜索树算法。首先,我们需要定义一个二叉搜索树节点的类,其中包含一个值和两个指向左右子节点的指针。代码如下所示:publicclassBST
 如何使用java实现二叉搜索树算法
Sep 19, 2023 am 08:48 AM
如何使用java实现二叉搜索树算法
Sep 19, 2023 am 08:48 AM
如何使用Java实现二叉搜索树算法二叉搜索树(BinarySearchTree,简称BST)是一种常用的数据结构,能够高效地实现插入、删除和查找等操作。本文将介绍如何使用Java来实现二叉搜索树,并提供相应的代码示例。一、二叉搜索树的定义二叉搜索树是一种有序树,具有以下特点:每个节点都有一个唯一的键值。左子树的键值小于节点的键值,右子树的键值大于节点的键
 将给定的二叉搜索树中的所有较大值添加到每个节点中
Sep 16, 2023 pm 08:45 PM
将给定的二叉搜索树中的所有较大值添加到每个节点中
Sep 16, 2023 pm 08:45 PM
在这里我们将看到一个有趣的问题,我们将为一个给定的二叉搜索树中的每个节点添加更大的值。因此,初始和最终的树将如下所示-算法bstUpdate(root,sum)-Begin ifrootisnull,thenstop bstUpdate(rightofroom,sum) sum:=sum+valueofroot updaterootvalueus
 将给定二叉搜索树中的所有较大值添加到每个节点上
Sep 07, 2023 pm 12:17 PM
将给定二叉搜索树中的所有较大值添加到每个节点上
Sep 07, 2023 pm 12:17 PM
BST或二叉搜索树是一种二叉树形式,其中所有左节点的值小于根节点的值,所有右节点的值大于根节点的值。对于这个问题,我们将取一个二叉树并将所有大于当前节点值的值添加到它中。问题“向BST的每个节点添加所有较大的值”被简化为对于BST,将所有大于当前节点值的节点值添加到该节点值。向BST中的每个节点添加所有较大的值问题陈述:给定一个二叉搜索树(BST),我们需要为每个节点添加所有较大值节点的总和。输入 10 /&nb






