重温图灵原理,感受反证法的力量
算法已经无处不在,似乎对于每一个可以用精确的数学术语表达的问题,都有相应的算法。然而,事实并非如此,实际上有些看似简单的问题永远无法通过算法解决
计算机科学家中的先驱艾伦・图灵,曾在近一个世纪前的一篇论文中证明了这种「不可计算」问题的存在,他提出了启动现代计算机科学的计算数学模型。
图灵用一种违反直觉的策略证明了这一突破性的结果:他定义了一个问题,一个拒绝一切试图解决它的方法的问题。「比如我问你在做什么,不管你回答什么我都会说,'我要做的事情和你说的不一样'。」麻省理工学院研究理论计算机科学的研究生 Rahul Ilango 说。 重写后的内容: 图灵以一种违反直觉的策略证明了这一突破性的结果:他定义了一个问题,这个问题拒绝一切试图解决它的方法。「比如我问你在做什么,不管你回答什么我都会说,'我要做的事情和你说的不一样'。」麻省理工学院研究理论计算机科学的研究生Rahul Ilango表示
图灵的策略是基于一种具有悠久历史的数学方法,被称为「对角线证明」。下面是对他证明背后逻辑的简化说明
字符串
对角线证明源于解决一个关于字符串问题的巧妙技巧,字符串中每个比特位的值可以是 0 或 1。该问题的描述是:给定一个字符串列表,列表中所有字符串都一样长,如何能生成一个不在列表中的新字符串呢?
重写后的内容:一种最直接的策略是按顺序考虑每个可能的字符串。假设有五个字符串,每个字符串都有五位。首先遍历检查列表中是否存在00000。如果不存在,问题就解决了;如果存在,则转到00001并重复这个过程。这种方法很简单,但对于长字符串所产生的长列表来说速度很慢
对角线证明是一种可行的替代方法,可以逐步构建不存在的字符串。从列表中第一个字符串的第一位开始,将其反转,这将成为新字符串的第一位。然后反转第二个字符串的第二位,并将其作为新字符串的第二位,重复此操作,直到到达列表的末尾。通过反转位的操作,可以确保新字符串与原始列表中的每个字符串至少有一个不同的位置。(它们还在字符串列表中形成一条对角线,因此被称为对角线证明。)
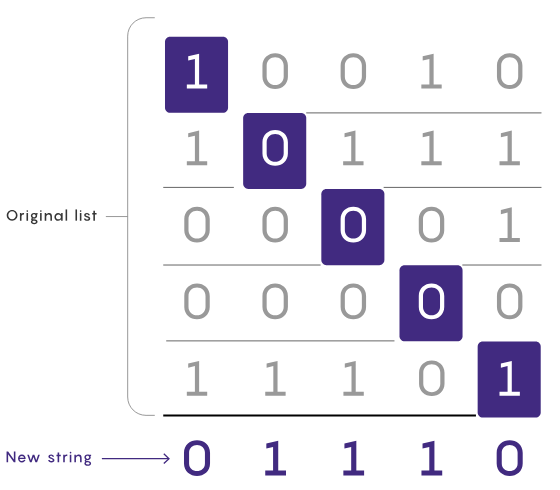
对角线证明只需要依次检查列表中每个字符串中的一位,所以通常比其他方法快得多,但它真正的威力在于它能很好地驾驭无限长的字符串问题。
麻省理工学院的理论计算机科学家 Ryan Williams 表示:“虽然字符串和列表可以是无限的,但对角化方法仍然是有效的。”
乔治·康托尔是第一个利用这种力量的人,他是集合论数学领域的创始人。1873年,他利用对角线证明了一些无穷大的值比其他的更大。60年后,图灵将这一版本的对角线证明应用于计算理论
算法的限制性
为了证明存在一类数学问题是无法通过任何算法解决的,图灵提出了一个理论。这类问题具有明确定义的输入和输出,但没有确定的过程可以将输入转化为输出。图灵主要关注决策问题,并为了更好地具象化这个模糊的任务。在决策问题中,输入可以是由0和1组成的任意字符串,而输出则可以是0或1
确定一个数字是否是素数(只能被 1 和它本身整除)是决策问题的一个例子 —— 给定一个代表数字的输入字符串,如果该数字是素数,则正确的输出为 1,如果不是素数,则为 0。另一个例子是检查计算机程序的语法错误。输入字符串代表不同程序的代码 —— 所有程序都可以用这种方式表示,因为这就是它们在计算机上存储和执行的方式 —— 规则是如果代码包含语法错误,则输出 1,如果不包含,则输出 0。
只有当算法为每一个可能的输入都产生正确的输出时,它才能说是可以解决该问题 —— 哪怕失败一次,它就不是解决该问题的通用算法。通常,人们会先指定一个想解决的问题,然后试图找到一个解决它的算法。图灵在寻找无法解决的问题时,颠覆了这一逻辑 —— 他想象了一个包含所有可能算法的无限列表,并使用对角化来构造一个难题,这个难题与列表上的每一个算法都对立。
请设想一个由20个问题组成的新问题,回答者不是从一个具体的概念出发,而是依次对每个问题都想出一个不满足的例子。当游戏结束时,回答者已经描述了一个完全由问题对立面所组成的命题
图灵的对角线证明过程,就是要在无限长的算法列表中,对每一个算法都进行思考:「这个算法能解决我们想要证明是不可计算的问题吗?」,就好像是一种游戏比赛。Williams 表示:「这种方式将原来的问题转化为一种『无限的问题』。」
为了赢得游戏,图灵需要设计一个问题,对于每个算法给出的答案都是否定的。这意味着需要找出使第一个算法输出错误答案的特定输入,另一个使第二个算法失败的输入,以此类推。他发现,这些特殊输入使用了类似于库尔特・哥德尔 (Kurt Gödel) 在不久前在证明像「这个命题是不可证明的」这样的自我引用断言会给数学基础带来麻烦时,所使用的技巧。
此处的关键在于,每个算法(或程序)都可以表示为 0 和 1 的字符串。这意味着,就像在错误检查程序的例子中一样,算法可以将另一个算法的编码作为输入。原则上,算法甚至可以将自己的编码作为输入。
这样一来,我们可以定义一个不可计算的问题,就像在图灵证明中所提到的问题一样:“给定一个表示算法代码的输入字符串,当算法自身的代码作为输入时,如果该算法输出0,则让其输出1,否则输出0。”每个试图解决这个问题的算法都会在至少一个输入上产生错误的输出,即与自己的代码对应的输入。这意味着这个反常的问题无法用任何算法来解决
证明不了什么的是反证法
计算机科学家对于对角线证明的使用并没有到此结束。1965 年,Juris Hartmanis 和 Richard Stearns 改编了图灵的论点,以证明并非所有可计算问题是平等的 —— 有些问题本质上比其他问题更难。这一结果启动了计算复杂性理论领域,研究计算问题的难度。
复杂性理论的发展揭示了图灵对角线证明的局限性。在1975年,贝克、吉尔和索洛维证明了复杂性理论中许多未解决的问题无法仅通过对角化来解决。其中最重要的是著名的P/NP问题,该问题简单来说是关于能否在多项式时间内验证解的正确性以及是否能在多项式时间内求解的问题
对角线证明的局限性是使其如此强大的高抽象水平的直接结果。图灵的证明并没有涉及任何在实践中可能出现的不可计算的问题 —— 相反,问题往往是抽象的。其他对角线证明同样远离现实世界,因此它们无法解决现实世界中的问题。
Williams 说:「对角线证明并不是直接触碰问题本身,就好像用手套箱做实验一样。」
对角线证明的颓败之势,表明解决 P/NP 问题将是一个漫长的旅程。尽管存在局限性,对角线证明仍然是复杂性理论家武器库中的关键工具之一。2011 年,威廉姆斯将其与一系列其他技术结合起来,证明了某个受限制的计算模型无法解决一些异常困难的问题 —— 这一结果让困扰了研究人员 25 年的问题得到解决。虽然这与解决 P/NP 问题相去甚远,但仍然代表着重大进展。
如果你想证明某些事情是不可能的,不要低估否定的力量
原文链接:
需要重写的内容是:https://www.quantamagazine.org/alan-turing-and-the-power-of-negative-thinking-20230905/
以上是重温图灵原理,感受反证法的力量的详细内容。更多信息请关注PHP中文网其他相关文章!

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

Video Face Swap
使用我们完全免费的人工智能换脸工具轻松在任何视频中换脸!

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)
 一键生成PPT!Kimi :让「PPT民工」先浪起来
Aug 01, 2024 pm 03:28 PM
一键生成PPT!Kimi :让「PPT民工」先浪起来
Aug 01, 2024 pm 03:28 PM
Kimi:一句话,十几秒钟,一份PPT就新鲜出炉了。PPT这玩意儿,可太招人烦了!开个碰头会,要有PPT;写个周报,要做PPT;拉个投资,要展示PPT;就连控诉出轨,都得发个PPT。大学更像是学了个PPT专业,上课看PPT,下课做PPT。或许,37年前丹尼斯・奥斯汀发明PPT时也没想到,有一天PPT竟如此泛滥成灾。吗喽们做PPT的苦逼经历,说起来都是泪。「一份二十多页的PPT花了三个月,改了几十遍,看到PPT都想吐」;「最巅峰的时候,一天做了五个PPT,连呼吸都是PPT」;「临时开个会,都要做个
 值得你花时间看的扩散模型教程,来自普渡大学
Apr 07, 2024 am 09:01 AM
值得你花时间看的扩散模型教程,来自普渡大学
Apr 07, 2024 am 09:01 AM
Diffusion不仅可以更好地模仿,而且可以进行「创作」。扩散模型(DiffusionModel)是一种图像生成模型。与此前AI领域大名鼎鼎的GAN、VAE等算法,扩散模型另辟蹊径,其主要思想是一种先对图像增加噪声,再逐步去噪的过程。其中如何去噪还原原图像是算法的核心部分。最终算法能够从一张随机的噪声图像中生成图像。近年来,生成式AI的惊人增长将文本转换为图像生成、视频生成等领域的许多令人兴奋的应用提供了支持。这些生成工具背后的基本原理是扩散的概念,这是一种特殊的采样机制,克服了以前的方法中被
 CVPR 2024全部奖项公布!近万人线下参会,谷歌华人研究员获最佳论文奖
Jun 20, 2024 pm 05:43 PM
CVPR 2024全部奖项公布!近万人线下参会,谷歌华人研究员获最佳论文奖
Jun 20, 2024 pm 05:43 PM
北京时间6月20日凌晨,在西雅图举办的国际计算机视觉顶会CVPR2024正式公布了最佳论文等奖项。今年共有10篇论文获奖,其中2篇最佳论文,2篇最佳学生论文,另外还有2篇最佳论文提名和4篇最佳学生论文提名。计算机视觉(CV)领域的顶级会议是CVPR,每年都会吸引大量研究机构和高校参会。据统计,今年共提交了11532份论文,2719篇被接收,录用率为23.6%。根据佐治亚理工学院对CVPR2024的数据统计分析,从研究主题来看,论文数量最多的是图像和视频合成与生成(Imageandvideosyn
 从裸机到700亿参数大模型,这里有份教程,还有现成可用的脚本
Jul 24, 2024 pm 08:13 PM
从裸机到700亿参数大模型,这里有份教程,还有现成可用的脚本
Jul 24, 2024 pm 08:13 PM
我们知道LLM是在大规模计算机集群上使用海量数据训练得到的,本站曾介绍过不少用于辅助和改进LLM训练流程的方法和技术。而今天,我们要分享的是一篇深入技术底层的文章,介绍如何将一堆连操作系统也没有的「裸机」变成用于训练LLM的计算机集群。这篇文章来自于AI初创公司Imbue,该公司致力于通过理解机器的思维方式来实现通用智能。当然,将一堆连操作系统也没有的「裸机」变成用于训练LLM的计算机集群并不是一个轻松的过程,充满了探索和试错,但Imbue最终成功训练了一个700亿参数的LLM,并在此过程中积累
 PyCharm社区版安装指南:快速掌握全部步骤
Jan 27, 2024 am 09:10 AM
PyCharm社区版安装指南:快速掌握全部步骤
Jan 27, 2024 am 09:10 AM
快速入门PyCharm社区版:详细安装教程全解析导言:PyCharm是一个功能强大的Python集成开发环境(IDE),它提供了一套全面的工具,可以帮助开发人员更高效地编写Python代码。本文将详细介绍如何安装PyCharm社区版,并提供具体的代码示例,帮助初学者快速入门。第一步:下载和安装PyCharm社区版要使用PyCharm,首先需要从其官方网站上下
 AI在用 | AI制作独居女孩生活Vlog,3天狂揽上万点赞量
Aug 07, 2024 pm 10:53 PM
AI在用 | AI制作独居女孩生活Vlog,3天狂揽上万点赞量
Aug 07, 2024 pm 10:53 PM
机器之能报道编辑:杨文以大模型、AIGC为代表的人工智能浪潮已经在悄然改变着我们生活及工作方式,但绝大部分人依然不知道该如何使用。因此,我们推出了「AI在用」专栏,通过直观、有趣且简洁的人工智能使用案例,来具体介绍AI使用方法,并激发大家思考。我们也欢迎读者投稿亲自实践的创新型用例。视频链接:https://mp.weixin.qq.com/s/2hX_i7li3RqdE4u016yGhQ最近,独居女孩的生活Vlog在小红书上走红。一个插画风格的动画,再配上几句治愈系文案,短短几天就能轻松狂揽上
 技术入门者必看:C语言和Python难易程度解析
Mar 22, 2024 am 10:21 AM
技术入门者必看:C语言和Python难易程度解析
Mar 22, 2024 am 10:21 AM
标题:技术入门者必看:C语言和Python难易程度解析,需要具体代码示例在当今数字化时代,编程技术已成为一项越来越重要的能力。无论是想要从事软件开发、数据分析、人工智能等领域,还是仅仅出于兴趣学习编程,选择一门合适的编程语言是第一步。而在众多编程语言中,C语言和Python作为两种广泛应用的编程语言,各有其特点。本文将对C语言和Python的难易程度进行解析
 细数RAG的12个痛点,英伟达高级架构师亲授解决方案
Jul 11, 2024 pm 01:53 PM
细数RAG的12个痛点,英伟达高级架构师亲授解决方案
Jul 11, 2024 pm 01:53 PM
检索增强式生成(RAG)是一种使用检索提升语言模型的技术。具体来说,就是在语言模型生成答案之前,先从广泛的文档数据库中检索相关信息,然后利用这些信息来引导生成过程。这种技术能极大提升内容的准确性和相关性,并能有效缓解幻觉问题,提高知识更新的速度,并增强内容生成的可追溯性。RAG无疑是最激动人心的人工智能研究领域之一。有关RAG的更多详情请参阅本站专栏文章《专补大模型短板的RAG有哪些新进展?这篇综述讲明白了》。但RAG也并非完美,用户在使用时也常会遭遇一些「痛点」。近日,英伟达生成式AI高级解决






