揭示了「原子几何」的奥秘:机器学习在推动数学领域的发展
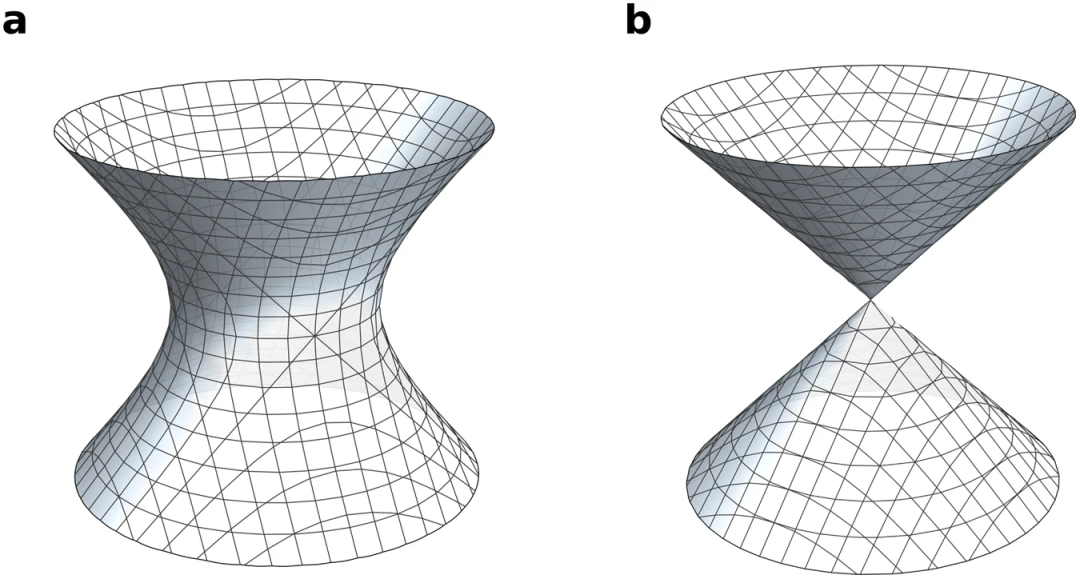
代数簇是一个由多个多项式方程定义的集合。它是代数几何学中的重要概念,研究了多项式方程的解集合在几何空间中的性质。代数簇的方程可以是任意维度的,可以是实数域上的方程,也可以是复数域上的方程。研究代数簇的性质可以帮助我们理解多项式方程的根的分布和几何形态
代数几何是将代数和几何两个数学分支融合在一起的学科。一方面,它涉及到代数,即研究方程的性质和解法;另一方面,它也涉及到几何,即研究形状的性质和特征。代数几何的目标就是将抽象的代数方法应用到几何中,解决与复杂具体的形状、曲面、空间和曲线相关的问题
代数几何的基本问题是对一组多项式方程的解集进行分类,简单说来就是对空间进行分类。其研究的基本对象名为代数簇(Algebraic variety),也就是多项式方程组的解集的几何表示。
而法诺簇(Fano variety)是一类重要的代数簇。从某种意义上说,它们是数学形状的「原子片段」(Atomic pieces)。法诺簇在弦理论中也起着重要的作用。
重写后的内容:法诺簇是几何形状的基本构建块,它们是数学形状的「原子块」。最新的法诺簇分类研究包括分析一种被称为量子周期的不变性。量子周期是一系列整数,用于为法诺簇提供数值指纹。据猜测,法诺簇的几何特性可以直接从其量子周期恢复,如果这一假设成立的话
最近,来自诺丁汉大学和伦敦帝国学院的数学家们首次利用机器学习来扩展和加速对「原子形状」的研究。这些「原子形状」是构成更高维度基本几何形状的组成部分
具体而言,研究人员将机器学习应用于一个问题:X 的量子周期是否知道 X 的维度?请注意,尚无对此的理论理解。研究表明,简单的前馈神经网络可以以 98% 的精度确定 X 的维度。在此基础上,研究人员在一类法诺簇的量子周期内建立了严格的渐近性。这些渐近性决定了 X 的量子周期的维度。结果表明,在缺乏理论理解的情况下,机器学习可以从复杂的数学数据中挑选结构。他们还为猜想提供了积极的证据,即法诺簇的量子周期决定了多样性。
该研究题为《机器学习范诺多样性的维度》,于2023年9月8日在《自然通讯》上发布

论文链接:https://www.nature.com/articles/s41467-023-41157-1
几年前,该研究小组开始了创建形状元素周期表的研究。他们将原子碎片称为法诺簇。该团队将一组称为量子周期的数字序列与每个形状相关联,以提供描述形状的「条形码」或「指纹」。最近,他们通过使用一种新的机器学习方法,成功地快速筛选这些条形码,从而能够识别形状及其属性,例如每个形状的尺寸
Alexander Kasprzyk 说:「对于数学家来说,关键步骤是确定在给定问题中的模式。这可能非常困难,一些数学理论可能需要数年的时间才能发现。」
Tom Coates 教授说:「这是人工智能可以真正彻底改变数学的地方,因为我们已经证明机器学习是在代数和几何等复杂领域中发现模式的强大工具。」
Sara Veneziale 说:「我们对可以在纯数学中使用机器学习的事实感到非常兴奋。这将加速整个领域的新见解。」
总的来说,这项研究表明,机器学习能够在复杂的数学数据中发现以前未知的结构,并且是开发严格数学结果的强大工具。它还为法诺簇程序中的基本猜想提供了证据:法诺簇的正则量子周期决定了这种变化
以上是揭示了「原子几何」的奥秘:机器学习在推动数学领域的发展的详细内容。更多信息请关注PHP中文网其他相关文章!

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

热门话题
 mysql 无法启动怎么解决
Apr 08, 2025 pm 02:21 PM
mysql 无法启动怎么解决
Apr 08, 2025 pm 02:21 PM
MySQL启动失败的原因有多种,可以通过检查错误日志进行诊断。常见原因包括端口冲突(检查端口占用情况并修改配置)、权限问题(检查服务运行用户权限)、配置文件错误(检查参数设置)、数据目录损坏(恢复数据或重建表空间)、InnoDB表空间问题(检查ibdata1文件)、插件加载失败(检查错误日志)。解决问题时应根据错误日志进行分析,找到问题的根源,并养成定期备份数据的习惯,以预防和解决问题。
 偏远的高级后端工程师(平台)需要圈子
Apr 08, 2025 pm 12:27 PM
偏远的高级后端工程师(平台)需要圈子
Apr 08, 2025 pm 12:27 PM
远程高级后端工程师职位空缺公司:Circle地点:远程办公职位类型:全职薪资:$130,000-$140,000美元职位描述参与Circle移动应用和公共API相关功能的研究和开发,涵盖整个软件开发生命周期。主要职责独立完成基于RubyonRails的开发工作,并与React/Redux/Relay前端团队协作。为Web应用构建核心功能和改进,并在整个功能设计过程中与设计师和领导层紧密合作。推动积极的开发流程,并确定迭代速度的优先级。要求6年以上复杂Web应用后端
 mysql 能返回 json 吗
Apr 08, 2025 pm 03:09 PM
mysql 能返回 json 吗
Apr 08, 2025 pm 03:09 PM
MySQL 可返回 JSON 数据。JSON_EXTRACT 函数可提取字段值。对于复杂查询,可考虑使用 WHERE 子句过滤 JSON 数据,但需注意其性能影响。MySQL 对 JSON 的支持在不断增强,建议关注最新版本及功能。
 了解 ACID 属性:可靠数据库的支柱
Apr 08, 2025 pm 06:33 PM
了解 ACID 属性:可靠数据库的支柱
Apr 08, 2025 pm 06:33 PM
数据库ACID属性详解ACID属性是确保数据库事务可靠性和一致性的一组规则。它们规定了数据库系统处理事务的方式,即使在系统崩溃、电源中断或多用户并发访问的情况下,也能保证数据的完整性和准确性。ACID属性概述原子性(Atomicity):事务被视为一个不可分割的单元。任何部分失败,整个事务回滚,数据库不保留任何更改。例如,银行转账,如果从一个账户扣款但未向另一个账户加款,则整个操作撤销。begintransaction;updateaccountssetbalance=balance-100wh
 掌握SQL LIMIT子句:控制查询中的行数
Apr 08, 2025 pm 07:00 PM
掌握SQL LIMIT子句:控制查询中的行数
Apr 08, 2025 pm 07:00 PM
SQLLIMIT子句:控制查询结果行数SQL中的LIMIT子句用于限制查询返回的行数,这在处理大型数据集、分页显示和测试数据时非常有用,能有效提升查询效率。语法基本语法:SELECTcolumn1,column2,...FROMtable_nameLIMITnumber_of_rows;number_of_rows:指定返回的行数。带偏移量的语法:SELECTcolumn1,column2,...FROMtable_nameLIMIToffset,number_of_rows;offset:跳过
 Bangla 部分模型检索中的 Laravel Eloquent ORM)
Apr 08, 2025 pm 02:06 PM
Bangla 部分模型检索中的 Laravel Eloquent ORM)
Apr 08, 2025 pm 02:06 PM
LaravelEloquent模型检索:轻松获取数据库数据EloquentORM提供了简洁易懂的方式来操作数据库。本文将详细介绍各种Eloquent模型检索技巧,助您高效地从数据库中获取数据。1.获取所有记录使用all()方法可以获取数据库表中的所有记录:useApp\Models\Post;$posts=Post::all();这将返回一个集合(Collection)。您可以使用foreach循环或其他集合方法访问数据:foreach($postsas$post){echo$post->
 如何针对高负载应用程序优化 MySQL 性能?
Apr 08, 2025 pm 06:03 PM
如何针对高负载应用程序优化 MySQL 性能?
Apr 08, 2025 pm 06:03 PM
MySQL数据库性能优化指南在资源密集型应用中,MySQL数据库扮演着至关重要的角色,负责管理海量事务。然而,随着应用规模的扩大,数据库性能瓶颈往往成为制约因素。本文将探讨一系列行之有效的MySQL性能优化策略,确保您的应用在高负载下依然保持高效响应。我们将结合实际案例,深入讲解索引、查询优化、数据库设计以及缓存等关键技术。1.数据库架构设计优化合理的数据库架构是MySQL性能优化的基石。以下是一些核心原则:选择合适的数据类型选择最小的、符合需求的数据类型,既能节省存储空间,又能提升数据处理速度
 mysql 主键可以为 null
Apr 08, 2025 pm 03:03 PM
mysql 主键可以为 null
Apr 08, 2025 pm 03:03 PM
MySQL 主键不可以为空,因为主键是唯一标识数据库中每一行的关键属性,如果主键可以为空,则无法唯一标识记录,将会导致数据混乱。使用自增整型列或 UUID 作为主键时,应考虑效率和空间占用等因素,选择合适的方案。






