以3D视角洞悉矩阵乘法,这就是AI思考的样子
如果能以 3D 方式展示矩阵乘法的执行过程,当年学习矩阵乘法时也就不会那么吃力了。
现如今,矩阵乘法已经成为机器学习模型的构建模块,是各种强大 AI 技术的基础,了解其执行方式必然有助于我们更深入地理解这个 AI 以及这个日趋智能化的世界。
这篇来自 PyTorch 博客的文章将介绍一种用于矩阵乘法和矩阵乘法组合的可视化工具 mm。
因为 mm 使用了所有三个空间维度,所以相比于通常的二维图表,mm 有助于直觉化的展示和激发思路,所使用的认知开销也更小,尤其是(但不限于)对于擅长视觉和空间思考的人。
而且如果有三个维度来组合矩阵乘法,再加上加载已训练权重的能力,mm 能可视化大型复合表达式(如注意力头)并观察它们的实际行为模式。
mm 是完全交互式的,运行在浏览器或笔记本 iframe 中,并且其会将完整状态保存在 URL 中,因此链接就是可共享的会话(本文中的截图和视频都有一个链接,可在该工具中打开对应的可视化,具体请参看原博客)。本参考指南会描述所有可用的功能。
工具地址:https://bhosmer.github.io/mm/ref.html
博客原文:https://pytorch.org/blog/inside-the-matrix
本文首先会介绍可视化方法,通过可视化一些简单矩阵乘法和表达式来建立直觉,然后再深入一些扩展示例:
介绍:为什么这种可视化方式更好?
热身:动画 —— 查看规范的矩阵乘法分解的工作过程
热身:表达式 —— 速览一些基本的表达式构建模块
深入注意力头:通过 NanoGPT 深度观察 GPT-2 的一对注意力头的结构、值和计算行为
并行化注意力:使用来自近期的 Blockwise Parallel Transformer 论文中的示例可视化注意力头的并行化。
注意力层的大小:当我们将整个注意力层可视化为单个结构,则注意力层的 MHA 半边和 FFA 半边合起来是什么样子?在自回归解码过程中,其图像会发生怎样的变化?
LoRA:对这种注意力头架构的详细阐释的可视化解释
1 介绍
mm 的可视化方法基于这一前提:矩阵乘法本质上是一种三维运算。
换句话说:
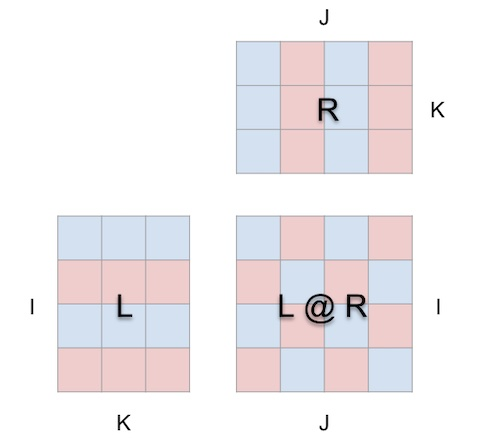
其实可以描绘成这种形式:

当我们以这种方式将矩阵乘法包裹在一个立方体中时,参数形状、结果形状和共享维度之间的正确关系就全部就位了。
现在矩阵乘法计算就有了几何意义:结果矩阵中的每个位置 i,j 都锚定了一个沿立方体内部的深度(depth)维度 k 运行的向量,其中从 L 的第 i 行延伸出来的水平面与从 R 的第 j 列延伸出来的垂直面相交。沿着这一向量,来自左边参数和右边参数的成对的 (i, k) (k, j) 元素会相遇并相乘,再沿 k 对所得积求和,所得结果放入结果的 i, j 位置。
这就是矩阵乘法的直观含义:
1. 将两个正交矩阵投影到一个立方体的内部;
2. 将每个交叉点的一对值相乘,得到一个乘积网格;
3. 沿第三个正交维度进行求和,以生成结果矩阵。
对于方向,该工具会在立方体内部显示一个指向结果矩阵的箭头,其中蓝色箭羽来自左侧参数,红色箭羽来自右侧参数。该工具还会显示白色指示线来指示每个矩阵的行轴线,尽管这些线在此截图中很模糊。
其布局约束条件简单又直接:
左侧参数和结果必须沿它们共享的高度 (i) 维度邻接
右侧参数和结果必须沿它们共享的宽度 (j) 维度邻接
左侧参数和右侧参数必须沿它们共享的(左宽度 / 右高度)维度邻接,该维度成为矩阵乘法的深度 (k) 维度
这种几何表示方法能为可视化所有标准的矩阵乘法分解提供坚实的基础,并能为探索非平凡的复杂矩阵乘法组合提供直观的基础,接下来我们就能看到这一点。
2 热身:动画
在深入介绍更复杂的示例之前,我们先来看看这种可视化风格看起来是什么样的,从而建立起对该工具的直觉认知。
2a 点积
首先来看一个经典算法 —— 通过计算对应左侧行和右侧列的点积来计算每个结果元素。从这里的动画可以看到,相乘的值向量扫过立方体内部,每一次都在相应位置提交一个求和后的结果。
这里,L 具有填充有 1(蓝色)或 -1(红色)的行块;R 具有类似填充的列块。这里 k 是 24,所以结果矩阵 (L @ R) 的蓝色值为 24,红色值为 -24。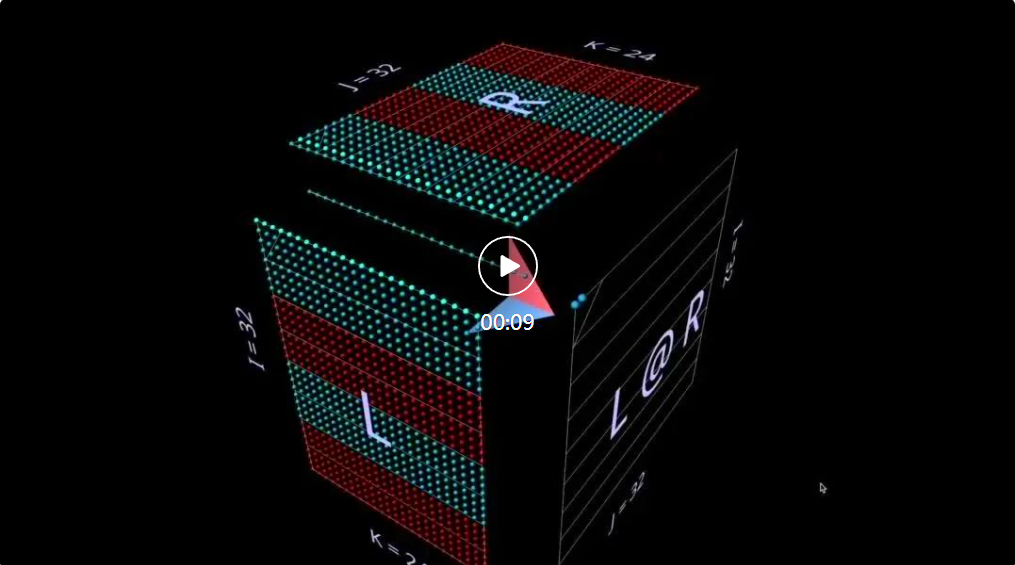
2b 矩阵 - 向量积
分解为矩阵 - 向量积的矩阵乘法看起来像一个垂直平面(左侧参数与右侧参数每一列的积),当它水平扫过立方体内部时,将列绘制到结果上:
观察一个分解的中间值可能很有意思,即使示例很简单。
举个例子,请注意当我们使用随机初始化的参数时,中间的矩阵 - 向量积突出的垂直模式 —— 这反映了一个事实:每个中间值都是左侧参数的列缩放的副本: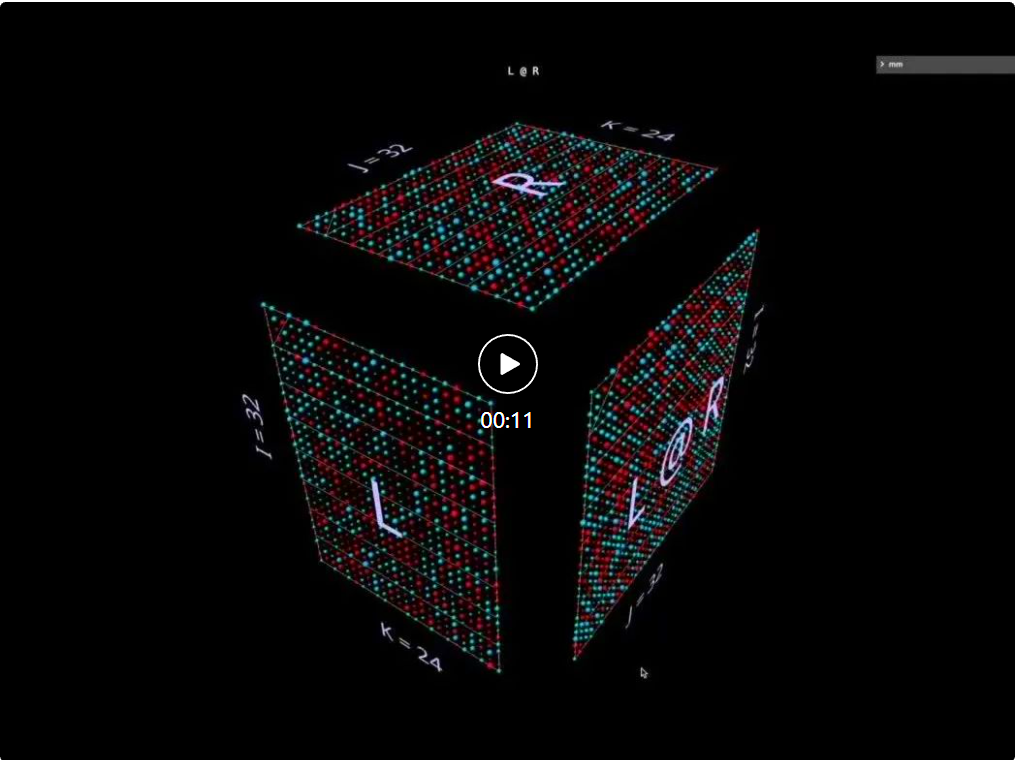
2c 向量 - 矩阵积
分解为向量 - 矩阵积的矩阵乘法看起来像一个水平平面,其在向下穿过立方体内部时将行绘制到结果上: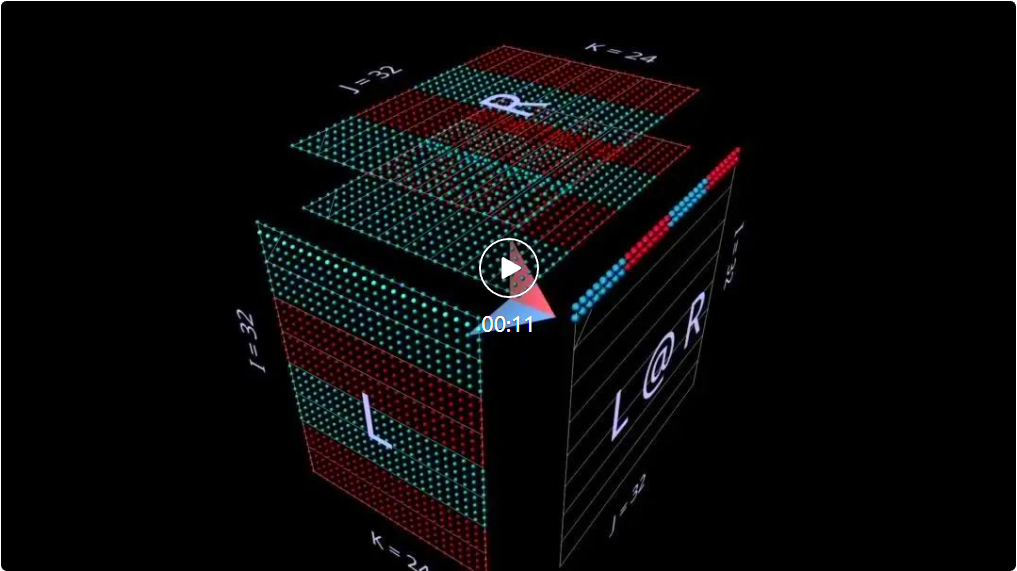
切换成随机初始化的参数,可以看到类似矩阵 - 向量积的模式 —— 只不过这次是水平模式,对应的事实是每个中间向量 - 矩阵积都是右侧参数的行缩放的副本。
在思考矩阵乘法如何表示其参数的秩和结构时,一种有用的做法是设想这两种模式在计算中同时发生: 这里还有另一个使用向量 - 矩阵积来构建直觉的示例,其中展示了单位矩阵的作用就像是一面呈 45 度角摆放的镜子,反射着其对应参数和结果:
这里还有另一个使用向量 - 矩阵积来构建直觉的示例,其中展示了单位矩阵的作用就像是一面呈 45 度角摆放的镜子,反射着其对应参数和结果: 
2d 对外积求和
第三次平面分解是沿着 k 轴,通过对向量外积逐点求和来计算矩阵乘法结果。这里我们可以看到外积平面「从后到前」扫过立方体,累积到结果中: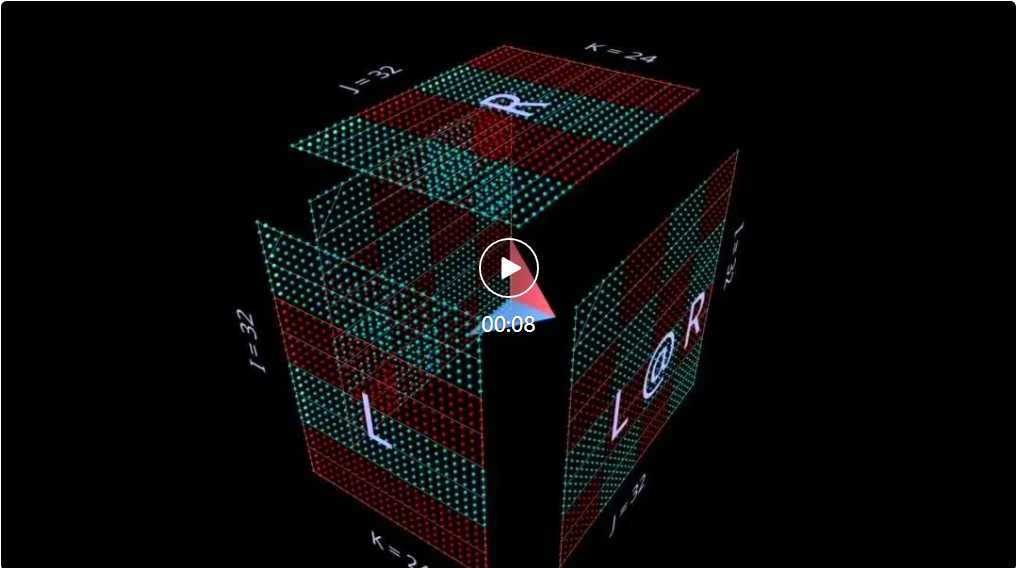
使用随机初始化的矩阵进行此分解,我们不仅可以看到值,还可以看到结果中的秩累积,因为每个秩为 1 的外积都被添加到其中。
这也从直觉上说明了为什么「低秩因式分解」(即通过构造参数在深度维度上较小的矩阵乘法来近似矩阵)在被近似的矩阵为低秩矩阵时的效果最好。这是后面会提到的 LoRA:
3 热身:表达式
我们可以怎样的方式将这种可视化方法扩展用于矩阵乘法的分解?之前的示例可视化的是矩阵 L 和 R 的单次矩阵乘法 L @ R,但要是 L 和 / 或 R 本身也是矩阵乘法呢?
事实证明这种方法可以很好地扩展用于复合表达式。关键规则很简单:子表达式(子)矩阵乘法是另一个立方体,其受到与父矩阵乘法一样的布局约束;子矩阵乘法的结果面同时也是父矩阵乘法对应的参数面,就像是共价共享的电子。
在这些约束限制中,我们可以按自己的需求排布子矩阵乘法的各个面。这里使用该工具的默认方案,这会生成交替的凸面和凹面立方体 —— 这种布局的实践效果很好,可以最大化地利用空间,同时尽可能减少遮挡。(但是布局是完全可定制的,详情访问 mm 工具页面。)
这一节将可视化机器学习模型的一些关键构建模块,以便读者熟悉这种视觉表示并从中获得新的直觉认识。
3a 左结合表达式
下面将会介绍两个 (A @ B) @ C 形式的表达式,每一个都有自己的独特形状和特征。(注意:mm 遵循矩阵乘法是左结合的约定,所以 (A @ B) @ C 可简单写为 A @ B @ C。)
首先为 A @ B @ C 赋予很有特点的 FFN 形状,其中「隐藏维度」比「输入」或「输出」维度宽。(具体来说,就此示例而言,这意味着 B 的宽度大于 A 或 C 的宽度。)
和单次矩阵乘法示例一样,浮动的箭头指向结果矩阵,其中蓝色箭羽来自左侧参数,红色箭羽来自右侧参数。

而当 B 的宽度小于 A 或 C 的宽度时,对 A @ B @ C 的可视化则会有一个瓶颈,类似自动编码器的形状。
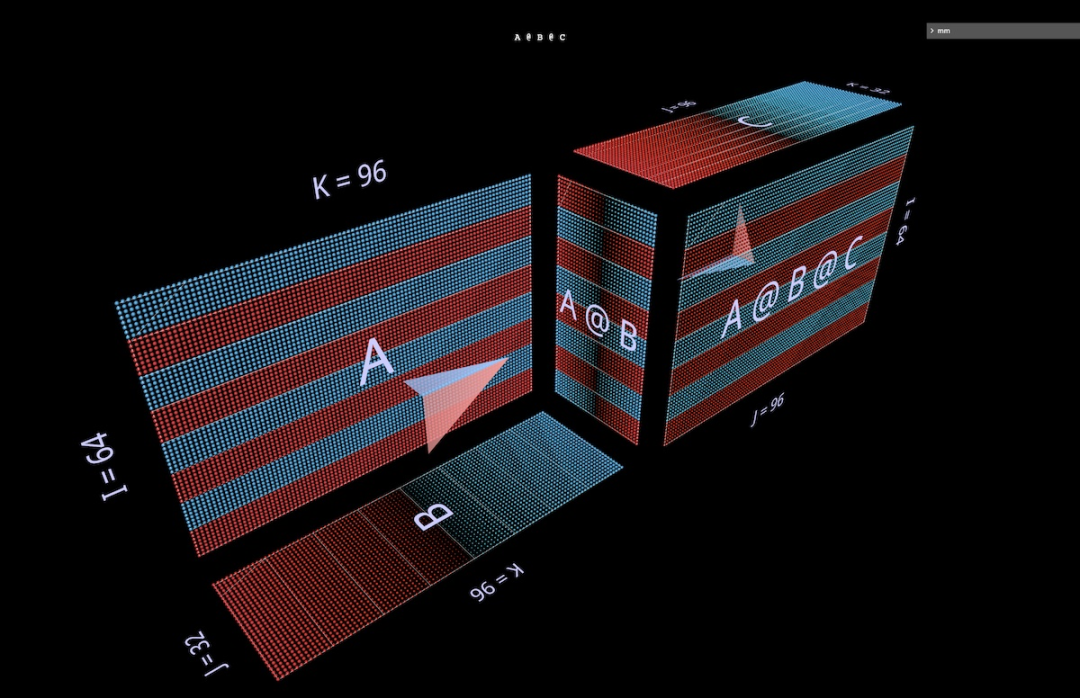
交替的凹凸模块的模式还可以扩展成任意长度的链:比如这个多层瓶颈:

3b 右结合表达式
接下来可视化右结合表达式 A @ (B @ C)。
与左结合表达式的水平扩展类似 —— 可以说是从根表达式的左侧参数发端,右结合表达式链是以垂直方式扩展,从根表达式的右侧参数发端。
人们有时候可以看到一个以右结合形式形成的 MLP,即右侧是柱状输入,权重层从右到左运行。使用上面描绘的二层 FFN 示例的矩阵(适当转置后),看起来会是这样,C 现在是输入,B 是第一层,A 是第二层:
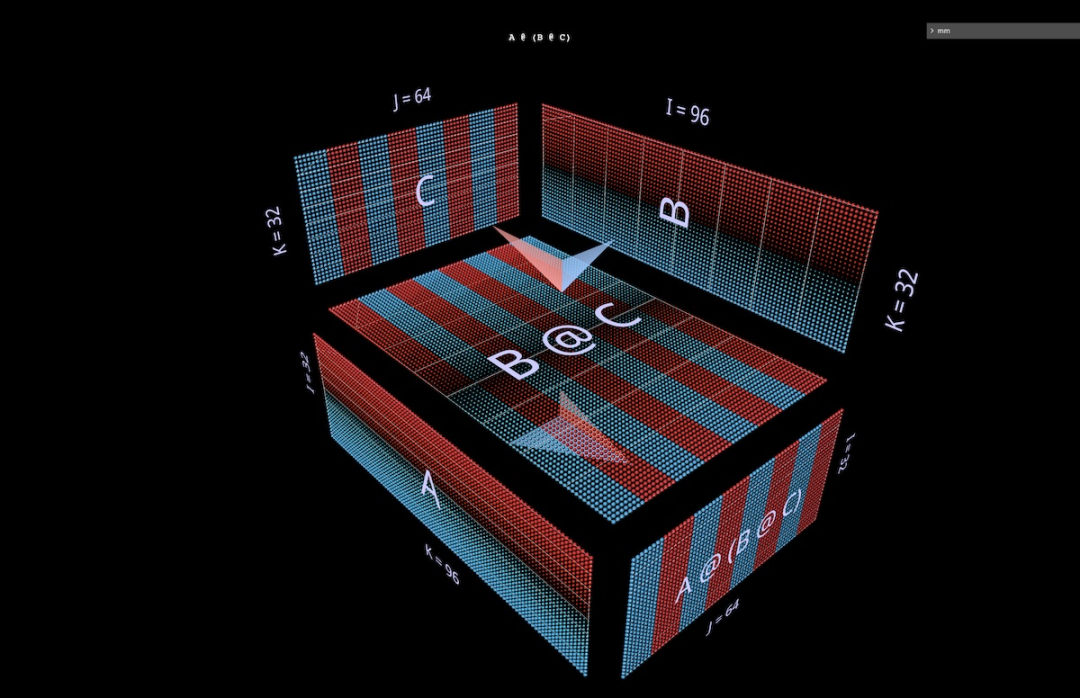
另外,除了箭羽的颜色(左侧为蓝色,右侧为红色),区分左右参数的第二个视觉提示是它们的方向:左侧参数的行与结果的行共面 —— 它们沿同一根轴 (i) 堆叠。比如上面的 (B @ C),这两个提示都能告诉我们 B 是左侧参数。
3c 二元表达式
对于可视化工具,要有用,就不能只用于简单的教学式示例,也要能方便地用于更复杂的表达式。在真实世界用例中,一个关键性结构组件是二元表达式 —— 左侧和右侧都有子表达式的矩阵乘法。
这里可视化了此类表达式中形状最简单的一个 (A @ B) @ (C @ D):

3d 一点注解:分区和并行性
完整阐述该主题超出了本文的范围,但后面我们会在注意力头部分看到它的实际效用。但这里热个身,看两个简单示例,了解下这种可视化风格可以如何让对并行化复合表达式的推理非常直观 —— 只需通过简单的几何分区。
第一个示例是将典型的「数据并行」分区应用于上面的左结合多层瓶颈示例。我们沿 i 分区,对初始左侧参数(「批」)和所有中间结果(「激活」)进行分段,但不对后续参数(「权重」)分段 —— 这种几何结构使得表达式中的哪些参与者被分段以及哪些保持完整变得显而易见:

第二个示例如果没有清晰的几何支持,就很难直觉地理解:它展示了如何通过沿 j 轴对左侧子表达式分区、沿 i 轴对右侧子表达式分区以及沿 k 轴对父表达式进行分区来并行化一个二元表达式:

4 深入注意力头
现在来看看 GPT-2 的注意力头 —— 具体来说是来自 NanoGPT 的 5 层第 4 头的 「gpt2」(small) 配置(层数 = 12,头数 = 12,嵌入数 = 768),通过 HuggingFace 使用了来自 OpenAI 的权重。输入激活取自在含 256 个 token 的 OpenWebText 训练样本上一次前向通过。
这个特定的头并无任何特殊之处,选择它主要是因为其计算的是一个非常常见的注意力模式,并且它位于模型中部,其中激活已经变得结构化并显示出一些有趣的纹理。
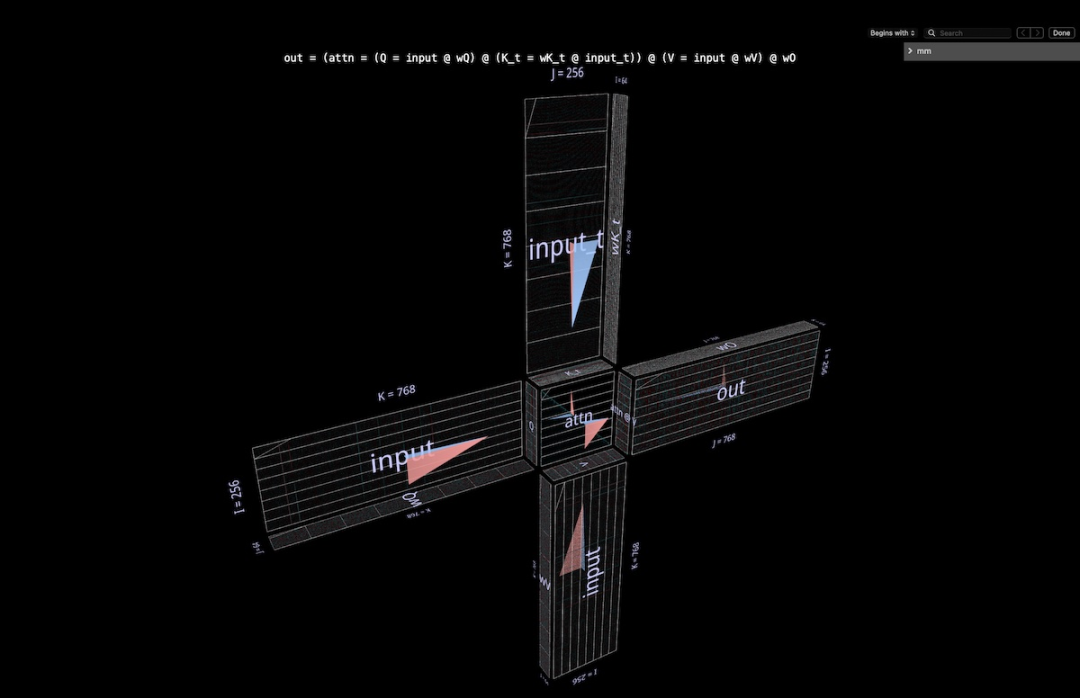
4a 结构
这个完整注意力头被可视化成了单个复合表达式,其始于输入,终于投影的输出。(注:为了保证自足性,这里按照 Megatron-LM 的描述对每个头执行输出投影。)
这一计算包含六次矩阵乘法:
Q = input @ wQ// 1K_t = wK_t @ input_t// 2V = input @ wV// 3attn = sdpa(Q @ K_t)// 4head_out = attn @ V // 5out = head_out @ wO // 6
简单描述一下这里在做什么:
风车的叶片为矩阵乘法 1、2、3 和 6:前一组是输入到 Q、K 和 V 的内投影;后者是从 attn @ V 回到嵌入维度的外投影。
中心有两个矩阵乘法;第一个计算的是注意力分数(后面的凸立方体),然后使用它们基于值向量得到输出 token(前面的凹立方体)。因果关系意味着注意力分数形成一个下三角形。
但读者最好能亲自详细探索这个工具,而不是只看截图或下面的视频,以便更详细地理解 —— 不管是其结构还是流过计算过程的实际值。
4b 计算和值
这里是注意力头的计算过程动画。具体来说,我们是看
sdpa (input @ wQ @ K_t) @ V @ wO
(即上面的矩阵乘法 1、4、5 和 6,其中 K_t 和 V 已经预先计算)是作为向量 - 矩阵积的融合链来计算:序列中的每一项都在一步之内从输入穿过注意力到输出。后面关于并行化的部分会提到更多有关这个动画的选择,但我们先看看计算的值能告诉我们什么。
我们可以看到很多有趣的东西:
在讨论注意力计算之前,可以看到低秩 Q 和 K_t 的形态是多么惊人。放大 Q @ K_t 向量 - 矩阵积动画,看起来会更加生动:Q 和 K 中大量通道(嵌入位置)在序列中看起来或多或少是恒定的,这意味着有用的注意力信号可能仅由一小部分嵌入驱动。理解和利用这种现象是 SysML ATOM transformer 效率项目的一部分。
也许人们最熟悉的是注意力矩阵中出现的强大但不完美的对角线。这是一种常见模式,出现在该模型(以及许多 Transformer)的许多注意力头中。它能产生局部注意力:紧邻输出 token 位置之前的小邻域中的值 token 很大程度上决定了输出 token 的内容模式。
然而,这个邻域的大小和其中各个 token 的影响变化很大 —— 这可以在注意力网格中的非对角 frost 中看到,也能在注意力矩阵沿序列下降时 attn [i] @ V 向量 - 矩阵积平面的波动模式中看到。
但请注意,局部邻域并不是唯一值得注意的东西:注意力网格的最左列(对应于序列的第一个 token )完全填充了非零(但波动)的值,这意味着每个输出 token 都会受到第一个值 token 一定程度的影响。
此外,当前 token 邻域和初始 token 之间的注意力分数主导性存在不精确但可辨别的振荡。该振荡的周期各有不同,但一般来说,一开始很短,然后沿序列向下移动而变长(类似地,在给定因果关系的情况下,与每一行的候选注意力 token 的数量相关)。
为了了解 (attn @ V) 的形成方式,不单独关注注意力是很重要的 ——V 也同等重要。每个输出项都是整个 V 向量的加权平均值:在注意力是完美对角线的极端情况下,attn @ V 只是 V 的精确副本。这里我们看到更有纹理的东西:可见的带状结构,其中特定 token 在注意力行的连续子序列上的得分很高,叠加在与 V 明显相似的矩阵上,但由于对角线较粗而有一些垂直遮挡。(旁注:根据 mm 参考指南,长按或按住 Control 键单击将显示可视化元素的实际数值。)
请记住,由于我们位于中间层(5 层),因此该注意力头的输入是一个中间表示,而不是原始 token 化文本。因此,在输入中看到的模式本身就发人深省 —— 特别是,强大的垂直线条是特定的嵌入位置,其值在序列的长段上统一具有高的幅度 —— 有时几乎是占满了。
但有趣的是,输入序列中的第一个向量是独特的,不仅打破了这些高幅度列的模式,而且几乎在每个位置都携带着非典型值(旁注:这里没有可视化,但这种模式反复出现在多个样本输入上)。
注意:关于最后两个要点,值得重申的是,这里可视化的是对单个样本输入的计算。在实践中,可以发现每个头都有一个特征模式,能在相当多的样本集合上一致(尽管不等同)地表达,但当查看任意包含激活的可视化时,需要记住:输入的完整分布可能会以微妙的方式影响它激发的想法和直觉。
最后,再次建议直接探索动画!
4c 注意力头有很多有趣的不同之处
继续之前,这里再通过一个演示展现简单地研究模型以了解其详细工作方式的有用性。
这是 GPT-2 的另一个注意力头。其行为模式与 5 层第 4 头大有不同 —— 这符合人们预期,毕竟它位于模型一个非常不同的部分。这个头位于第一层:0 层的第 2 头:

值得注意的点:
这个头的注意力分布很均匀。这会产生一个效果:将 V 的相对未加权的平均值(或者说 V 的合适的因果前缀)交到 attn @ V 的每一行;如动画所示:当我们向下移动注意力分数三角时,attn [i] @ V 向量 - 矩阵积有很小的波动,而不是简单的 V 的缩小比例的、逐渐揭示的副本。
attn @ V 具有惊人的垂直均匀性 —— 在嵌入的大柱状区域中,相同的值模式在整个序列中持续存在。人们可以将这些看作是每个 token 共享的属性。
旁注:一方面,考虑到注意力分布非常均匀的效果,人们可能会期望 attn @ V 具有一定的一致性。但是每一行都是由 V 的因果子序列而不是整个序列构成 —— 为什么这不会导致更多的变化,就像沿着序列向下移动时的渐进变形一样?通过视觉检查可知,V 沿其长度并不均匀,因此答案必定在于其值分布的一些更微妙的属性。
最后,在外投影后,这个头的输出在垂直方向上还要更加均匀。
我们能得到一个强烈的印象:该注意力头传递的大部分信息由序列中每个 token 共享的属性组成。其输出投影权重的构成能强化这种直觉。
总的来说,我们不由得会想:这个注意力头产生的极其规则、高度结构化的信息可能是通过稍微…… 不那么奢华的计算手段获得的。当然,这不是一个未经探索的领域,但可视化计算信号的明确性和丰富性对于产生新想法和推理现有想法都非常有用。
4d 重返介绍:免费的不变性
回头看,需要重申:我们之所以能够将注意力头等非平凡的复合操作可视化并让它们保持直观,是因为重要的代数性质(例如参数形状的限制方式或者哪些并行轴与哪些操作相交),这些性质不需要额外的思考:它们直接来自可视化对象的几何属性,而不是需要记住的额外规则。
举个例子,在这些注意力头可视化中,可以明显看出:
Q 和 attn @ V 的长度一样,K 和 V 的长度一样,这些配对的长度都彼此独立;
Q 和 K 的宽度一样,V 和 attn @ V 的宽度一样,这些配对的宽度都彼此独立。
这些结构在构造上就是真实的,就是结构组分位于复合结构的哪个部分以及它们的方向如何的简单结果。
这种「免费性质」的优势在探索典型结构的变体时特别有用 —— 一个明显的例子是一次解码一个自回归 token 中的单行高的注意力矩阵:

5 并行化注意力
上面 5 层第 4 头的动画可视化了注意力头中 6 个矩阵乘法中的 4 个。
它们被可视化为了一条向量 - 矩阵积的融合链,从而证实了一个几何直觉:从输入到输出的整个左结合链沿共享 i 轴呈层状,且可并行化。
5a 示例:沿 i 分区
为了在实践中并行计算,我们可将输入沿 i 轴划分为块。我们可以在该工具中可视化这种分区,通过指定将给定轴划分为特定数量的块 —— 在这些示例中将使用 8,但该数字并无特别之处。
除此之外,这种可视化清楚地表明,每次并行计算都需要完整的 wQ(用于内投影)、K_t 和 V(用于注意力)和 wO(用于外投影),因为它们沿这些矩阵的未分区维度与已分区矩阵相邻接:

5b 示例:双重分区
这里也给出沿多个轴进行分区的示例。为此,这里选择可视化该领域一个近期的创新成果,即 Block Parallel Transformer(BPT),其基于 Flash Attention 等一些研究成果,参阅论文:https://arxiv.org/pdf/2305.19370.pdf
首先,BPT 如上所述沿 i 进行分区 —— 并且实际上也将序列的这种水平分区一直延伸到注意力层的另一半边(FFN)。(对此的可视化将在后面展现。)
为了完全解决这个上下文长度问题,向 MHA 添加第二个分区 —— 注意力计算本身的分区(即沿 Q @ K_t 的 j 轴的分区)。这两个分区一起可将注意力分成块构成的网格:

从这个可视化可以清楚看到:
这种双重分区能有效解决上下文长度问题,因为我们现在能以视觉划分注意力计算中每次出现的序列长度。
第二次分区的「范围」:根据几何结构可以明显看出,K 和 V 的内投影计算可与核心的双矩阵乘法一起分区。
注意一个微妙细节:这里的视觉暗示是我们还可以沿 k 并行化后续的矩阵乘法 attn @ V 并以 split-k 风格对部分结果求和,从而并行化整个双重矩阵乘法。但 sdpa () 中的逐行 softmax 增加了要求:在计算 attn @ V 的相应行之前,每一行都要将其所有分段归一化,这会在注意力计算和最终矩阵乘法之间添加一个额外的逐行步骤。
6 注意力层的大小
众所周知,注意力层的前一半(MHA)由于其二次复杂度而有很高的计算需求,但后一半(FFN)也有自己的需求,这要归因于其隐藏维度的宽度,其通常是模型嵌入维度的宽度的 4 倍。可视化完整注意力层的生物量有助于建立关于该层两半部分如何相互比较的直觉认识。
6a 可视化完整的注意力层
下面是一个完整的注意力层,前一半(MHA)位于后面,后一半(FFN)位于前面。同样,箭头指向计算的方向。
注:
该可视化描绘的不是单个注意力头,而是显示了未切片的 Q/K/V 权重和围绕中心双重矩阵乘法的投影。当然这没有将完整的 MHA 运算忠实地可视化出来 —— 但这里的目标是更清楚地了解该层的两半中的相对矩阵大小,而不是每半执行的相对计算量。(此外,这里的权重使用了随机值而非真实权重。)
这里使用的维度有所收缩以保证浏览器(相对)能带得动,但比例保持一样(来自 NanoGPT 的 small 配置):模型嵌入维度 = 192(原本是 768)、FFN 嵌入维度 = 768(原本是 3072)、序列长度 = 256(原本是 1024),尽管序列长度对模型没有根本性影响。(从视觉上看,序列长度的变化将表现为输入叶片宽度的变化,从而导致注意力中心大小和下游垂直平面高度的变化。)

6b 可视化 BPT 分区层
简单地回顾一下 Blockwise Parallel Transformer,这里是在整个注意力层的语境中可视化 BPT 的并行化方案(和上面一样省略了各个头)。特别要注意,沿 i(序列块)的分区以怎样的方式扩展通过 MHA 和 FFN 两半边:

6c 对 FFN 进行分区
这种可视化方法建议进行额外的分区,该分区与上面描述的分区正交 —— 在注意力层的 FFN 半边,将双重矩阵乘法 (attn_out @ FFN_1) @ FFN_2 分开,首先沿 j 进行 attn_out @ FFN_1,然后沿 k 与 FFN_2 执行后续的矩阵乘法。这种分区会对两个 FFN 权重层进行切片,以减少计算中每个参与组分的容量要求,但代价是部分结果的最终求和。
下面是将这种分区方法应用于未分区的注意力层的样子:

下面则是应用于以 BPT 方式分区的层的情况:

6d 可视化一次一个 token 解码的过程
在自回归式的一次一个 token 的解码过程中,查询向量由单个 token 构成。你可以在头脑中想象一下这种情况下的注意力层会是什么样子,这很有启发性 —— 单个嵌入行穿过一个巨大的平铺的权重平面。
除了强调与激活相比权重的巨大性之外,这种观点还能让人想起这样一个概念:K_t 和 V 的功能类似于一个 6 层 MLP 中动态生成的层,尽管 MHA 本身的 mux/demux 计算会使这种对应关系不精确:

7 LoRA
近期的 LoRA 论文《LoRA: Low-Rank Adaptation of Large Language Models》描述了一种高效的微调技术,该技术基于这一思想:微调期间引入的权重 δ 是低秩的。根据这篇论文,这「允许我们通过在适应过程中优化密集层变化的秩分解矩阵来间接地训练神经网络中的一些密集层…… 同时保持预训练权重处于冻结状态。」
7a 基本思想
简而言之,关键一步是训练权重矩阵的因子而不是矩阵本身:用一个 I x K 张量和 K x J 张量的矩阵乘法来替代 I x J 权重张量,其中要保证 K 为一个较小值。
如果 K 足够小,则尺寸方面可能会有很大赢面,但也有权衡之处:降低 K 也会降低积可以表达的秩。这里通过一个示例说明尺寸上的节省与对结果的结构化影响,这里是随机的 128 x 4 左侧参数和 4 x 128 右侧参数的矩阵乘法 —— 即一个 128 x 128 矩阵的秩为 4 的分解。注意 L @ R 中的垂直和水平模式:

7b 将 LoRA 应用于注意力头
LoRA 将这种分解方法应用于微调过程的方式是:
为每个权重张量创建一个要进行微调的低秩分解,并训练其因子,同时保持原始权重冻结;
微调之后,将每对低秩因子相乘,得到一个原始权重张量形状的矩阵,并将其添加到原始的预训练权重张量中。
下面的可视化显示了一个注意力头,其权重张量 wQ、wK_t、wV、wO 被低秩分解 wQ_A @ wQ_B 等替换。从视觉上看,因子矩阵呈现为沿风车叶片边缘的低栅栏:
以上是以3D视角洞悉矩阵乘法,这就是AI思考的样子的详细内容。更多信息请关注PHP中文网其他相关文章!

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

热门话题
 DeepMind机器人打乒乓球,正手、反手溜到飞起,全胜人类初学者
Aug 09, 2024 pm 04:01 PM
DeepMind机器人打乒乓球,正手、反手溜到飞起,全胜人类初学者
Aug 09, 2024 pm 04:01 PM
但可能打不过公园里的老大爷?巴黎奥运会正在如火如荼地进行中,乒乓球项目备受关注。与此同时,机器人打乒乓球也取得了新突破。刚刚,DeepMind提出了第一个在竞技乒乓球比赛中达到人类业余选手水平的学习型机器人智能体。论文地址:https://arxiv.org/pdf/2408.03906DeepMind这个机器人打乒乓球什么水平呢?大概和人类业余选手不相上下:正手反手都会:对手采用多种打法,该机器人也能招架得住:接不同旋转的发球:不过,比赛激烈程度似乎不如公园老大爷对战。对机器人来说,乒乓球运动
 首配机械爪!元萝卜亮相2024世界机器人大会,发布首个走进家庭的国际象棋机器人
Aug 21, 2024 pm 07:33 PM
首配机械爪!元萝卜亮相2024世界机器人大会,发布首个走进家庭的国际象棋机器人
Aug 21, 2024 pm 07:33 PM
8月21日,2024世界机器人大会在北京隆重召开。商汤科技旗下家用机器人品牌“元萝卜SenseRobot”家族全系产品集体亮相,并最新发布元萝卜AI下棋机器人——国际象棋专业版(以下简称“元萝卜国象机器人”),成为全球首个走进家庭的国际象棋机器人。作为元萝卜的第三款下棋机器人产品,全新的国象机器人在AI和工程机械方面进行了大量专项技术升级和创新,首次在家用机器人上实现了通过机械爪拾取立体棋子,并进行人机对弈、人人对弈、记谱复盘等功能,
 Claude也变懒了!网友:学会给自己放假了
Sep 02, 2024 pm 01:56 PM
Claude也变懒了!网友:学会给自己放假了
Sep 02, 2024 pm 01:56 PM
开学将至,该收心的不止有即将开启新学期的同学,可能还有AI大模型。前段时间,Reddit上挤满了吐槽Claude越来越懒的网友。「它的水平下降了很多,经常停顿,甚至输出也变得很短。在发布的第一周,它可以一次性翻译整整4页文稿,现在连半页都输出不了了!」https://www.reddit.com/r/ClaudeAI/comments/1by8rw8/something_just_feels_wrong_with_claude_in_the/在一个名为「对Claude彻底失望了的帖子里」,满满地
 世界机器人大会上,这家承载「未来养老希望」的国产机器人被包围了
Aug 22, 2024 pm 10:35 PM
世界机器人大会上,这家承载「未来养老希望」的国产机器人被包围了
Aug 22, 2024 pm 10:35 PM
正在北京举行的世界机器人大会上,人形机器人的展示成为了现场绝对的焦点,在星尘智能的展台上,由于AI机器人助理S1在一个展区上演扬琴、武术、书法三台大戏,能文能武,吸引了大量专业观众和媒体的驻足。在带弹性的琴弦上的优雅演奏,让S1展现出速度、力度、精度兼具的精细操作和绝对掌控。央视新闻对「书法」背后的模仿学习和智能控制进行了专题报道,公司创始人来杰解释到,丝滑动作的背后,是硬件侧追求最好力控和最仿人身体指标(速度、负载等),而是在AI侧则采集人的真实动作数据,让机器人遇强则强,快速学习进化。而敏捷
 ACL 2024奖项公布:华科大破译甲骨文最佳论文之一、GloVe时间检验奖
Aug 15, 2024 pm 04:37 PM
ACL 2024奖项公布:华科大破译甲骨文最佳论文之一、GloVe时间检验奖
Aug 15, 2024 pm 04:37 PM
本届ACL大会,投稿者「收获满满」。为期六天的ACL2024正在泰国曼谷举办。ACL是计算语言学和自然语言处理领域的顶级国际会议,由国际计算语言学协会组织,每年举办一次。一直以来,ACL在NLP领域的学术影响力都位列第一,它也是CCF-A类推荐会议。今年的ACL大会已是第62届,接收了400余篇NLP领域的前沿工作。昨天下午,大会公布了最佳论文等奖项。此次,最佳论文奖7篇(两篇未公开)、最佳主题论文奖1篇、杰出论文奖35篇。大会还评出了资源论文奖(ResourceAward)3篇、社会影响力奖(
 鸿蒙智行享界S9及全场景新品发布会,多款重磅新品齐发
Aug 08, 2024 am 07:02 AM
鸿蒙智行享界S9及全场景新品发布会,多款重磅新品齐发
Aug 08, 2024 am 07:02 AM
今天下午,鸿蒙智行正式迎来了新品牌与新车。 8月6日,华为举行鸿蒙智行享界S9及华为全场景新品发布会,带来了全景智慧旗舰轿车享界S9、问界新M7Pro和华为novaFlip、MatePadPro12.2英寸、全新MatePadAir、华为毕升激光打印机X1系列、FreeBuds6i、WATCHFIT3和智慧屏S5Pro等多款全场景智慧新品,从智慧出行、智慧办公到智能穿戴,华为全场景智慧生态持续构建,为消费者带来万物互联的智慧体验。鸿蒙智行:深度赋能,推动智能汽车产业升级华为联合中国汽车产业伙伴,为
 李飞飞团队提出ReKep,让机器人具备空间智能,还能整合GPT-4o
Sep 03, 2024 pm 05:18 PM
李飞飞团队提出ReKep,让机器人具备空间智能,还能整合GPT-4o
Sep 03, 2024 pm 05:18 PM
视觉与机器人学习的深度融合。当两只机器手丝滑地互相合作叠衣服、倒茶、将鞋子打包时,加上最近老上头条的1X人形机器人NEO,你可能会产生一种感觉:我们似乎开始进入机器人时代了。事实上,这些丝滑动作正是先进机器人技术+精妙框架设计+多模态大模型的产物。我们知道,有用的机器人往往需要与环境进行复杂精妙的交互,而环境则可被表示成空间域和时间域上的约束。举个例子,如果要让机器人倒茶,那么机器人首先需要抓住茶壶手柄并使之保持直立,不泼洒出茶水,然后平稳移动,一直到让壶口与杯口对齐,之后以一定角度倾斜茶壶。这
 分布式人工智能盛会DAI 2024征稿:Agent Day,强化学习之父Richard Sutton将出席!颜水成、Sergey Levine以及DeepMind科学家将做主旨报告
Aug 22, 2024 pm 08:02 PM
分布式人工智能盛会DAI 2024征稿:Agent Day,强化学习之父Richard Sutton将出席!颜水成、Sergey Levine以及DeepMind科学家将做主旨报告
Aug 22, 2024 pm 08:02 PM
会议简介随着科技的飞速发展,人工智能已经成为了推动社会进步的重要力量。在这个时代,我们有幸见证并参与到分布式人工智能(DistributedArtificialIntelligence,DAI)的创新与应用中。分布式人工智能是人工智能领域的重要分支,这几年引起了越来越多的关注。基于大型语言模型(LLM)的智能体(Agent)异军突起,通过结合大模型的强大语言理解和生成能力,展现出了在自然语言交互、知识推理、任务规划等方面的巨大潜力。AIAgent正在接棒大语言模型,成为当前AI圈的热点话题。Au






