利润预测不再困难,scikit-learn线性回归法让你事半功倍
1、简介
生成式人工智能无疑是一个改变游戏规则的技术,但对于大多数商业问题来说,回归和分类等传统的机器学习模型仍然是首选。
重写后的内容:设想一下私募股权或风险投资等投资者如何利用机器学习。要回答这个问题,首先需要了解投资者关注的数据以及数据的使用方式。投资公司的决策不仅仅基于可量化的数据,例如支出、增长和烧钱率等,还包括创始人的记录、客户反馈和产品体验等定性数据
本文将介绍线性回归的基础知识,可以在这里找到完整的代码。
需要重写的内容是:【代码】:https://github.com/RoyiHD/linear-regression
2、项目设置
本文将使用Jupyter Notebook进行这个项目。首先导入一些库。
导入库
# 绘制图表import matplotlib.pyplot as plt# 数据管理和处理from pandas import DataFrame# 绘制热力图import seaborn as sns# 分析from sklearn.metrics import r2_score# 用于训练和测试的数据管理from sklearn.model_selection import train_test_split# 导入线性模型from sklearn.linear_model import LinearRegression# 代码注释from typing import List
3、数据
为了简化问题,本文将使用区域数据。这些数据代表了公司的支出类别和利润。可以看到一些不同数据点的示例。本文希望使用支出数据来训练一个线性回归模型并预测利润。
重要的是要理解本文所描述的数据是关于一家公司的支出情况。只有当将支出数据与收入增长、当地税收、摊销和市场状况等数据结合起来时,才能得出有意义的预测能力
R&D Spend |
行政管理 |
Marketing |
投资收益 |
需要进行重写的内容是:165349.2 |
136897.8 |
需要重写的内容是:471784.1 |
需要改写的内容是:192261.83 |
162597.7 |
需要被重写的内容是:151377.59 |
443898.53 |
191792.06 |
153441.51 |
101145.55 |
需要重新写作的内容是:407934.54 |
需要重写的是:191050.39 |
加载数据
companies: DataFrame = pd.read_csv("companies.csv", header = 0)4、数据可视化
了解数据对于确定要使用的特征、需要进行归一化和转换的特征、从数据中删除异常值以及对特定数据点进行的处理是很重要的。
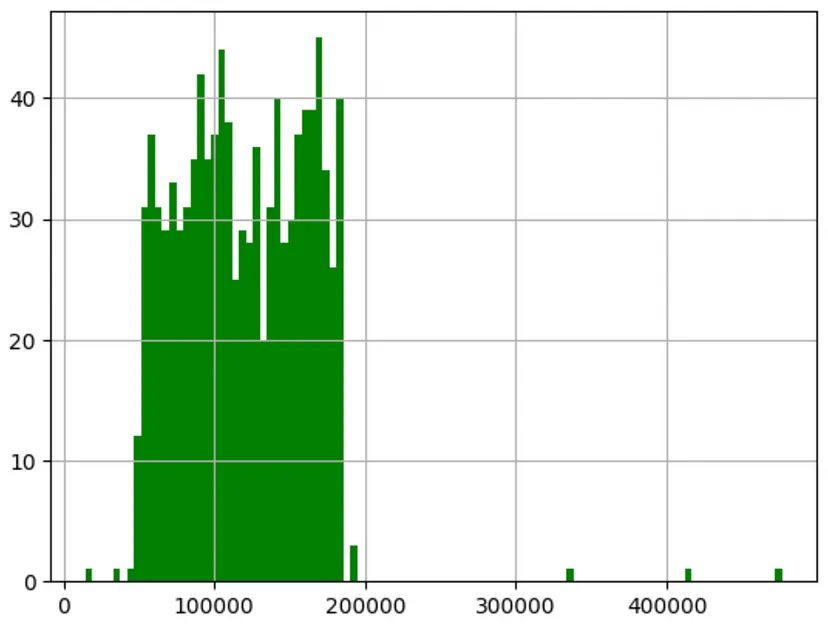
目标(利润)直方图
可以直接使用DataFrame绘制直方图(Pandas使用Matplotlib来绘制数据帧),可以直接访问利润并绘制它。
companies['Profit'].hist( color='g', bins=100);
 图片
图片
从数据中可以清楚地看出,利润超过20万美元的异常值非常罕见。这表明本文所涉及的数据代表的是规模较大的公司。鉴于异常值数量较少,可以将其保留
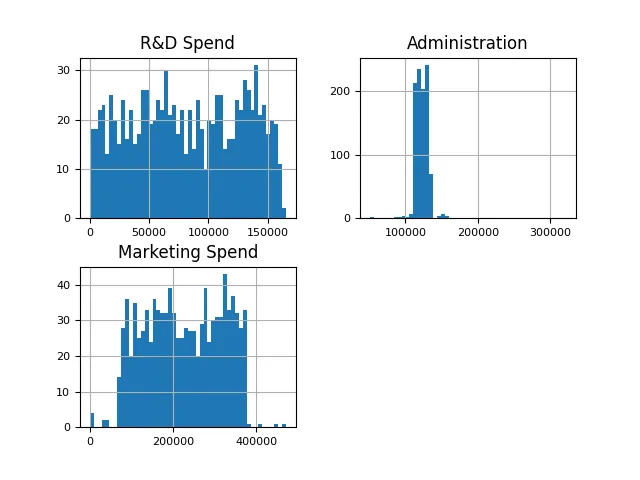
特征(支出)直方图
在这里,本文旨在使用特征的直方图,并观察其分布情况。Y轴表示数字频率,X轴表示支出
companies[["R&D Spend", "行政管理", "Marketing Spend"]].hist(figsize=(16, 20), bins=50, xlabelsize=8, ylabelsize=8)
 图片
图片
可以观察到一个健康的分布,只有很少的异常值。根据直觉,可以预期投入更多资金在研发和市场营销上的公司会获得更高的利润。从下面的散点图中可以看出,研发支出和利润之间存在明显的相关性
profits: DataFrame = companies[["Profit"]]research_and_development_spending: DataFrame = companies[["R&D Spend"]]figure, ax = plt.subplots(figsize = (9, 9))plt.xlabel("R&D Spending")plt.ylabel("Profits")ax.scatter(research_and_development_spending, profits, s=60, alpha=0.7, edgecolors="k",color='g',linewidths=0.5)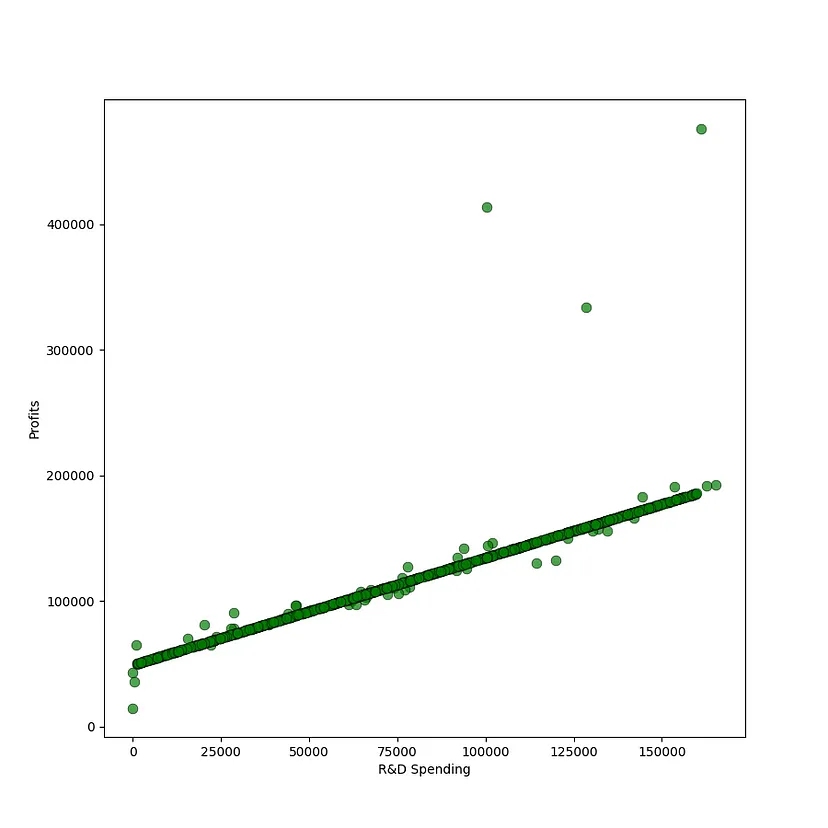 图片
图片
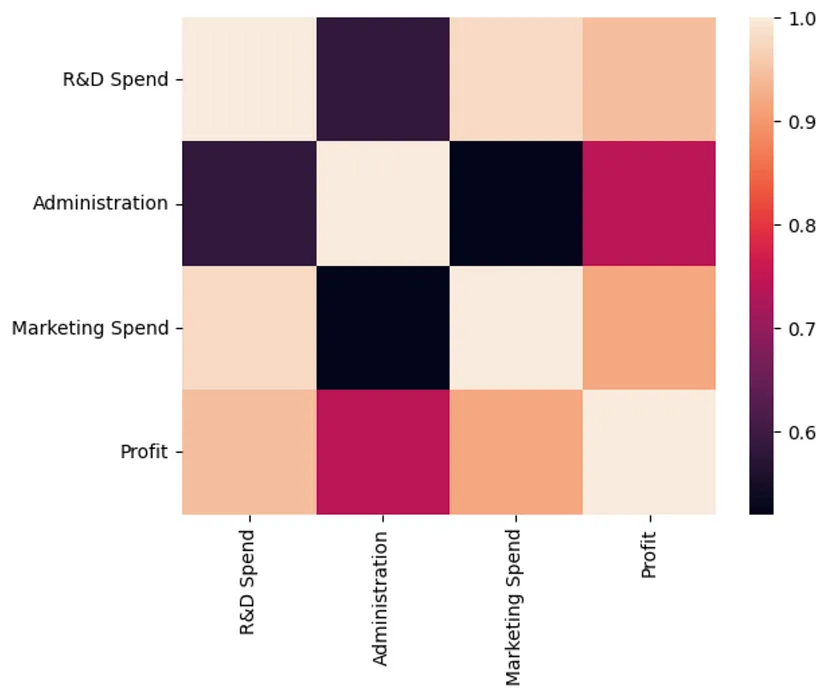
可以使用相关的热图来进一步探索支出和利润之间的关系。从图中可以观察到研发和市场营销支出与利润之间的相关性比行政支出更高
sns.heatmap(companies.corr())
 图片
图片
5、模型训练
首先需要将数据集分割为训练集和测试集两部分。Sklearn提供了一个辅助方法来完成这个任务。鉴于本文的数据集很简单且足够小,可以按照以下方式将特征和目标分离开来。
数据集
features: DataFrame = companies[["R&D Spend", "行政管理", "Marketing Spend",]]targets: DataFrame = companies[["Profit"]]train_features, test_features, train_targets, test_targets = train_test_split(features, targets,test_size=0.2)
大多数数据科学家会使用不同的命名约定,如X_train、y_train或其他类似的变体。
模型训练
现在可以创建并训练模型了。Sklearn使事情变得非常简单。
model: LinearRegression = LinearRegression()model.fit(train_features, train_targets)
6、模型评估
本文希望对模型的性能及其可用性进行评估。首先查看一下计算得到的系数。在机器学习中,系数是用来与每个特征相乘的学习到的权重或数值。期望看到每个特征都有一个学习系数。
coefficients = model.coef_"""We should see the following in our consoleCoefficients[[0.55664299 1.08398919 0.07529883]]"""
正如上述所看到的,有3个系数,每个特征对应一个系数(“研发支出”、“行政支出”、“市场营销支出”)。还可以将其绘制成图表,以便更直观地了解每个系数。
plt.figure()plt.barh(train_features.columns, coefficients[0])plt.show()
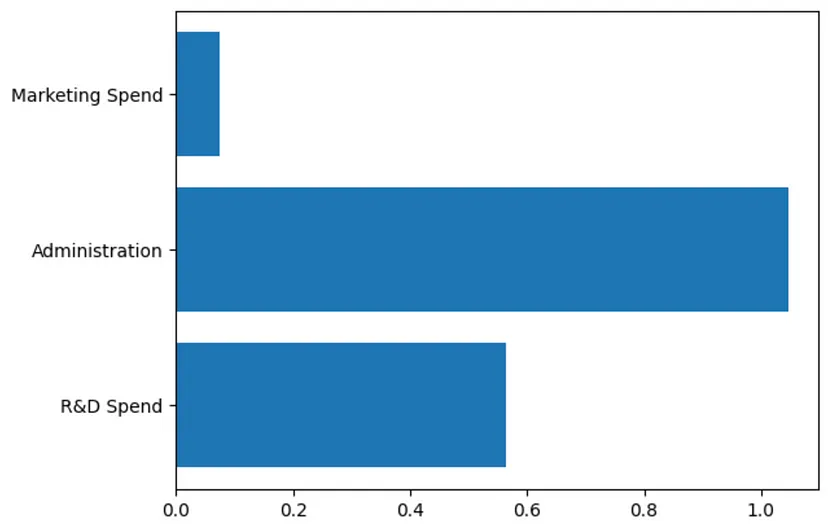 图片
图片
计算误差
希望了解模型的误差率,我们将使用Sklearn的R2得分
test_predictions: List[float] = model.predict(test_features)root_squared_error: float = r2_score(test_targets, test_predictions)"""floatWe should see an ouput similar to this0.9781424529214315"""
离1越近,模型就越准确。实际上可以用一种非常简单的方式对这一点进行测试。
使用下面的支出模型来预测利润,并希望得到一个接近192261美元的数字,可以提取数据集的第一行
"R&D Spend" |"行政管理" |"Marketing Spend" | "Profit"需要进行重写的内容是:165349.2 136897.8需要重写的内容是:471784.1需要改写的内容是:192261.83
接下来创建一个推理请求。
inference_request: DataFrame = pd.DataFrame([{"R&D Spend":需要进行重写的内容是:165349.2, "行政管理":136897.8, "Marketing Spend":需要重写的内容是:471784.1 }])运行模型。
inference: float = model.predict(inference_request)"""We should get a number that is around199739.88721901"""
现在可以看到的误差率是abs(199739-192261)/192261=0.0388。这是非常准确的。
7、结论
处理数据、搭建模型和分析数据有很多方法。没有一种解决方案适用于所有情况,当用机器学习解决业务问题时,其中一个关键过程是搭建多个旨在解决同一个问题的模型,并选择最有前途的模型
以上是利润预测不再困难,scikit-learn线性回归法让你事半功倍的详细内容。更多信息请关注PHP中文网其他相关文章!

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

热门话题
 我尝试了使用光标AI编码的Vibe编码,这太神奇了!
Mar 20, 2025 pm 03:34 PM
我尝试了使用光标AI编码的Vibe编码,这太神奇了!
Mar 20, 2025 pm 03:34 PM
Vibe编码通过让我们使用自然语言而不是无尽的代码行创建应用程序来重塑软件开发的世界。受Andrej Karpathy等有远见的人的启发,这种创新的方法使Dev
 2025年2月的Genai推出前5名:GPT-4.5,Grok-3等!
Mar 22, 2025 am 10:58 AM
2025年2月的Genai推出前5名:GPT-4.5,Grok-3等!
Mar 22, 2025 am 10:58 AM
2025年2月,Generative AI又是一个改变游戏规则的月份,为我们带来了一些最令人期待的模型升级和开创性的新功能。从Xai的Grok 3和Anthropic的Claude 3.7十四行诗到Openai的G
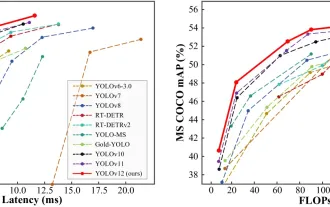 如何使用Yolo V12进行对象检测?
Mar 22, 2025 am 11:07 AM
如何使用Yolo V12进行对象检测?
Mar 22, 2025 am 11:07 AM
Yolo(您只看一次)一直是领先的实时对象检测框架,每次迭代都在以前的版本上改善。最新版本Yolo V12引入了进步,可显着提高准确性
 最佳AI艺术生成器(免费付款)创意项目
Apr 02, 2025 pm 06:10 PM
最佳AI艺术生成器(免费付款)创意项目
Apr 02, 2025 pm 06:10 PM
本文回顾了AI最高的艺术生成器,讨论了他们的功能,对创意项目的适用性和价值。它重点介绍了Midjourney是专业人士的最佳价值,并建议使用Dall-E 2进行高质量的可定制艺术。
 Chatgpt 4 o可用吗?
Mar 28, 2025 pm 05:29 PM
Chatgpt 4 o可用吗?
Mar 28, 2025 pm 05:29 PM
Chatgpt 4当前可用并广泛使用,与诸如ChatGpt 3.5(例如ChatGpt 3.5)相比,在理解上下文和产生连贯的响应方面取得了重大改进。未来的发展可能包括更多个性化的间
 最佳AI聊天机器人比较(Chatgpt,Gemini,Claude&更多)
Apr 02, 2025 pm 06:09 PM
最佳AI聊天机器人比较(Chatgpt,Gemini,Claude&更多)
Apr 02, 2025 pm 06:09 PM
本文比较了诸如Chatgpt,Gemini和Claude之类的顶级AI聊天机器人,重点介绍了其独特功能,自定义选项以及自然语言处理和可靠性的性能。
 如何将Mistral OCR用于下一个抹布模型
Mar 21, 2025 am 11:11 AM
如何将Mistral OCR用于下一个抹布模型
Mar 21, 2025 am 11:11 AM
MISTRAL OCR:通过多模式文档理解彻底改变检索效果 检索增强的生成(RAG)系统具有明显高级的AI功能,从而可以访问大量的数据存储,以获得更明智的响应
 顶级AI写作助理来增强您的内容创建
Apr 02, 2025 pm 06:11 PM
顶级AI写作助理来增强您的内容创建
Apr 02, 2025 pm 06:11 PM
文章讨论了Grammarly,Jasper,Copy.ai,Writesonic和Rytr等AI最高的写作助手,重点介绍了其独特的内容创建功能。它认为Jasper在SEO优化方面表现出色,而AI工具有助于保持音调的组成






