首个支持4-bit浮点量化的LLM来了，解决LLaMA、BERT等的部署难题

大语言模型 (LLM) 压缩一直备受关注，后训练量化（Post-training Quantization) 是其中一种常用算法，但是现有 PTQ 方法大多数都是 integer 量化，且当比特数低于 8 时，量化后模型的准确率会下降非常多。想较于 Integer (INT) 量化，Floating Point (FP) 量化能更好的表示长尾分布，因而越来越多的硬件平台开始支持 FP 量化。而这篇文章给出了大模型 FP 量化的解决方案。文章发表在 EMNLP 2023 上。

• 论文地址：https://arxiv.org/abs/2310.16836
• 代码地址：https://github.com/nbasyl/LLM-FP4

要了解本文，必须要先具备基本的有关 Floating Point Format 以及 Floating Point Quantization 的知识，首先 Floating Point Number 可以用以下公式表示:

s 代表正负符号位 (sign bit)，m 代表尾数位 (mantissa bits)，e 代表指数位 (exponent bits)。p 是一个介于 0 到 2^e - 1 之间的值，用来表示当前数字该被划分到哪一个指数区间，d 取 0 或 1 的值，用来表示第 i 个 mantissa bit。b 是 bias，一个用来调整 exponent 区间的整数值。

在接下来的部分中，我们将介绍浮点数量化是如何工作的。首先，输入值必须经过一个称为“scale and clip”的步骤。这个步骤首先将输入值裁剪到浮点数能够表示的最大范围（±Qmax），具体计算公式如下：

可以看到类似于 integer 量化，FP 量化也会加入一个 full-precision 的缩放因子 (scaling factor) 来缩放 input 到合适的区间。而缩放因子在运算矩阵乘法的时候，和低比特的矩阵乘法分开计算，所以并不会造成很大的 overhead。融入了这个 full-precision 的缩放因子之后，不同的 quantized tensor 能够被相应地 clip 到不同的最大最小值区间。在实际使用过程中，会根据输入 tensor 的值域确定需要的量化区间，然后利用公式 (4) 推导出相对应的 bias。注意公式 (4) 里的 bias 可以被用作实数值的缩放因子，见公式 (2)(3)。

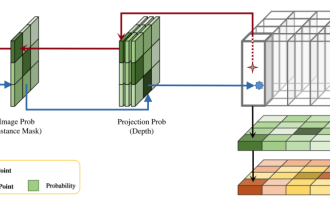
浮点数量化的下一个步骤是将决定好的量化区间内的值分配到相应的量化区间中，这个过程被称为比较和量化：

上图直观说明了量化的过程，当前的输入值，在用公式 5 比较过后，量化到不同的量化区间中。

在得到量化过的 activation 和 weight 后，这里的 scaling factor 提到前面先计算，而达到如下的 efficient matrix multiplication，完成矩阵乘法的加速：

接着本文指出 FP 量化的准确度，和 exponent bits 的设定以及量化的区间息息相关。

在之前的论文中，已经验证了不同的FP格式（即浮点数的指数位/尾数位设定）之间存在巨大的量化误差差异。只有当选择合适的FP格式时，FP量化能够比INT量化更好地表示长尾分布

这篇文章提出了一个解决方案，即采用基于搜索的浮点量化算法，以综合搜索的方式确定最适合的浮点数的指数位和尾数位设定以及相应的量化区间

除此之外，在各种不同类别的Transformer模型（Bert, LLaMA, ViT）中，还存在一个现象严重影响量化的难度：即模型的激活中不同通道之间的数量级差异很大，而同一通道之间的数量级非常一致。之前的研究LLM.int8和SmoothQuant也发现了类似的现象，但本文指出这个现象不仅存在于LLM中，其他Transformer模型（如下所示，LLaMA、BERT和DeIT-S）的激活分布也发现了类似的现象：

从图中可以看到，那些异常大的 channel 都比剩余的 channel 大很多，所以在量化 activation tensor 的过程中，量化的精度很大程度会被这些异常值决定，从而抑制其他 channel 值的量化区间，最终降低整体影响量化精度。这会导致量化的最终结果崩坏，尤其当比特数降到一定程度的时候。值得注意的是，只有 tensor-wise 和 token-wise 量化可以在 efficient matrix multipilication 的时候将 scaling factor 提取出来，而 channel-wise 量化是不支持 efficient matrix multipilication 的，见下图。

为了同时解决问题并保持高效率的矩阵乘法，本文使用少量的校正数据集来预先计算激活每个通道的最大值，并计算缩放因子。然后将缩放因子拆分为一个针对每个张量的实数乘以每个通道的2的幂。这个2的幂可以用FP中的指数偏差表示。整个过程可以通过以下公式表示：

进一步地，在 calibration 完成之后，这个 per-channel exponent bias 就不再变化，因此可以和 weight quantization 一起进行预计算 (pre-compute)，将这个 per-channel exponent bias 整合进量化后的 weights 中，提高量化精度。完整的过程如以下公式：

在预偏移之后，可以观察到原本激活函数中的每个通道的全精度偏置的位置变成了一个基于张量的实数缩放因子，同时将被分解的整数偏置移到了权重中原本整数偏置的位置，具体见公式4

从而这个方法 (pre-shifted exponent bias) 能在维持 efficient matrix multiplication 的原则下，更好得提高量化精度，方法的直观展示如下图所示：

最后本文展示 Floating Point Quantization (FPQ) 方法，在 LLaMA, BERT 以及 ViTs 模型上，4-bit 量化皆取得了远超 SOTA 的结果。特别是，这篇文章展示了 4-bit 量化的 LLaMA-13B 模型，在零样本推理任务上达到平均 63.1 的分数，只比完整精度模型低了 5.8 分，且比之前的 SOTA 方法平滑量高出了 12.7，这是目前少数已知可行的 4-bit 量化方案了。

以上是首个支持4-bit浮点量化的LLM来了，解决LLaMA、BERT等的部署难题的详细内容。更多信息请关注PHP中文网其他相关文章！