11个基本分布,数据科学家95%的时间都在使用
继上次盘点《数据科学家95%的时间都在使用的11个基本图表》之后,今天将为大家带来数据科学家95%的时间都在使用的11个基本分布。掌握这些分布,有助于我们更深入地理解数据的本质,并在数据分析和决策过程中做出更准确的推断和预测。

1. 正态分布
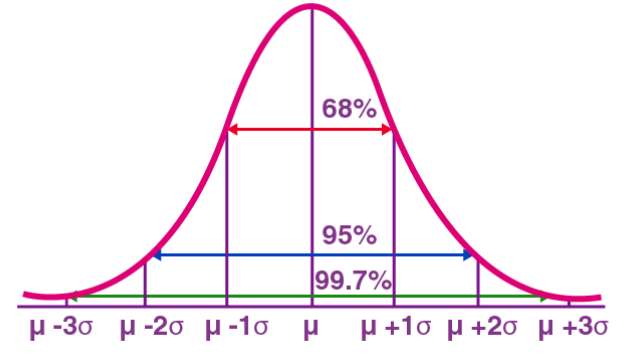
正态分布(Normal Distribution),也被称为高斯分布(Gaussian Distribution),是一种连续型概率分布。它具有一个对称的钟形曲线,以均值(μ)为中心,标准差(σ)为宽度。正态分布在统计学、概率论、工程学等多个领域具有重要的应用价值。
正态分布的概率密度函数可以表示为:
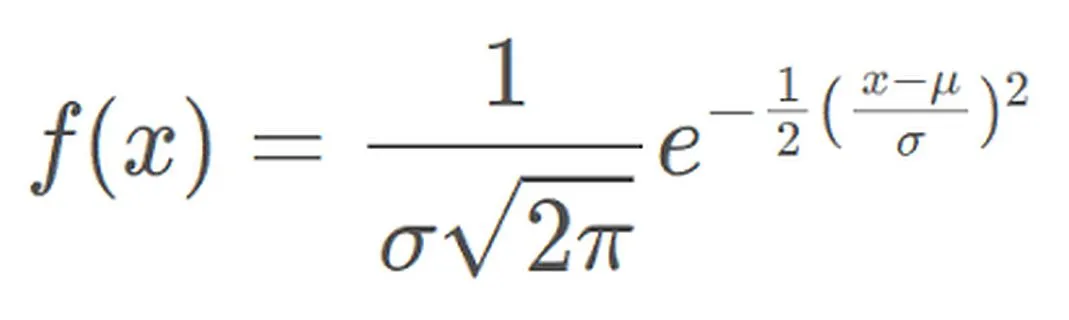
概率密度函数表示在给定值x附近的单位区间内正态分布的随机变量取值的概率密度。其中,μ表示均值,σ表示标准差
正态分布在实际中的应用是广泛的。例如,人的身高和体重分布近似于正态分布。此外,考试成绩通常呈正态分布,高分和低分的人数较少,而中间分数的人数较多。这种分布模式在许多领域都有重要的应用价值
2. 伯努利分布
伯努利分布(Bernoulli Distribution)是一种离散型概率分布,用于描述只有两种可能结果的单次随机试验。伯努利试验可以是正面或反面,成功或失败,是或否等。例如,抛硬币、检测产品是否合格、某人是否购买某种产品等。
伯努利分布的概率质量函数为:
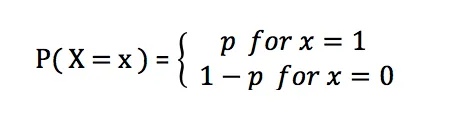
在伯努利分布中,p表示成功的概率,其取值范围为0到1。当p等于0.5时,伯努利分布就趋近于均匀分布
伯努利分布在实际中的应用:例如二项分布就是伯努利分布的n次独立重复试验。
3. 二项分布
二项分布(Binomial Distribution)是一种离散型概率分布,用于描述在n次独立重复试验中成功次数的概率分布。每次试验只有两种可能的结果:成功(记为1)或失败(记为0)。成功的概率为p,失败的概率为1-p。
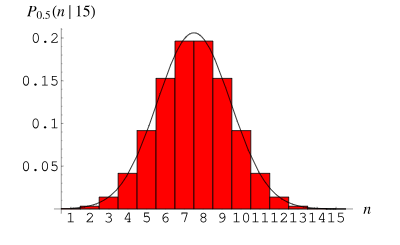
二项分布的概率质量函数可以表示为:
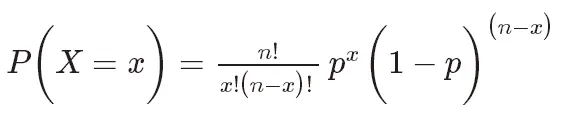
其中,P(X=k)表示成功次数为k的概率,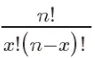 是组合数,表示从n次试验中选择k次成功的组合数。p是成功的概率,取值范围在0和1之间。n是试验次数。
是组合数,表示从n次试验中选择k次成功的组合数。p是成功的概率,取值范围在0和1之间。n是试验次数。
二项分布在实际中的应用非常广泛。举例来说,在医学研究中,我们可以利用二项分布来计算患者接受某种治疗的成功率。在工程领域中,我们可以使用二项分布来评估产品在生产过程中的合格率。这些都是二项分布在实际应用中的重要例子
4. 泊松分布
泊松分布(Poisson Distribution)是一种离散型概率分布,用于描述在固定时间内,事件发生的次数的概率分布。泊松分布适用于那些事件相互独立,且平均发生速率恒定的情况。
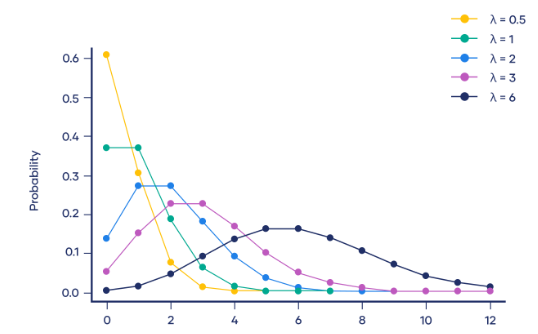
泊松分布的概率密度函数是:
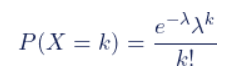
在这里,P(X=k)代表在固定时间内事件发生k次的概率,λ表示事件的平均发生速率,也就是单位时间内事件发生的平均次数。e是自然常数,约等于2.718。k表示事件发生的次数
泊松分布在实际中的应用十分广泛,比如在电话呼叫中心,每分钟打进的电话数量可以看作是泊松分布,其中平均每分钟打进的电话数量为λ
5. 指数分布
指数分布(Exponential Distribution)是一种连续型概率分布,用于描述在固定时间内,事件发生的概率。指数分布适用于那些事件相互独立,且平均发生速率恒定的情况。
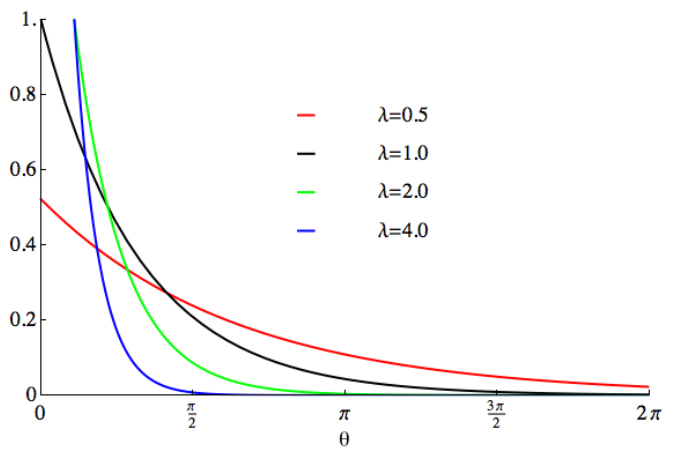
指数分布的概率密度函数为:
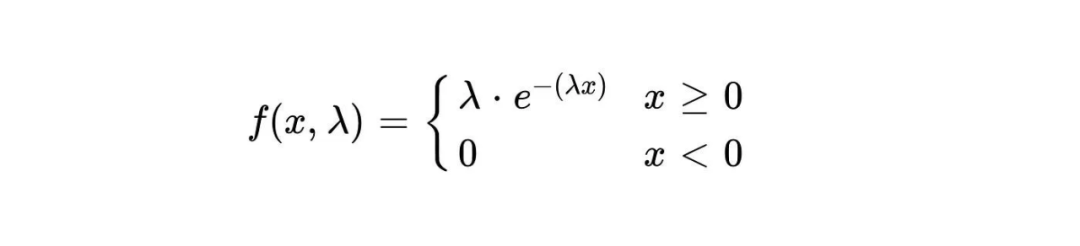
在给定时间x内事件发生的概率密度用f(x,λ)表示。λ表示事件的平均发生速率,即单位时间内事件发生的平均次数。e是自然常数,约等于2.718
指数分布在现实生活中有许多应用。例如,在放射性衰变中,放射性原子核的衰变时间可以被视为指数分布。这意味着衰变时间的概率分布符合指数函数。而平均衰变时间则对应着指数函数的参数λ
6. 伽玛分布
Gamma分布是一种连续概率分布,用于描述事件在给定时间内发生的概率。它适用于事件之间互相独立,并且平均发生速率始终不变的情况
伽玛分布的概率密度函数为:
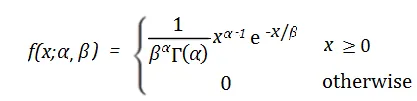
在此其中,f(x)代表在特定时间x内事件发生的概率密度。α和β是伽玛分布的形状参数和速率参数。α用于决定伽玛分布的形状,取值范围为0到正无穷。β表示事件的平均发生速率,即在单位时间内事件发生的平均次数,取值范围为0到正无穷。e为自然常数,约等于2.718
伽玛分布在实际中的应用:例如放射性衰变:在放射性衰变中,放射性原子核衰变的时间可以看作是伽玛分布,平均衰变时间即为β/α。
7. 贝塔分布
贝塔分布(Beta distribution)是一种连续型概率分布,用于描述一组数值中成功次数的概率分布。它具有两个参数,分别表示成功概率的期望值(mean)和标准差(standard deviation)。
贝塔分布的概率密度函数如下:
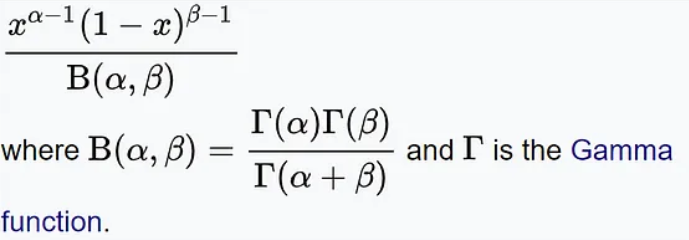
在这其中,x代表成功的次数,α和β分别代表分布的形状参数
贝塔分布在许多实际问题中都有应用。例如,在基因编辑中,研究人员可能会使用贝塔分布来预测基因编辑技术成功编辑某个目标位点的概率。在金融领域,贝塔分布可以用于描述资产价格的波动性,或者用于计算投资组合的预期收益
8. 均匀分布
均匀分布是一种概率分布,用于描述一组数值在某个区间内均匀地分布。均匀分布有两种类型:离散均匀分布和连续均匀分布。
离散均匀分布:当一个离散随机变量X满足以下概率分布时:P(X=k) = k/(n+1),其中k为非负整数,n为区间内的整数,我们称X服从离散均匀分布。连续均匀分布:当一个连续随机变量X的概率密度函数为f(x) = 1/(b-a)时,我们称X服从连续均匀分布,其中a和b为区间的两个端点
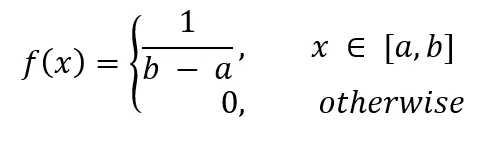
均匀分布的特点是,在给定的区间内,每个数值都有相同的机会出现。例如,抛一枚公正的硬币,正面和反面出现的概率都是1/2,这就是一种均匀分布。

9. 对数正态分布
对数正态分布(Log-normal distribution)是一种连续型概率分布,它的特点是随机变量的对数服从正态分布。换句话说,如果一个随机变量X的对数ln(X)服从正态分布,那么这个随机变量X就服从对数正态分布。
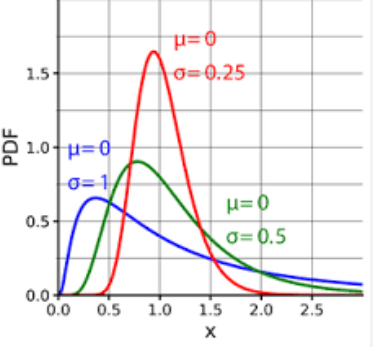
对数正态分布的概率密度函数可以表示为:
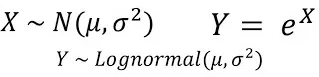
其中,μ是对数正态分布的均值,σ是对数正态分布的标准差。
对数正态分布在许多实际应用中都有重要意义,例如金融领域(股票价格、收益率等)、生物学(生长速率等)、经济学(消费支出等)等。
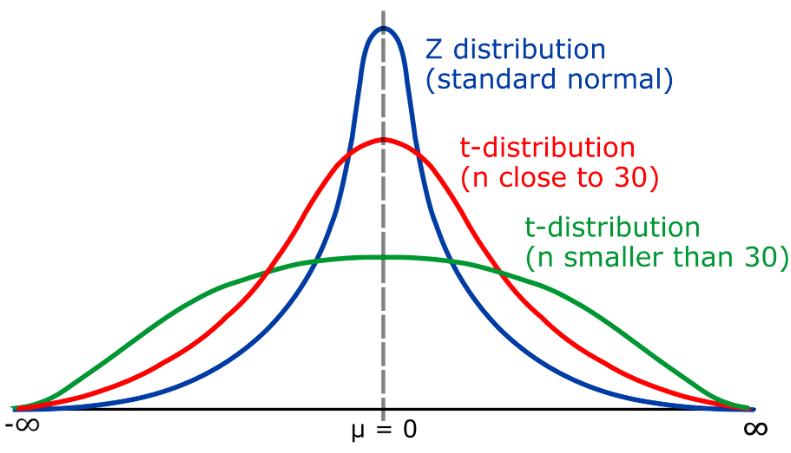
10. T分布
T分布,是一种连续型概率分布,主要用于小样本情况下描述均值的分布。t分布与正态分布(Normal distribution)类似,但它的尾部可以向左右延伸,取决于自由度(k)的大小。t分布广泛应用于统计推断,例如在假设检验中用于评估样本均值与总体均值之间的显著性差异。
t分布的期望和方差如下:
E(t)=0
要重写的内容是:Var(t)=k/(k-1)
t分布的自由度(k)表示样本大小(n)和总体标准差之间的关系。当k > 30时,t分布接近正态分布;当k接近1时,t分布变为柯西分布(Cauchy分布)
在实际应用中,当样本量较大(n>30)时,可以使用正态分布进行假设检验,这时可以利用z统计量建立置信区间。然而,当样本量较小(n
11. Weibull分布
Weibull分布(Weibull distribution)是一种连续型概率分布。
Weibull分布的概率密度函数为:
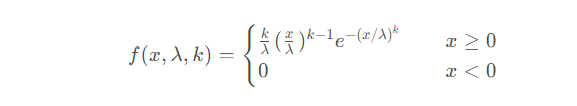
在韦伯分布中,x被视为随机变量,λ则被称为比例参数(scale),k则是形状参数(shape)。就韦伯分布而言,当k等于1时,它就是指数分布。如果λ等于1的话,这就是最小化的韦伯分布
以上是11个基本分布,数据科学家95%的时间都在使用的详细内容。更多信息请关注PHP中文网其他相关文章!

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

热门话题
 使用pandas读取CSV文件并进行数据分析
Jan 09, 2024 am 09:26 AM
使用pandas读取CSV文件并进行数据分析
Jan 09, 2024 am 09:26 AM
Pandas是一个强大的数据分析工具,可以方便地读取和处理各种类型的数据文件。其中,CSV文件是最常见和常用的数据文件格式之一。本文将介绍如何使用Pandas读取CSV文件并进行数据分析,同时提供具体的代码示例。一、导入必要的库首先,我们需要导入Pandas库和其他可能需要的相关库,如下所示:importpandasaspd二、读取CSV文件使用Pan
 数据分析方法介绍
Jan 08, 2024 am 10:22 AM
数据分析方法介绍
Jan 08, 2024 am 10:22 AM
常见的数据分析方法:1、对比分析法;2、结构分析法;3、交叉分析法;4、趋势分析法;5、因果分析法;6、关联分析法;7、聚类分析法;8、主成分分析法;9、散点分析法;10、矩阵分析法。详细介绍:1、对比分析法:将两个或两个以上的数据进行对比分析,找出其中的差异和规律;2、结构分析法:对总体内各部分与总体之间进行对比分析的方法;3、交叉分析法等等。
 11个基本分布,数据科学家95%的时间都在使用
Dec 15, 2023 am 08:21 AM
11个基本分布,数据科学家95%的时间都在使用
Dec 15, 2023 am 08:21 AM
继上次盘点《数据科学家95%的时间都在使用的11个基本图表》之后,今天将为大家带来数据科学家95%的时间都在使用的11个基本分布。掌握这些分布,有助于我们更深入地理解数据的本质,并在数据分析和决策过程中做出更准确的推断和预测。1.正态分布正态分布(NormalDistribution),也被称为高斯分布(GaussianDistribution),是一种连续型概率分布。它具有一个对称的钟形曲线,以均值(μ)为中心,标准差(σ)为宽度。正态分布在统计学、概率论、工程学等多个领域具有重要的应用价值。
 使用Go语言进行机器学习和数据分析
Nov 30, 2023 am 08:44 AM
使用Go语言进行机器学习和数据分析
Nov 30, 2023 am 08:44 AM
在当今智能化的社会中,机器学习和数据分析是必不可少的工具,能够帮助人们更好地理解和利用大量的数据。而在这些领域中,Go语言也成为了备受关注的一种编程语言,它的速度和效率使它成为了很多程序员的选择。本文介绍如何使用Go语言进行机器学习和数据分析。一、机器学习Go语言的生态系统并不像Python和R那样丰富,但是,随着越来越多的人开始使用它,一些机器学习库和框架
 数据分析和机器学习的11个高级可视化图表介绍
Oct 25, 2023 am 08:13 AM
数据分析和机器学习的11个高级可视化图表介绍
Oct 25, 2023 am 08:13 AM
可视化是一种强大的工具,用于以直观和可理解的方式传达复杂的数据模式和关系。它们在数据分析中发挥着至关重要的作用,提供了通常难以从原始数据或传统数字表示中辨别出来的见解。可视化对于理解复杂的数据模式和关系至关重要,我们将介绍11个最重要和必须知道的图表,这些图表有助于揭示数据中的信息,使复杂数据更加可理解和有意义。1、KSPlotKSPlot用来评估分布差异。其核心思想是测量两个分布的累积分布函数(CDF)之间的最大距离。最大距离越小,它们越有可能属于同一分布。所以它主要被解释为确定分布差异的“统
 如何利用ECharts和php接口实现统计图的数据分析和预测
Dec 17, 2023 am 10:26 AM
如何利用ECharts和php接口实现统计图的数据分析和预测
Dec 17, 2023 am 10:26 AM
如何利用ECharts和php接口实现统计图的数据分析和预测数据分析和预测在各个领域中扮演着重要角色,它们能够帮助我们理解数据的趋势和模式,为未来的决策提供参考。ECharts是一款开源的数据可视化库,它提供了丰富灵活的图表组件,可以通过使用php接口来实现数据的动态加载和处理。本文将介绍基于ECharts和php接口的统计图数据分析和预测的实现方法,并提供
 Python 与机器学习的浪漫之旅,从新手到专家的一步之遥
Feb 23, 2024 pm 08:34 PM
Python 与机器学习的浪漫之旅,从新手到专家的一步之遥
Feb 23, 2024 pm 08:34 PM
1.Python与机器学习的邂逅python作为一种简单易学、功能强大的编程语言,深受广大开发者的喜爱。而机器学习作为人工智能的一个分支,旨在让计算机学会如何从数据中学习并做出预测或决策。Python与机器学习的结合,可谓是珠联璧合,为我们带来了一系列强大的工具和库,使得机器学习变得更加容易实现和应用。2.Python机器学习库探秘Python中提供了众多功能丰富的机器学习库,其中最受欢迎的包括:NumPy:提供了高效的数值计算功能,是机器学习的基础库。SciPy:提供了更高级的科学计算工具,是
 哪些行业对Go语言需求较大?
Feb 21, 2024 pm 10:39 PM
哪些行业对Go语言需求较大?
Feb 21, 2024 pm 10:39 PM
在当今快速发展的科技时代,各种编程语言的应用范围日益广泛,其中Go语言作为一种高效、简洁、易于学习和使用的编程语言,受到越来越多企业和开发者的青睐。Go语言(也称为Golang)是由Google开发的一种编程语言,它强调简洁、高效和并发编程,适用于各种应用场景。那么,哪些行业对Go语言的需求较大呢?接下来将分析一些主要行业,并探讨它们对Go语言的需求。互联网






