DeepMind论文登上Nature：困扰数学家几十年的难题，大模型发现全新解

作为今年人工智能领域的顶尖技术，大型语言模型（LLM）擅长于将概念进行组合，并通过阅读、理解、写作和编码来帮助人们解决问题。但是，它们是否能够发现全新的知识呢？

鉴于LLM已被证明存在"幻觉"问题，即生成与事实不符的信息，因此利用LLM进行可验证的正确发现是一项具有挑战性的任务

现在，来自 Google DeepMind 的研究团队提出了一种为数学和计算机科学问题搜索解决方案的新方法 ——FunSearch。FunSearch 的工作原理是将预训练的 LLM（以计算机代码的形式提供创造性解决方案）与自动「评估器」配对，以防止产生幻觉和错误思路。通过在这两个组件之间来回迭代，最初的解决方案演变成了「新的知识」。相关论文发表在《自然》杂志上。

论文地址：https://www.nature.com/articles/s41586-023-06924-6

这项工作是首次利用 LLM 在科学或数学的挑战性开放问题方面取得新发现。

FunSearch 发掘出全新的 cap set 问题解决方案，这是数学领域中一直存在的未解决问题。此外，DeepMind 还借助该解决方案，探索出更加高效的算法来解决「装箱」问题，该问题在许多领域都有广泛应用，例如数据中心的效率提升。展示了 FunSearch 的实际应用价值

研究团队认为 FunSearch 将成为一个特别强大的科学工具，因为它输出的程序揭示了其解决方案是如何构建的，而不仅仅是解决方案是什么。这将会激发科学家的进一步见解，从而形成科学改进与发现的良性循环。

通过语言模型的进化推动发现

FunSearch 采用了由 LLM 支持的进化算法，以鼓励和推动得分最高的创意和思路。这些创意和思路可以被表达为计算机程序，以便它们可以自动运行和评估

首先，用户需要将问题的描述以代码的形式编写出来。这个描述应该包括评估程序的过程以及用于初始化程序池的种子程序

FunSearch是一个不断迭代的过程。在每次迭代中，系统会从当前的程序池中选择一些程序，并将其传递给LLM。LLM会在此基础上进行构建并生成新的程序，然后自动进行评估。最佳的程序将被添加回到现有的程序库中，从而形成一个自我改进的循环。FunSearch使用了Google的PaLM 2，但也兼容其他接受过代码训练的方法

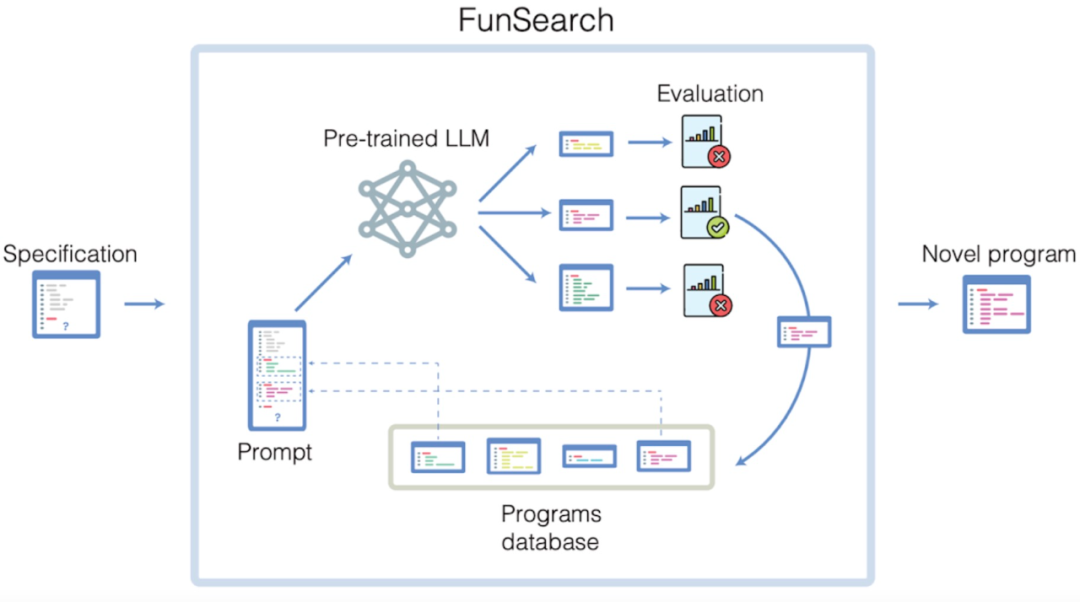
LLM 会从程序数据库中检索出生成的最佳程序，并被要求生成一个更好的程序。

众所周知，在各个领域中探索新的数学知识和算法是非常具有挑战性的任务，往往超出目前最先进的人工智能系统的能力范围。为了让FunSearch能够胜任这一任务，该研究团队引入了多个关键组件。FunSearch并非从零开始，而是从问题的常识出发，通过进化过程来专注于寻找最关键的想法以实现新的发现

此外，FunSearch 的进化过程使用一种策略来提高想法的多样性，以避免出现停滞情况。最后，为了提高系统效率，进化过程是并行运行的。

在数学领域开辟新天地

DeepMind 表示，他们首先要解决的是 Cap set 问题，这是一个开放性难题，几十年来一直困扰着多个研究领域的数学家。知名数学家陶哲轩曾把它描述为自己最喜欢的开放性问题。DeepMind 选择与威斯康星大学麦迪逊分校的数学教授 Jordan Ellenberg 合作，他是 Cap set 问题的重要突破者。

一个重要的问题是在高维网格中寻找最大的点集（称为“cap set”），使得其中没有三个点共线。这个问题的重要性在于它可以作为极值组合学中其他问题的模型。极值组合学研究集合可能具有的最小或最大大小，这些集合可以是数字、图形或其他对象。暴力解法无法解决此问题——需要考虑的可能性数量很快就会超过宇宙中原子的数量

FunSearch 以程序形式生成的解决方案在某些情况下发现了有史以来最大的 cap set。这代表了过去 20 年中 cap set 规模的最大增长。此外，FunSearch 的性能超过了最先进的计算求解器，因为这个问题的规模远远超出了它们目前的能力。

交互式图表显示了从种子程序（上）到新的高分函数（下）的演变。每个圆圈都代表一个程序，其大小与分配给它的分数成正比。图中仅显示底部程序的上级。FunSearch 为每个节点生成的相应函数如右侧所示。

这些结果表明，FunSearch 技术可以让人类超越困难组合问题的既定结果，而在这些问题上很难建立直觉。DeepMind 期望这种方法能够在组合学中类似理论问题的新发现中发挥作用，并在未来为通信理论等领域带来新的可能性。

FunSearch 偏好简洁、可由人类理解的程序

尽管发现新的数学知识本身意义重大，但与传统的计算机搜索技术相比，FunSearch 方法还展现出了其他的优势。这是因为，FunSearch 并不是一个只会生成问题解决方案的黑箱。相反，它生成的程序会描述出这些解决方案是如何得出的。这种「show-your-working」通常是科学家的工作方式，他们通过阐述产生新发现或新现象的过程来解释这些发现或现象。

FunSearch更倾向于寻找具有较低Kolmogorov复杂度的解决方案，这些解决方案代表了高度紧凑的程序。Kolmogorov复杂度是指输出解所需要的最短计算机程序的长度。通过使用简短的程序，FunSearch可以描述非常大的对象，从而能够处理非常复杂的问题。此外，这也使得研究人员更容易理解FunSearch生成的程序输出。Ellenberg表示：「FunSearch提供了一种全新的机制来制定打击策略。通过FunSearch生成的解决方案在概念上比单纯的数字列表更为丰富。通过研究它们，我学到了一些东西。」

更重要的是，FunSearch 程序的这种可解释性可以为研究人员提供可操作的见解。例如，DeepMind 在使用 FunSearch 的过程中注意到，它的一些高分输出的代码中存在耐人寻味的对称性。这让 DeepMind 对问题有了新的认识，他们利用这种认识改进了引入 FunSearch 的问题，从而找到了更好的解决方案。DeepMind 认为，这是人类与 FunSearch 在数学领域的许多问题上进行合作的典范。

左图：通过检查 FunSearch 生成的代码，DeepMind 获得了更多可操作的见解（高亮部分）。右图：使用（更短的）左图程序构造的原始「可接受」集合。

解决一个众所周知的计算难题

在理论 cap set 问题取得成功的鼓舞下，DeepMind 决定将 FunSearch 应用于计算机科学中一个重要的实际挑战 —— 装箱问题（bin packing），以探索它的灵活性。装箱问题关注的是如何将不同尺寸的物品打包到最少数量的箱子中。它是许多现实世界问题的核心，从装载物品的集装箱到数据中心的计算工作分配，这些场景都需要最大限度地降低成本。

通常，解决在线装箱问题会使用基于人类经验的启发式算法规则。然而，针对每种特定情况（大小、时间或容量各不相同）制定一套规则是非常具有挑战性的。虽然与 cap set 问题有很大不同，但是使用 FunSearch 来解决这个问题非常容易。FunSearch 提供了一个自动定制的程序，可以根据具体情况适应数据，相较于现有的启发式方法，它能够使用更少的箱子来装载相同数量的物品

使用现有启发式 ——Best-fit 启发式（左）和 FunSearch 发现的启发式（右）进行装箱的示例。

像在线装箱这样的复杂组合问题可以使用其他人工智能方法来解决，比如神经网络和强化学习。这些方法也被证明是有效的，但也可能需要大量的资源来部署。另一方面，FunSearch 输出的代码易于检查和部署，这意味着它的解决方案有可能被应用到各种现实工业系统中，从而迅速带来效益。

DeepMind：用大模型应对科学挑战将成普遍做法

FunSearch 证明，如果能防止 LLM 产生幻觉，那么这些模型的力量不仅可以用来产生新的数学发现，还可以用来揭示重要现实问题的潜在解决方案。

DeepMind 认为，对于科学和工业领域的许多问题 —— 无论是长期存在的问题还是新问题 —— 使用 LLM 驱动的方法生成有效和量身定制的算法将成为普遍做法。

其实，这仅仅是一个开始。随着 LLM 不断取得进展，FunSearch 也将不断完善。DeepMind 表示，他们还将努力扩展其功能，以应对社会上各种紧迫的科学和工程挑战。

以上是DeepMind论文登上Nature：困扰数学家几十年的难题，大模型发现全新解的详细内容。更多信息请关注PHP中文网其他相关文章！