幂级数的和函数并级数的和
幂级数的和函数并级数的和
首先要注意的是,对于-1 为了帮助大家更好地理解,我们来逐项积分得到如下结果:
-ln(1-x) = ∑{0 ≤ n} x^(n+1)/(n+1) = ∑{1 ≤ n} x^n/n (由ln(1) = 0可确定积分常数)。
通过这个公式,我们可以计算出-ln(1-x)的值,这有助于解决一些数学问题。希望这个方法对大家有所帮助! 为了帮助还没有解开谜题的玩家们,让我们一起来了解一下具体的解谜方法吧。其中关键的一步是将方程转化为形式为“于是-x·ln(1-x) = ∑{1 ≤ n} x^(n+1)/n = ∑{2 ≤ n} x^n/(n-1)”的等式。这一步的关键是使用级数展开的方式,通过对幂级数的求和来得到等式的右边部分。 为了帮助大家更好地理解,让我们一起解读一下这个数学公式的具体含义:$ln(1-x)/x = sum_{1 leq n} frac{x^{n-1}}{n} = sum_{0 leq n} frac{x^n}{n+1} = 1+frac{x}{2}+sum_{2 leq n} frac{x^n}{n+1}。 为了帮助大家更好地理解这个公式,我们可以通过推导和演算来证明它的正确性。具体的步骤如下:
首先,我们可以将右侧的级数展开为无穷级数。这个级数可以通过将每一项的系数展开成一个等比数列来表示。
接下来,我们可以将左侧的表达式进行化简。利用级数的性质,我们可以将它表示为一个分数的形式。
然后,我们可以通过 为了帮助大家更好地理解,我们可以将等式化简为ln(1-x)/x+1+x/2-x·ln(1-x) = 2·∑{2 ≤ n} x^n/(n²-1)。这样我们就可以更清楚地看到等式的结构和关系了。 ∑{2 ≤ n} x^n/(n²-1) = ln(1-x)/(2x) + 1/2 + x/4 - x·ln(1-x)/2 这个级数在闭区间(-1,1)内一致收敛。 代入x = 1/2后,我们得到了∑{2 ≤ n} 1/((n²-1)2^n) = 5/8-3ln(2)/4的结果。这个结果可以帮助我们解决具体的问题。 1,令an=x^n/n(n-1) 根据给定的公式,我们可以推导出以下结论:当x=1时,an=1/n(n-1)=1/(n-1)-1/n,这个级数是收敛的。而当x=-1时,an=(-1)^n*(1/(n-1)-1/n)也是收敛的,这是一个交错级数。 故收敛区间为[-1,1] 2,这个题目应该从第2项到无穷吧?不然无意义。 由于an=x^n/n(n-1)=x^n[1/(n-1)-1/n]=x^n/(n-1)-x^n/n 为了帮助还没有过关的玩家们,让我们一起来了解一下具体的解谜方法吧。在解谜过程中,请注意从n=2开始计算和,并根据公式第2项为-x-ln(1-x)。此外,第一项可以写成(x^(n-1))*x/(n-1),然后推导出-xln(1-x)。希望这些小技巧能帮助大家顺利解决难题。 为了帮助那些还没有解开谜题的玩家们,让我们一起来了解一下具体的解谜方法吧。解谜的关键在于将整个级数和转化为更简单的形式,具体的计算过程如下:整个级数和为-xln(1-x)-(-x-ln(1-x))=(1-x)ln(1-x)+x。通过这个方法,你将更容易理解和解决谜题。 解:【用 [.]'表示对x导】。 让我们一起来了解一下如何解析这个表达式:原始式为∑[(-1)^n]x^(2n)+2∑{[(-1)^n]/[2n(2n-1)]}x^(2n)。现在我们来详细讲解一下具体的解谜方法。 为了帮助大家更好地理解,我们来探讨一下在收敛域内的求和公式:∑[(-1)^n]x^(2n)=(-x^2)/(1+x^2)。 设S=∑{[(-1)^n]/[2n(2n-1)]}x^(2n),对x求导得S'=∑{[(-1)^n]/(2n-1)}x^(2n-1)。再对x求导得S''=∑[(-1)^n]x^(2n-2)=-1/(1+x^2)。 根据解题过程,我们得到了最终的结果:S = -xarctanx + (1/2)ln(1+x^2) + C。其中,C是常数。另外,根据题目中给出的条件,我们可以确定C的值为0。 以下是原式的解谜方法供参考:我们可以使用一些数学公式和性质来简化和求解这个表达式。首先,我们可以利用三角函数的关系将-arctan(x)转换为-ln(cos(arctan(x)))。然后,我们可以将-arctan(x)和ln(1+x^2)合并为一个对数函数ln((1+x^2)/cos(arctan(x)))。接下来,我们可以将-ln(cos(arctan(x)))和-ln((1+x^2)/cos(arctan(x)))合并为一个对数函数幂级数和函数问题
幂级数的和函数
以上是幂级数的和函数并级数的和的详细内容。更多信息请关注PHP中文网其他相关文章!

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

热门话题
 如何编辑注册表? (警告:谨慎使用!)
Mar 21, 2025 pm 07:46 PM
如何编辑注册表? (警告:谨慎使用!)
Mar 21, 2025 pm 07:46 PM
文章讨论了编辑Windows注册表,预防措施,备份方法以及不正确的编辑中的潜在问题。主要问题:系统不稳定和数据丢失的风险不当变化。
 发现如何在Windows设置中修复驱动健康警告
Mar 19, 2025 am 11:10 AM
发现如何在Windows设置中修复驱动健康警告
Mar 19, 2025 am 11:10 AM
Windows设置中的驱动器健康警告是什么意思?收到磁盘警告时该怎么办?阅读本php.cn教程以获取逐步说明以应对这种情况。
 哪个应用程序使用ene.sys
Mar 12, 2025 pm 01:25 PM
哪个应用程序使用ene.sys
Mar 12, 2025 pm 01:25 PM
本文将ene.sys视为Realtek高清音频驱动程序组件。 它详细介绍了其在管理音频硬件方面的功能,并强调了其在音频功能中的关键作用。 该文章还指导用户验证其合法性
 如何使用组策略编辑器(gpedit.msc)?
Mar 21, 2025 pm 07:48 PM
如何使用组策略编辑器(gpedit.msc)?
Mar 21, 2025 pm 07:48 PM
本文介绍了如何在Windows中使用组策略编辑器(GPEDIT.MSC)来管理系统设置,突出显示常见的配置和故障排除方法。它指出gpedit.msc在Windows Home Edition中不可用,建议
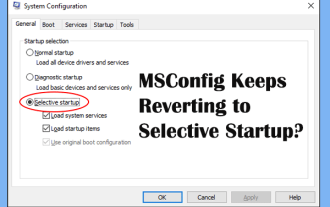 MSCONFIG不断恢复为选择性启动吗? 2个解决方案
Mar 28, 2025 pm 12:06 PM
MSCONFIG不断恢复为选择性启动吗? 2个解决方案
Mar 28, 2025 pm 12:06 PM
您是否质疑Msconfig不断恢复到窗口上的选择性启动的问题?如果需要,如何切换到普通启动?尝试在此php.cn帖子中解释的方法,以找到适合您的方法。
 Windows元数据和Internet服务问题:如何解决?
Apr 02, 2025 pm 03:57 PM
Windows元数据和Internet服务问题:如何解决?
Apr 02, 2025 pm 03:57 PM
您可能会看到“无法建立与Windows Metadata和Internet Services(WMI)的连接”。事件查看器的错误。 PHP.CN的这篇文章介绍了如何删除Windows元数据和Internet服务问题。








