详解matlab下非线性方程组迭代法的实现方法

详解matlab下非线性方程组迭代法的实现方法

牛顿迭代法：

function[x0,n]=newton(fx,dfx,x0,tol,N)

% 牛顿迭代法

% 第一个参数 fx 是关于变量x的所要的函数表达式.

% 第二个参数 dfx 是fx的一阶导数.

% x0 是迭代初始值.

% tol 是迭代误差限.

% N 最大迭代次数.

x=x0;f0=eval(fx);df0=eval(dfx);

n=0;

disp('[ n xn xn+1 delta ]');

while n

x1=x0-f0/df0;

x=x1;f1=eval(fx);df1=eval(dfx);

delta=abs(x0-x1);

% X=[n,x0,x1,delta];

disp(X)； %用于显示中间结果

if delta

fprintf（'迭代计算成功'）

return

else

n=n+1;

x0=x1;f0=f1;df0=df1;

end

end

if n==N+1

fprintf（'迭代计算失败 '）

end

另外两个在此基础上稍作改动就可以了。

MATLAB用牛顿迭代解非线性方程的程序

给你一个完整版：

% 牛顿法解非线性方程组

function main()

clc; clear all;

f = @(x)log(x+sin(x)）； % 测试函数

df = @(x)(1+cos(x))/(x+sin(x)）； % 导数函数

x0 = 0.1； % 迭代初值

x = TestNewton(f, df, x0) % 牛顿法解

function x = TestNewton(fname, dfname, x0, e, N)

% 用途：Newton迭代法解非线性方程f(x)=0

% fname和dfname分别表示f(x)及其导函数的M函数句柄或内嵌函数表达式

% x0为迭代初值，e为精度（默认值1e-7）

% x为返回数值解，并显示计算过程，设置迭代次数上限N以防发散（默认500次）

% 输入参数

if nargin

N = 500;

end

if nargin

e = 1e-7;

end

x = x0； % 初值

x0 = x+2*e； % 浮动

k = 0； % 步数

fprintf('x[%d]=%12.9fn', k, x) % 打印信息

while abs(x0-x)>e & k

k = k+1； % 记录步数

x0 = x； % 更新x(k)

x = x0 - feval(fname,x0)/feval(dfname,x0)； % 更新x(k+1)

fprintf('x[%d]=%12.9fn', k, x) % 打印信息

end

if k == N

fprintf（'已达到迭代次数上限'）； % 迭代结束

end

结果：

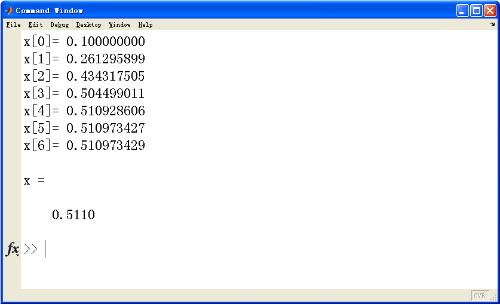
以上是详解matlab下非线性方程组迭代法的实现方法的详细内容。更多信息请关注PHP中文网其他相关文章！