使用Python编写B+树的删除操作代码
b树的概念
B+树删除操作需要先找到删除节点的位置，然后判断节点的键数。
如果节点中的键数量超过了最小数量，直接删除即可。
如下图，删除“40”：
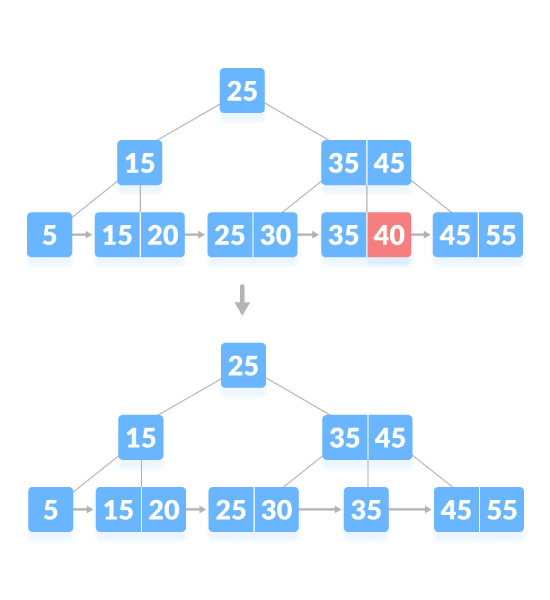
如果节点中有确切的最小键数，删除就需要从兄弟节点那里借用，将兄弟节点的中间键添加到父节点。如下图，删除“5”：
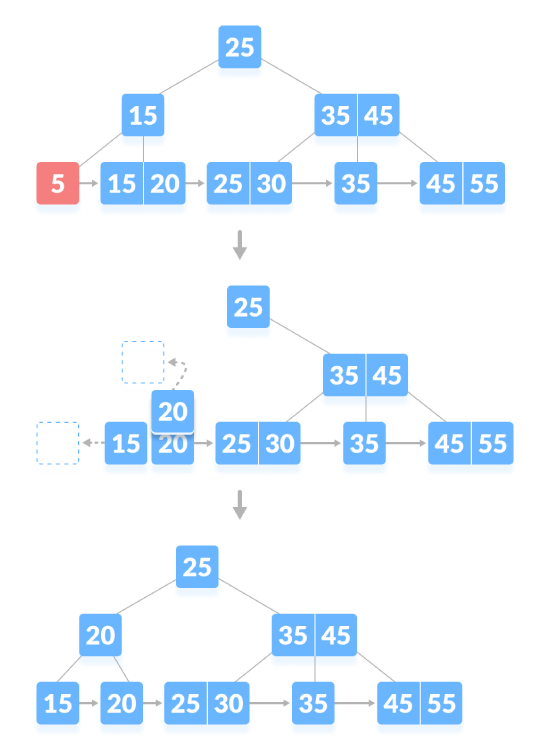
删除内容节点，如果节点中的键数超过最小数量，只需从叶节点中删除该键，并从内部节点中删除该键。用中序后继填充内部节点中的空白区域。如下图，删除“45”：
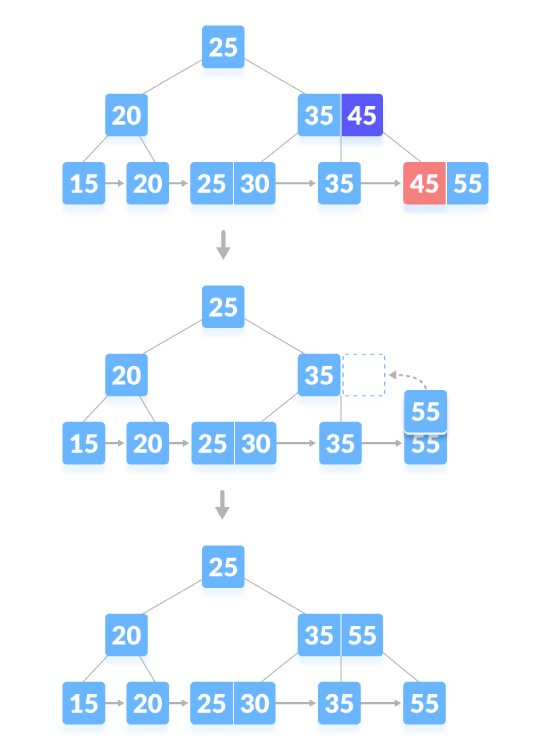
删除内容节点，如果节点中有确切的最小键数，则删除该键并直接从兄弟节点借用一个键，用借来的键填充索引中的空白空间。如下图，删除“35”：
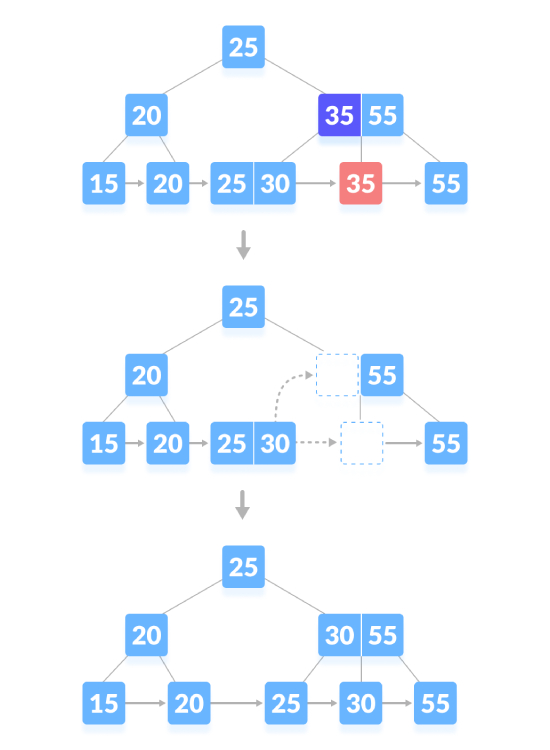
删除内容节点，在父节点上方生成空白空间。删除键后，将空白空间与其兄弟节点合并，用中序后继填充父节点中的空白空间。如下图，删除“25”：
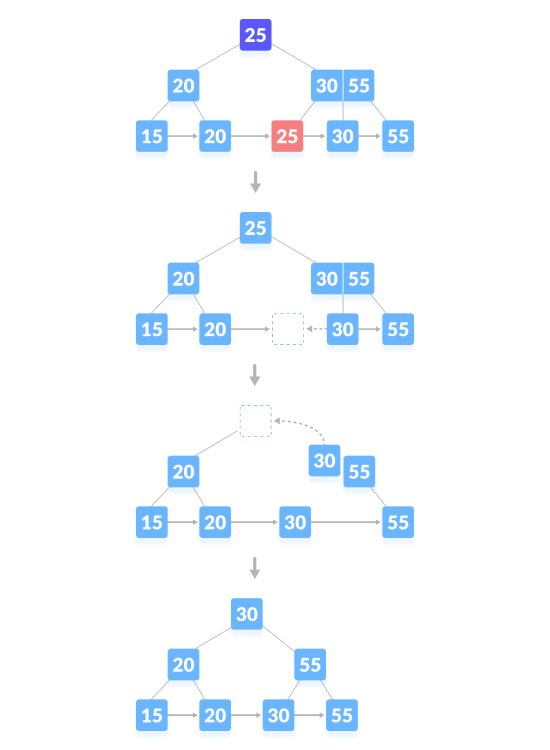
导致树高度会缩小的删除操作，如下图，删除“55”：
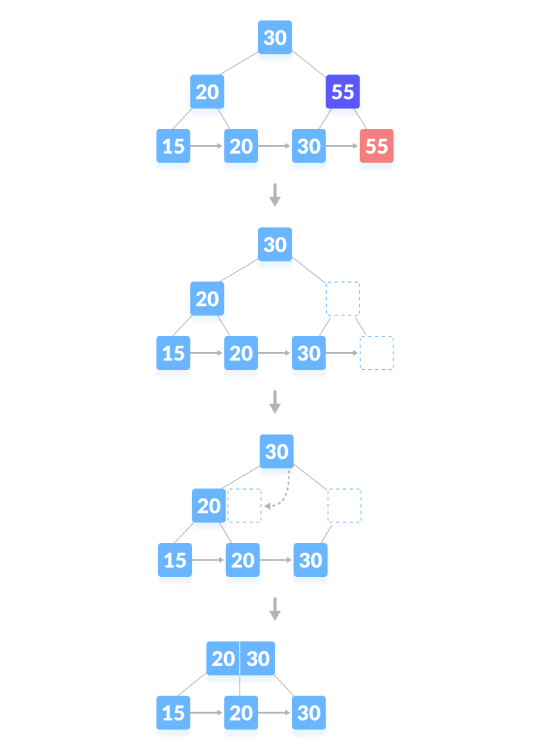
Python实现B+树删除操作
import math
# 创建节点
class Node:
def __init__(self, order):
self.order = order
self.values = []
self.keys = []
self.nextKey = None
self.parent = None
self.check_leaf = False
# 插入叶子
def insert_at_leaf(self, leaf, value, key):
if (self.values):
temp1 = self.values
for i in range(len(temp1)):
if (value == temp1[i]):
self.keys[i].append(key)
break
elif (value < temp1[i]):
self.values = self.values[:i] + [value] + self.values[i:]
self.keys = self.keys[:i] + [[key]] + self.keys[i:]
break
elif (i + 1 == len(temp1)):
self.values.append(value)
self.keys.append([key])
break
else:
self.values = [value]
self.keys = [[key]]
# B+树
class BplusTree:
def __init__(self, order):
self.root = Node(order)
self.root.check_leaf = True
# 插入节点
def insert(self, value, key):
value = str(value)
old_node = self.search(value)
old_node.insert_at_leaf(old_node, value, key)
if (len(old_node.values) == old_node.order):
node1 = Node(old_node.order)
node1.check_leaf = True
node1.parent = old_node.parent
mid = int(math.ceil(old_node.order / 2)) - 1
node1.values = old_node.values[mid + 1:]
node1.keys = old_node.keys[mid + 1:]
node1.nextKey = old_node.nextKey
old_node.values = old_node.values[:mid + 1]
old_node.keys = old_node.keys[:mid + 1]
old_node.nextKey = node1
self.insert_in_parent(old_node, node1.values[0], node1)
def search(self, value):
current_node = self.root
while(current_node.check_leaf == False):
temp2 = current_node.values
for i in range(len(temp2)):
if (value == temp2[i]):
current_node = current_node.keys[i + 1]
break
elif (value < temp2[i]):
current_node = current_node.keys[i]
break
elif (i + 1 == len(current_node.values)):
current_node = current_node.keys[i + 1]
break
return current_node
# 查找节点
def find(self, value, key):
l = self.search(value)
for i, item in enumerate(l.values):
if item == value:
if key in l.keys[i]:
return True
else:
return False
return False
# 在父级插入
def insert_in_parent(self, n, value, ndash):
if (self.root == n):
rootNode = Node(n.order)
rootNode.values = [value]
rootNode.keys = [n, ndash]
self.root = rootNode
n.parent = rootNode
ndash.parent = rootNode
return
parentNode = n.parent
temp3 = parentNode.keys
for i in range(len(temp3)):
if (temp3[i] == n):
parentNode.values = parentNode.values[:i] + \
[value] + parentNode.values[i:]
parentNode.keys = parentNode.keys[:i +
1] + [ndash] + parentNode.keys[i + 1:]
if (len(parentNode.keys) > parentNode.order):
parentdash = Node(parentNode.order)
parentdash.parent = parentNode.parent
mid = int(math.ceil(parentNode.order / 2)) - 1
parentdash.values = parentNode.values[mid + 1:]
parentdash.keys = parentNode.keys[mid + 1:]
value_ = parentNode.values[mid]
if (mid == 0):
parentNode.values = parentNode.values[:mid + 1]
else:
parentNode.values = parentNode.values[:mid]
parentNode.keys = parentNode.keys[:mid + 1]
for j in parentNode.keys:
j.parent = parentNode
for j in parentdash.keys:
j.parent = parentdash
self.insert_in_parent(parentNode, value_, parentdash)
# 删除节点
def delete(self, value, key):
node_ = self.search(value)
temp = 0
for i, item in enumerate(node_.values):
if item == value:
temp = 1
if key in node_.keys[i]:
if len(node_.keys[i]) > 1:
node_.keys[i].pop(node_.keys[i].index(key))
elif node_ == self.root:
node_.values.pop(i)
node_.keys.pop(i)
else:
node_.keys[i].pop(node_.keys[i].index(key))
del node_.keys[i]
node_.values.pop(node_.values.index(value))
self.deleteEntry(node_, value, key)
else:
print("Value not in Key")
return
if temp == 0:
print("Value not in Tree")
return
# 删除条目
def deleteEntry(self, node_, value, key):
if not node_.check_leaf:
for i, item in enumerate(node_.keys):
if item == key:
node_.keys.pop(i)
break
for i, item in enumerate(node_.values):
if item == value:
node_.values.pop(i)
break
if self.root == node_ and len(node_.keys) == 1:
self.root = node_.keys[0]
node_.keys[0].parent = None
del node_
return
elif (len(node_.keys) < int(math.ceil(node_.order / 2)) and node_.check_leaf == False) or (len(node_.values) < int(math.ceil((node_.order - 1) / 2)) and node_.check_leaf == True):
is_predecessor = 0
parentNode = node_.parent
PrevNode = -1
NextNode = -1
PrevK = -1
PostK = -1
for i, item in enumerate(parentNode.keys):
if item == node_:
if i > 0:
PrevNode = parentNode.keys[i - 1]
PrevK = parentNode.values[i - 1]
if i < len(parentNode.keys) - 1:
NextNode = parentNode.keys[i + 1]
PostK = parentNode.values[i]
if PrevNode == -1:
ndash = NextNode
value_ = PostK
elif NextNode == -1:
is_predecessor = 1
ndash = PrevNode
value_ = PrevK
else:
if len(node_.values) + len(NextNode.values) < node_.order:
ndash = NextNode
value_ = PostK
else:
is_predecessor = 1
ndash = PrevNode
value_ = PrevK
if len(node_.values) + len(ndash.values) < node_.order:
if is_predecessor == 0:
node_, ndash = ndash, node_
ndash.keys += node_.keys
if not node_.check_leaf:
ndash.values.append(value_)
else:
ndash.nextKey = node_.nextKey
ndash.values += node_.values
if not ndash.check_leaf:
for j in ndash.keys:
j.parent = ndash
self.deleteEntry(node_.parent, value_, node_)
del node_
else:
if is_predecessor == 1:
if not node_.check_leaf:
ndashpm = ndash.keys.pop(-1)
ndashkm_1 = ndash.values.pop(-1)
node_.keys = [ndashpm] + node_.keys
node_.values = [value_] + node_.values
parentNode = node_.parent
for i, item in enumerate(parentNode.values):
if item == value_:
p.values[i] = ndashkm_1
break
else:
ndashpm = ndash.keys.pop(-1)
ndashkm = ndash.values.pop(-1)
node_.keys = [ndashpm] + node_.keys
node_.values = [ndashkm] + node_.values
parentNode = node_.parent
for i, item in enumerate(p.values):
if item == value_:
parentNode.values[i] = ndashkm
break
else:
if not node_.check_leaf:
ndashp0 = ndash.keys.pop(0)
ndashk0 = ndash.values.pop(0)
node_.keys = node_.keys + [ndashp0]
node_.values = node_.values + [value_]
parentNode = node_.parent
for i, item in enumerate(parentNode.values):
if item == value_:
parentNode.values[i] = ndashk0
break
else:
ndashp0 = ndash.keys.pop(0)
ndashk0 = ndash.values.pop(0)
node_.keys = node_.keys + [ndashp0]
node_.values = node_.values + [ndashk0]
parentNode = node_.parent
for i, item in enumerate(parentNode.values):
if item == value_:
parentNode.values[i] = ndash.values[0]
break
if not ndash.check_leaf:
for j in ndash.keys:
j.parent = ndash
if not node_.check_leaf:
for j in node_.keys:
j.parent = node_
if not parentNode.check_leaf:
for j in parentNode.keys:
j.parent = parentNode
# 输出B+树
def printTree(tree):
lst = [tree.root]
level = [0]
leaf = None
flag = 0
lev_leaf = 0
node1 = Node(str(level[0]) + str(tree.root.values))
while (len(lst) != 0):
x = lst.pop(0)
lev = level.pop(0)
if (x.check_leaf == False):
for i, item in enumerate(x.keys):
print(item.values)
else:
for i, item in enumerate(x.keys):
print(item.values)
if (flag == 0):
lev_leaf = lev
leaf = x
flag = 1
record_len = 3
bplustree = BplusTree(record_len)
bplustree.insert('5', '33')
bplustree.insert('15', '21')
bplustree.insert('25', '31')
bplustree.insert('35', '41')
bplustree.insert('45', '10')
printTree(bplustree)
if(bplustree.find('5', '34')):
print("Found")
else:
print("Not found")登录后复制
以上是使用Python编写B+树的删除操作代码的详细内容。更多信息请关注PHP中文网其他相关文章！
本站声明
本文内容由网友自发贡献，版权归原作者所有，本站不承担相应法律责任。如您发现有涉嫌抄袭侵权的内容，请联系admin@php.cn
热AI工具
Undresser.AI Undress
人工智能驱动的应用程序，用于创建逼真的裸体照片
AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。
Undress AI Tool
免费脱衣服图片
Clothoff.io
AI脱衣机
Video Face Swap
使用我们完全免费的人工智能换脸工具轻松在任何视频中换脸！
热门文章
刺客信条阴影：贝壳谜语解决方案
3 周前
By DDD
Windows 11 KB5054979中的新功能以及如何解决更新问题
2 周前
By DDD
在哪里可以找到原子中的起重机控制钥匙卡
3 周前
By DDD
<🎜>：死铁路 - 如何完成所有挑战
4 周前
By DDD
Atomfall指南：项目位置，任务指南和技巧
4 周前
By DDD
热工具
记事本++7.3.1
好用且免费的代码编辑器
SublimeText3汉化版
中文版，非常好用
禅工作室 13.0.1
功能强大的PHP集成开发环境
Dreamweaver CS6
视觉化网页开发工具
SublimeText3 Mac版
神级代码编辑软件(SublimeText3)
热门话题
与MySQL中使用索引相比，全表扫描何时可以更快？
Apr 09, 2025 am 12:05 AM
全表扫描在MySQL中可能比使用索引更快，具体情况包括：1)数据量较小时；2)查询返回大量数据时；3)索引列不具备高选择性时；4)复杂查询时。通过分析查询计划、优化索引、避免过度索引和定期维护表，可以在实际应用中做出最优选择。
说明InnoDB全文搜索功能。
Apr 02, 2025 pm 06:09 PM
InnoDB的全文搜索功能非常强大，能够显着提高数据库查询效率和处理大量文本数据的能力。 1）InnoDB通过倒排索引实现全文搜索，支持基本和高级搜索查询。 2）使用MATCH和AGAINST关键字进行搜索，支持布尔模式和短语搜索。 3）优化方法包括使用分词技术、定期重建索引和调整缓存大小，以提升性能和准确性。
可以在 Windows 7 上安装 mysql 吗
Apr 08, 2025 pm 03:21 PM
是的，可以在 Windows 7 上安装 MySQL，虽然微软已停止支持 Windows 7，但 MySQL 仍兼容它。不过，安装过程中需要注意以下几点：下载适用于 Windows 的 MySQL 安装程序。选择合适的 MySQL 版本（社区版或企业版）。安装过程中选择适当的安装目录和字符集。设置 root 用户密码，并妥善保管。连接数据库进行测试。注意 Windows 7 上的兼容性问题和安全性问题，建议升级到受支持的操作系统。
mysql：简单的概念，用于轻松学习
Apr 10, 2025 am 09:29 AM
MySQL是一个开源的关系型数据库管理系统。1）创建数据库和表：使用CREATEDATABASE和CREATETABLE命令。2）基本操作：INSERT、UPDATE、DELETE和SELECT。3）高级操作：JOIN、子查询和事务处理。4）调试技巧：检查语法、数据类型和权限。5）优化建议：使用索引、避免SELECT*和使用事务。
InnoDB中的聚类索引和非簇索引（次级索引）之间的差异。
Apr 02, 2025 pm 06:25 PM
聚集索引和非聚集索引的区别在于：1.聚集索引将数据行存储在索引结构中，适合按主键查询和范围查询。2.非聚集索引存储索引键值和数据行的指针，适用于非主键列查询。
mysql 和 mariadb 可以共存吗
Apr 08, 2025 pm 02:27 PM
MySQL 和 MariaDB 可以共存，但需要谨慎配置。关键在于为每个数据库分配不同的端口号和数据目录，并调整内存分配和缓存大小等参数。连接池、应用程序配置和版本差异也需要考虑，需要仔细测试和规划以避免陷阱。在资源有限的情况下，同时运行两个数据库可能会导致性能问题。
mysql用户和数据库的关系
Apr 08, 2025 pm 07:15 PM
MySQL 数据库中，用户和数据库的关系通过权限和表定义。用户拥有用户名和密码，用于访问数据库。权限通过 GRANT 命令授予，而表由 CREATE TABLE 命令创建。要建立用户和数据库之间的关系，需创建数据库、创建用户，然后授予权限。
说明不同类型的MySQL索引（B树，哈希，全文，空间）。
Apr 02, 2025 pm 07:05 PM
MySQL支持四种索引类型：B-Tree、Hash、Full-text和Spatial。1.B-Tree索引适用于等值查找、范围查询和排序。2.Hash索引适用于等值查找，但不支持范围查询和排序。3.Full-text索引用于全文搜索，适合处理大量文本数据。4.Spatial索引用于地理空间数据查询，适用于GIS应用。
