区别和联系:AIC与bBIC

AIC(Akaike Information Criterion)和BIC(Bayesian Information Criterion)是常用的模型选择标准,用于比较不同模型并选择最适合数据的模型。这两个标准的目标都是在模型的拟合优度和复杂性之间寻求平衡,以避免过拟合或欠拟合问题。 AIC是由赤池弘次(Hirotugu Akaike)提出的,它基于信息论的概念,考虑了模型的拟合优度和参数数量之间的平衡。AIC的计算公式为AIC = -2log(L) + 2k,其中L表示模型的最大似然估计值,k表示模型的参数数量。 BIC是由斯瓦齐亚克(Gideon E. Schwarz)提出的,它是基于贝叶斯
AIC和BIC是用于权衡模型适应度和复杂性的指标,可适用于各种统计模型,包括聚类方法。然而,由于聚类方法的类型和对数据分布的假设不同,AIC和BIC的具体形式可能会有所不同。
AIC和BIC之间的主要区别在于它们如何权衡拟合优度和复杂性之间的权衡。
AIC基于最大似然原理,它会惩罚相对于数据大小具有大量参数的模型。
AIC的公式
AIC=2k-2ln(L)
目标是找到具有最低AIC值的模型,以平衡拟合优度和复杂性。其中k是模型参数数量,即模型L的最大似然。
BIC与AIC类似,但它对参数数量较多的模型的惩罚更为严重。
BIC的公式
BIC=kln(n)-2ln(L)
其中k是模型中参数的n数量,是数据点的数量,L是模型的最大似然。目标是找到具有最低BIC值的模型,因为这表明该模型具有拟合优度和复杂性的最佳平衡。
一般来说,BIC会比AIC更严厉地惩罚具有大量参数的模型,因此当目标是找到一个更加简约模型时,可以使用BIC。
在模型选择的上下文中,简约模型是具有少量参数但仍能很好地拟合数据的模型。简约模型的目标是简化模型并降低复杂性,同时仍然捕获数据的基本特征。当提供相似水平的准确度时,简约模型比更复杂的模型更受欢迎,因为它更容易解释,不太容易过度拟合,并且计算效率更高。
还需要注意的是AIC和BIC都可用于比较不同的模型并为给定数据集选择最佳模型。
以上是区别和联系:AIC与bBIC的详细内容。更多信息请关注PHP中文网其他相关文章!

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

Video Face Swap
使用我们完全免费的人工智能换脸工具轻松在任何视频中换脸!

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)
 字节跳动剪映推出 SVIP 超级会员:连续包年 499 元,提供多种 AI 功能
Jun 28, 2024 am 03:51 AM
字节跳动剪映推出 SVIP 超级会员:连续包年 499 元,提供多种 AI 功能
Jun 28, 2024 am 03:51 AM
本站6月27日消息,剪映是由字节跳动旗下脸萌科技开发的一款视频剪辑软件,依托于抖音平台且基本面向该平台用户制作短视频内容,并兼容iOS、安卓、Windows、MacOS等操作系统。剪映官方宣布会员体系升级,推出全新SVIP,包含多种AI黑科技,例如智能翻译、智能划重点、智能包装、数字人合成等。价格方面,剪映SVIP月费79元,年费599元(本站注:折合每月49.9元),连续包月则为59元每月,连续包年为499元每年(折合每月41.6元)。此外,剪映官方还表示,为提升用户体验,向已订阅了原版VIP
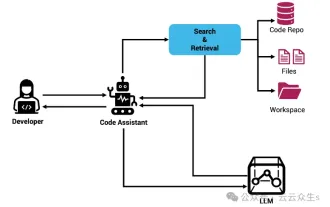 使用Rag和Sem-Rag提供上下文增强AI编码助手
Jun 10, 2024 am 11:08 AM
使用Rag和Sem-Rag提供上下文增强AI编码助手
Jun 10, 2024 am 11:08 AM
通过将检索增强生成和语义记忆纳入AI编码助手,提升开发人员的生产力、效率和准确性。译自EnhancingAICodingAssistantswithContextUsingRAGandSEM-RAG,作者JanakiramMSV。虽然基本AI编程助手自然有帮助,但由于依赖对软件语言和编写软件最常见模式的总体理解,因此常常无法提供最相关和正确的代码建议。这些编码助手生成的代码适合解决他们负责解决的问题,但通常不符合各个团队的编码标准、惯例和风格。这通常会导致需要修改或完善其建议,以便将代码接受到应
 七个很酷的GenAI & LLM技术性面试问题
Jun 07, 2024 am 10:06 AM
七个很酷的GenAI & LLM技术性面试问题
Jun 07, 2024 am 10:06 AM
想了解更多AIGC的内容,请访问:51CTOAI.x社区https://www.51cto.com/aigc/译者|晶颜审校|重楼不同于互联网上随处可见的传统问题库,这些问题需要跳出常规思维。大语言模型(LLM)在数据科学、生成式人工智能(GenAI)和人工智能领域越来越重要。这些复杂的算法提升了人类的技能,并在诸多行业中推动了效率和创新性的提升,成为企业保持竞争力的关键。LLM的应用范围非常广泛,它可以用于自然语言处理、文本生成、语音识别和推荐系统等领域。通过学习大量的数据,LLM能够生成文本
 微调真的能让LLM学到新东西吗:引入新知识可能让模型产生更多的幻觉
Jun 11, 2024 pm 03:57 PM
微调真的能让LLM学到新东西吗:引入新知识可能让模型产生更多的幻觉
Jun 11, 2024 pm 03:57 PM
大型语言模型(LLM)是在巨大的文本数据库上训练的,在那里它们获得了大量的实际知识。这些知识嵌入到它们的参数中,然后可以在需要时使用。这些模型的知识在训练结束时被“具体化”。在预训练结束时,模型实际上停止学习。对模型进行对齐或进行指令调优,让模型学习如何充分利用这些知识,以及如何更自然地响应用户的问题。但是有时模型知识是不够的,尽管模型可以通过RAG访问外部内容,但通过微调使用模型适应新的领域被认为是有益的。这种微调是使用人工标注者或其他llm创建的输入进行的,模型会遇到额外的实际知识并将其整合
 你所不知道的机器学习五大学派
Jun 05, 2024 pm 08:51 PM
你所不知道的机器学习五大学派
Jun 05, 2024 pm 08:51 PM
机器学习是人工智能的重要分支,它赋予计算机从数据中学习的能力,并能够在无需明确编程的情况下改进自身能力。机器学习在各个领域都有着广泛的应用,从图像识别和自然语言处理到推荐系统和欺诈检测,它正在改变我们的生活方式。机器学习领域存在着多种不同的方法和理论,其中最具影响力的五种方法被称为“机器学习五大派”。这五大派分别为符号派、联结派、进化派、贝叶斯派和类推学派。1.符号学派符号学(Symbolism),又称为符号主义,强调利用符号进行逻辑推理和表达知识。该学派认为学习是一种逆向演绎的过程,通过已有的
 为大模型提供全新科学复杂问答基准与测评体系,UNSW、阿贡、芝加哥大学等多家机构联合推出SciQAG框架
Jul 25, 2024 am 06:42 AM
为大模型提供全新科学复杂问答基准与测评体系,UNSW、阿贡、芝加哥大学等多家机构联合推出SciQAG框架
Jul 25, 2024 am 06:42 AM
编辑|ScienceAI问答(QA)数据集在推动自然语言处理(NLP)研究发挥着至关重要的作用。高质量QA数据集不仅可以用于微调模型,也可以有效评估大语言模型(LLM)的能力,尤其是针对科学知识的理解和推理能力。尽管当前已有许多科学QA数据集,涵盖了医学、化学、生物等领域,但这些数据集仍存在一些不足。其一,数据形式较为单一,大多数为多项选择题(multiple-choicequestions),它们易于进行评估,但限制了模型的答案选择范围,无法充分测试模型的科学问题解答能力。相比之下,开放式问答
 SOTA性能,厦大多模态蛋白质-配体亲和力预测AI方法,首次结合分子表面信息
Jul 17, 2024 pm 06:37 PM
SOTA性能,厦大多模态蛋白质-配体亲和力预测AI方法,首次结合分子表面信息
Jul 17, 2024 pm 06:37 PM
编辑|KX在药物研发领域,准确有效地预测蛋白质与配体的结合亲和力对于药物筛选和优化至关重要。然而,目前的研究没有考虑到分子表面信息在蛋白质-配体相互作用中的重要作用。基于此,来自厦门大学的研究人员提出了一种新颖的多模态特征提取(MFE)框架,该框架首次结合了蛋白质表面、3D结构和序列的信息,并使用交叉注意机制进行不同模态之间的特征对齐。实验结果表明,该方法在预测蛋白质-配体结合亲和力方面取得了最先进的性能。此外,消融研究证明了该框架内蛋白质表面信息和多模态特征对齐的有效性和必要性。相关研究以「S
 SK 海力士 8 月 6 日将展示 AI 相关新品:12 层 HBM3E、321-high NAND 等
Aug 01, 2024 pm 09:40 PM
SK 海力士 8 月 6 日将展示 AI 相关新品:12 层 HBM3E、321-high NAND 等
Aug 01, 2024 pm 09:40 PM
本站8月1日消息,SK海力士今天(8月1日)发布博文,宣布将出席8月6日至8日,在美国加利福尼亚州圣克拉拉举行的全球半导体存储器峰会FMS2024,展示诸多新一代产品。未来存储器和存储峰会(FutureMemoryandStorage)简介前身是主要面向NAND供应商的闪存峰会(FlashMemorySummit),在人工智能技术日益受到关注的背景下,今年重新命名为未来存储器和存储峰会(FutureMemoryandStorage),以邀请DRAM和存储供应商等更多参与者。新产品SK海力士去年在






