编辑 | XS
Nature 在 2023 年 11 月发表了两项重要研究成果：蛋白质合成技术 Chroma 和晶体材料设计方法 GNoME。这两项研究都采用了图神经网络作为处理科学数据的工具。
实际上，图神经网络，特别是几何图神经网络，一直是科学智能（AI for Science）研究的重要工具。这是因为，科学领域中的粒子、分子、蛋白质、晶体等物理系统均可被建模成一种特殊的数据结构——几何图。
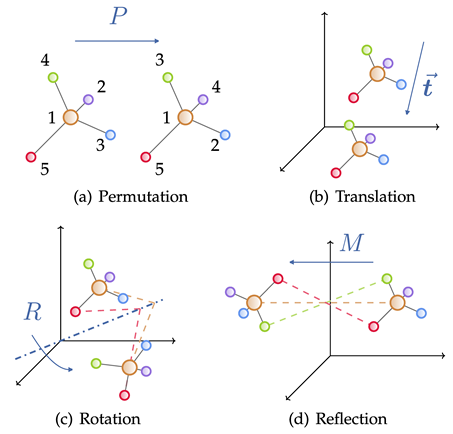
与一般的拓扑图不同，为了更好描述物理系统，几何图加入了不可或缺的空间信息，需要满足平移、旋转和翻转的物理对称性。鉴于几何图神经网络对于物理系统建模的优越性，近年来各类方法层出不穷，论文数量持续增长。
近日，人大高瓴联合腾讯 AI Lab、清华、斯坦福等机构发布综述论文：《A Survey of Geometric Graph Neural Networks: Data Structures, Models and Applications》。该综述在简要介绍群论、对称性等理论知识的基础上，从数据结构、模型到众多科学应用，对相关几何图神经网络文献进行了系统的梳理。
论文链接：https://arxiv.org/abs/2403.00485
GitHub链接：https://github.com/RUC-GLAD/GGNN4Science
在这篇综述中，作者调研了 300 多篇参考文献，归纳出 3 种不同的几何图神经网络模型，介绍了面向粒子、分子、蛋白质等多种科学数据上共 23 种不同任务的相关方法，收集了 50 多个相关评测数据集。最后，综述展望了未来的研究方向，包括几何图基础模型、与大语言模型结合等。
下面是各章节简要介绍。
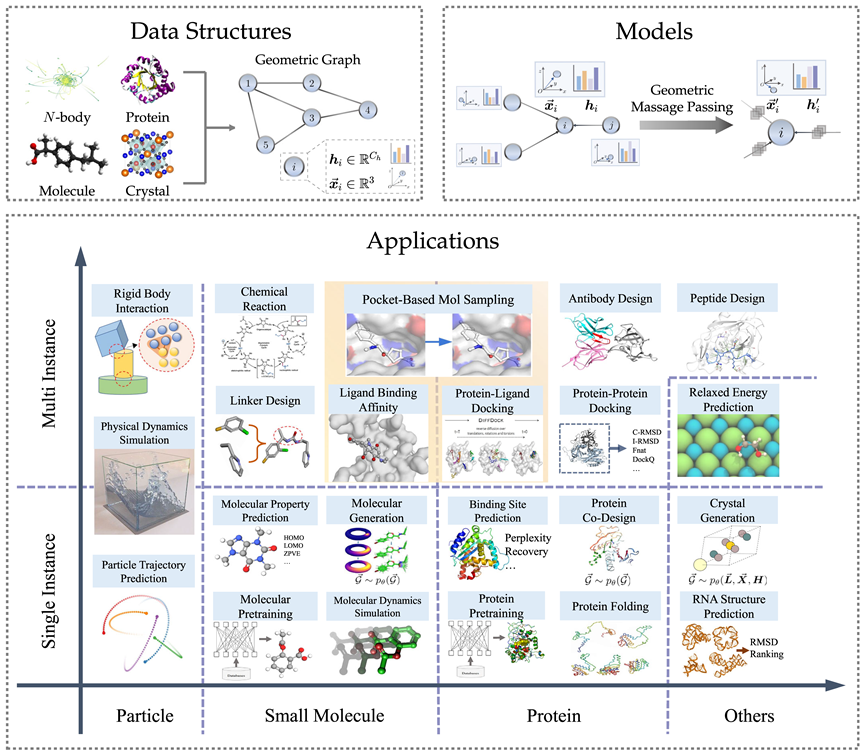
几何图数据结构
几何图由邻接矩阵、节点特征、节点几何信息（例如坐标）构成。在欧氏空间中，几何图通常表现出平移、旋转和反射的物理对称性，一般使用群来刻画这些变换，包括欧式群、平移群、正交群、置换群等等。直观上看，可以理解为置换、平移、旋转、翻转四种操作按一定顺序的复合。
对于众多 AI for Science 领域，几何图是一种有力且通用的表示方法，其可以用于表示众多物理系统，包括小分子、蛋白质、晶体、物理点云等。
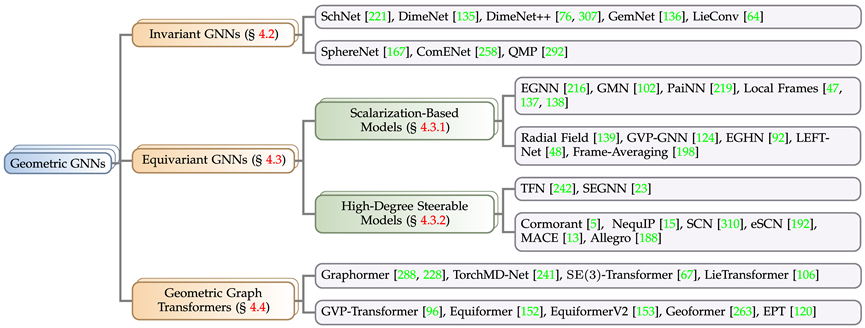
几何图神经网络模型
根据实际问题中的求解目标对于对称性的要求，本文将几何图神经网络分为三类：不变（invariant）模型、等变（equivariant）模型、以及受 Transformer 架构启发的 Geometric Graph Transformer，其中等变模型又细分为标量化方法模型（Scalarization-Based Model）与基于球面调和的高阶可操控模型（High-Degree Steerable Model）。按照上述规则，文章收集并归类了近年来知名的几何图神经网络模型。
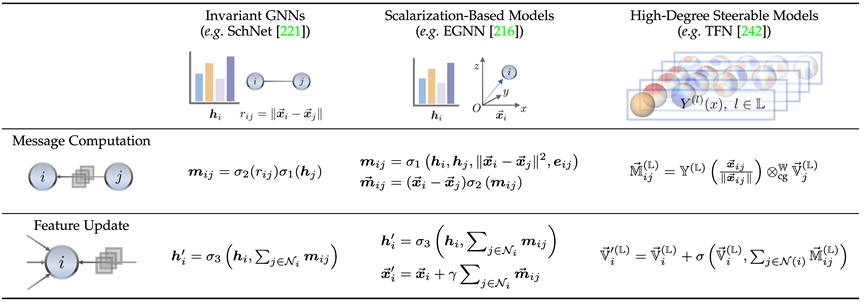
这里我们通过各个分支的代表性工作简要介绍不变模型（SchNet[1]）、标量化方法模型（EGNN[2]）、高阶可操控模型（TFN[3]）的关联与区别。可以发现三者均是采用了消息传递机制，只是身为等变模型的后两者额外引入了一次几何消息传递。
不变模型主要利用节点本身的特征（如原子种类、质量、带电量等）与原子间的不变特征（如距离、角度[4]、二面角[5]）等进行消息计算，随后进行传播。
而在此之上，标量化方法额外通过节点间坐标差引入了几何信息，并将不变信息作为几何信息的权重进行线性组合，实现了等变性的引入。
高阶可操控模型则是使用了高阶的球面调和（Spherical Harmonics）与 Wigner-D 矩阵表征系统的几何信息，这类方法通过量子力学中的 Clebsch–Gordan 系数操控不可约表示的阶数，从而实现几何消息传递过程。
几何图神经网络通过这类设计保证的对称性，准确率有大幅提升，并且在生成任务中也大放异彩。
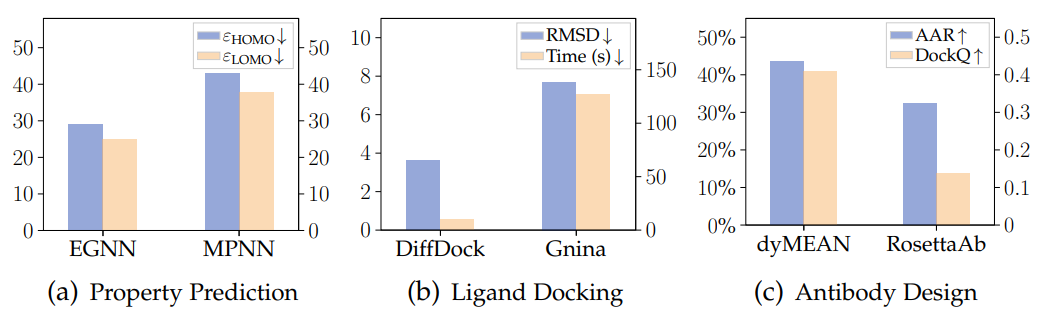
下图是几何图神经网络与传统模型在 QM9、PDBBind、SabDab 三个数据集上进行分子性质预测、蛋白质-配体对接和抗体设计（生成）三个任务中的结果，可以明显看出几何图神经网络的优势。
科学应用
在科学应用方面，综述涵盖了物理（粒子）、生物化学（小分子、蛋白质）以及其它如晶体等多个应用场景，任务定义与所需保证对称性种类出发，分别介绍了各个任务中的常用数据集与该类任务中的经典模型设计思路。
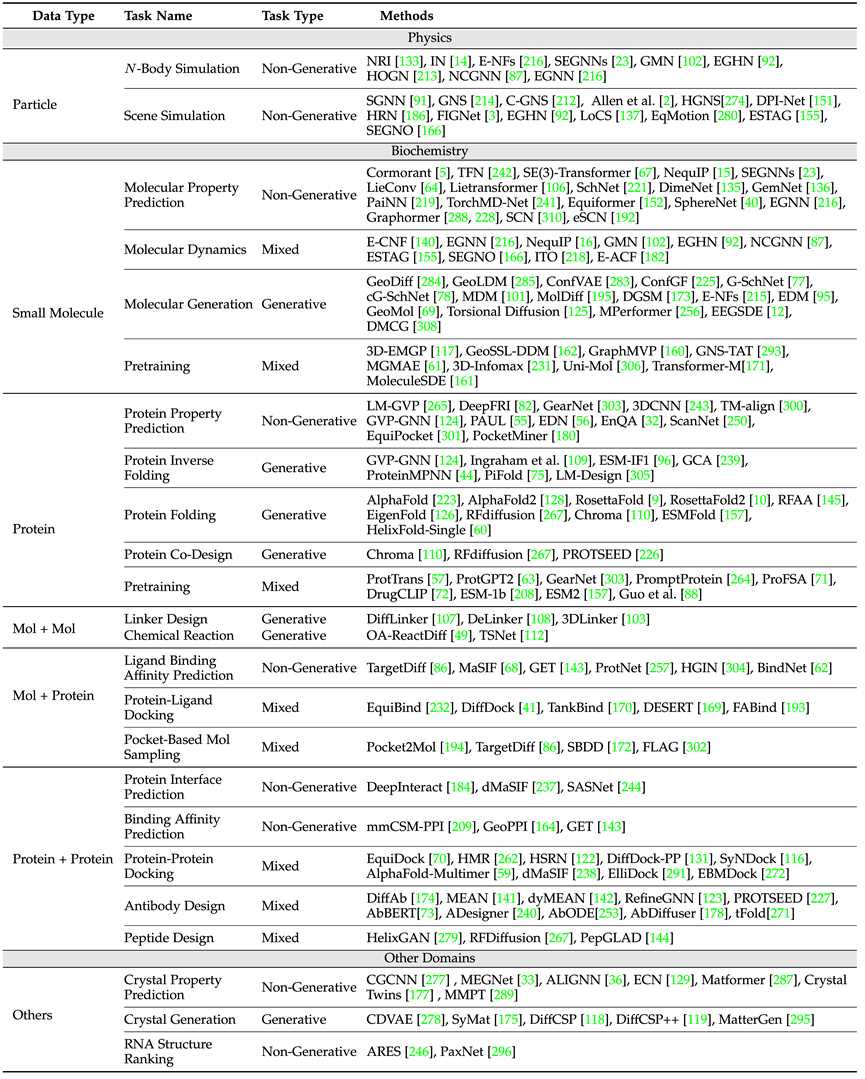
上表展示了各个领域的常见任务与经典模型，其中，按照单一实例与多实例（如化学反应，需要多分子共同参与），文章单独区分了小分子-小分子、小分子-蛋白质、蛋白质-蛋白质三个领域。
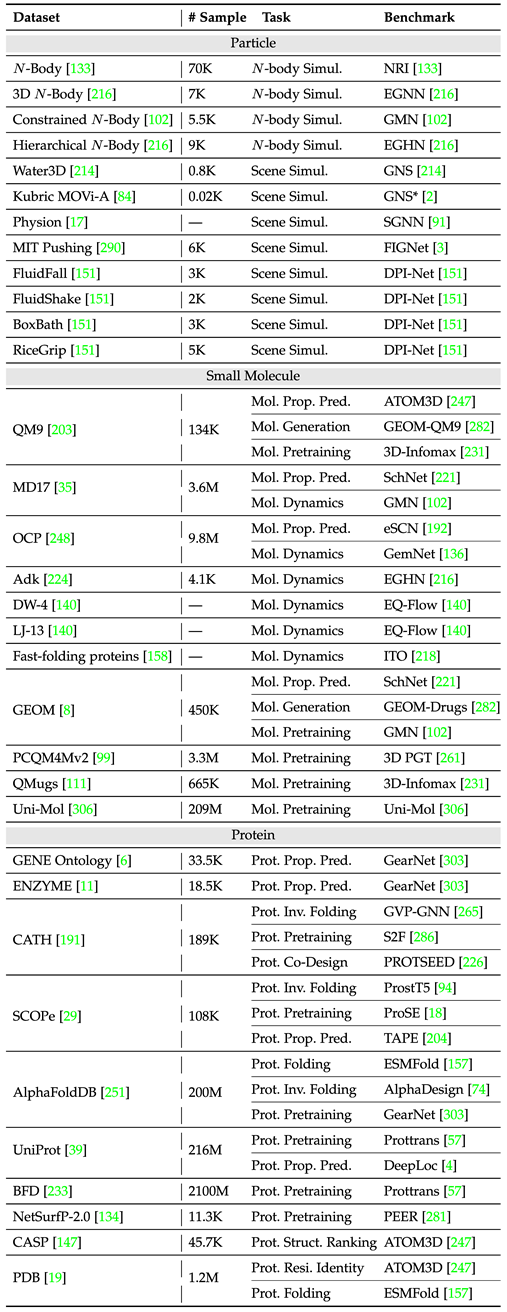
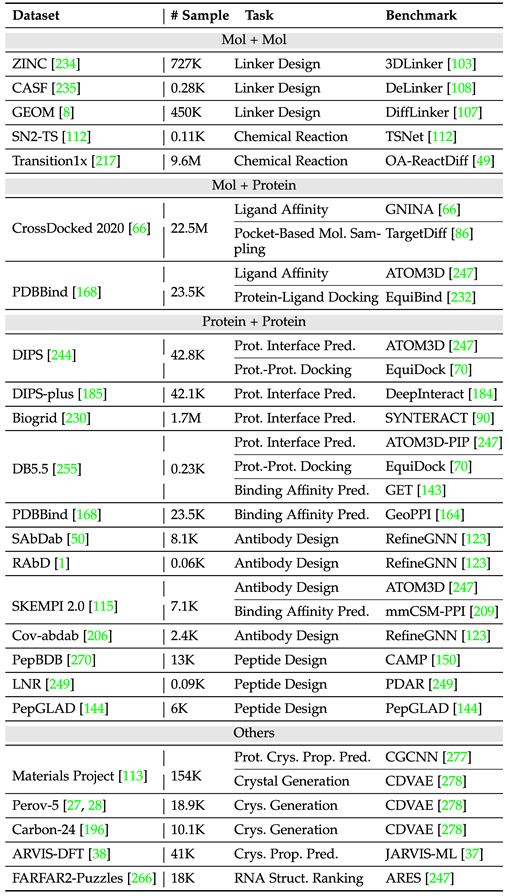
为了更好地方便领域内进行模型设计与实验开展，文章按照单一实例与多实例统计了两类任务的常用数据集与基准（benchmark），并记录了不同数据集的样本量与任务种类。
下表整理了常见的单实例任务数据集。
下表整理了常见的多实例任务数据集。
未来展望
文章就几个方面进行了初步的展望，希望能作抛砖引玉之用：
1. 几何图基础模型
在各种任务和领域中采用统一的基础模型的优越性在GPT系列模型的显著进步中已经体现得淋漓尽致。如何在任务空间、数据空间、模型空间进行合理的设计，从而将这种思路引入到针对几何图神经网络的设计上仍是一个有趣的开放问题。
2. 模型训练与现实世界实验验证的高效循环
科学数据的获取是昂贵且耗时的，而仅仅在独立数据集上评估的模型不能直接反应来自现实世界的反馈。如何类似于GNoME（集成了一个端到端的流水线，包括图网络训练、密度泛函理论计算和用于材料发现和合成的自动实验室）实现高效的模型-现实循环迭代的实验范式的重要性将会与日俱增。
3. 与大型语言模型（LLMs）的融合
大型语言模型（LLMs）已被广泛证明具有丰富的知识，涵盖了各个领域。虽然已经有一些工作利用 LLMs 进行某些任务，例如分子属性预测和药物设计，但它们仅在基元或分子图上操作。如何将它们与几何图神经网络有机组合，使其能够处理 3D 结构信息并在 3D 结构上执行预测或生成，仍然具有相当的挑战性。
4. 等变性约束条件的放松
毫无疑问，等变性对增强数据效率和模型泛化能力至关重要，但值得注意的是，过强等变性约束有时可能过于限制模型，潜在地损害其性能。因此，如何使得所设计的模型在等变性与适应能力中取得平衡是一个非常有趣的问题。这方面的探索不仅可以丰富我们对模型行为的理解，还可以为开发更具鲁棒性和通用性的解决方案铺平道路，使其具有更广泛的适用性。
参考文献
[1] Schütt K, Kindermans P J, Sauceda Felix H E, et al. Schnet: A continuous-filter convolutional neural network for modeling quantum interactions[J]. Advances in neural information processing systems, 2017, 30.
[2] Satorras VG, Hoogeboom E, Welling M. E (n)等变图神经网络[C]//机器学习国际会议。 PMLR，2021：9323-9332。
[3] Thomas N、Smidt T、Kearnes S 等人。张量场网络：3d 点云的旋转和平移等变神经网络[J]. arXiv 预印本 arXiv:1802.08219, 2018.
[4] Gasteiger J, Groß J, Günnemann S. 分子图的定向消息传递[C]//学习表示国际会议。 2019.
[5] Gasteiger J, Becker F, Günnemann S. Gemnet：分子的通用有向图神经网络[J].神经信息处理系统的进展，2021, 34: 6790-6802.
[6] Merchant A, Batzner S, Schoenholz S S, et al.扩展深度学习以促进材料发现[J].自然, 2023, 624(7990): 80-85.
以上是AI4Science的基石：几何图神经网络，最全综述来了！人大高瓴联合腾讯AI lab、清华、斯坦福等发布的详细内容。更多信息请关注PHP中文网其他相关文章！
