CUDA之通用矩阵乘法：从入门到熟练！

通用矩阵乘法（General Matrix Multiplication，GEMM）是许多应用程序和算法中至关重要的一部分，也是评估计算机硬件性能的重要指标之一。通过深入研究和优化GEMM的实现，可以帮助我们更好地理解高性能计算以及软硬件系统之间的关系。在计算机科学中，对GEMM进行有效的优化可以提高计算速度并节省资源，这对于提高计算机系统的整体性能至关重要。深入了解GEMM的工作原理和优化方法，有助于我们更好地利用现代计算硬件的潜力，并为各种复杂计算任务提供更高效的解决方案。通过对GEMM性能的优化和改进，可以加

一、GEMM的基本特征

1.1 GEMM计算过程及复杂度

GEMM 的定义为：

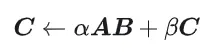
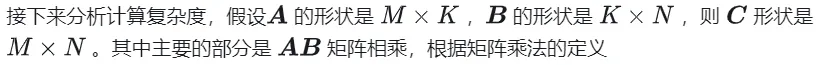
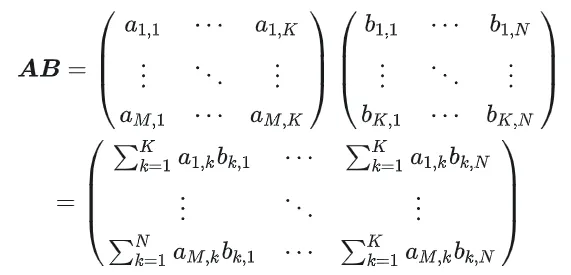
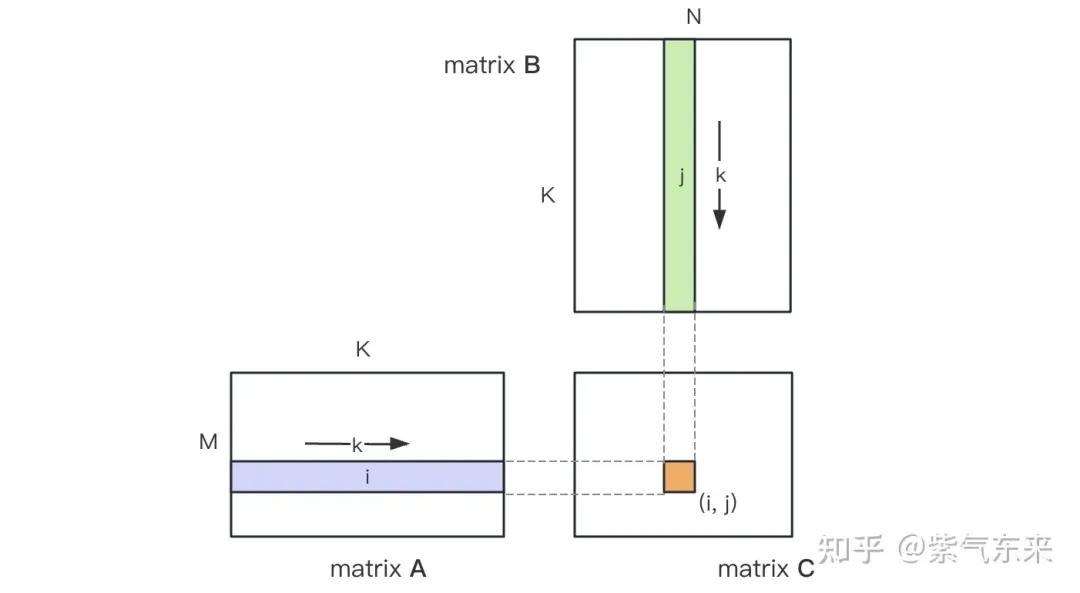
矩阵乘法的计算示意

1.2 简单实现及过程分析

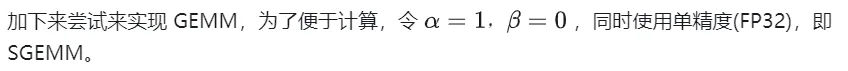
下面是按照原始定义实现的 CPU 上实现的代码，之后用以作为精度的对照

#define OFFSET(row, col, ld) ((row) * (ld) + (col))void cpuSgemm(float *a, float *b, float *c, const int M, const int N, const int K) {for (int m = 0; m 

下面使用CUDA实现最简单的矩阵乘法的Kernal，一共使用 M * N 个线程完成整个矩阵乘法。每个线程负责矩阵C中一个元素的计算，需要完成K次乘累加。矩阵A,B,C均存放与全局内存中（由修饰符 __global__ 确定），完整代码见 sgemm_naive.cu 。

__global__ void naiveSgemm(float * __restrict__ a, float * __restrict__ b, float * __restrict__ c,const int M, const int N, const int K) {int n = blockIdx.x * blockDim.x + threadIdx.x;int m = blockIdx.y * blockDim.y + threadIdx.y;if (m 

编译完成，在Tesla V100-PCIE-32GB上执行的结果如下，根据V100的白皮书，FP32 的峰值算力为 15.7 TFLOPS，因此该方式算力利用率仅有11.5%。

M N K =128128 1024, Time = 0.00010083 0.00010260 0.00010874 s, AVG Performance = 304.5951 GflopsM N K =192192 1024, Time = 0.00010173 0.00010198 0.00010253 s, AVG Performance = 689.4680 GflopsM N K =256256 1024, Time = 0.00010266 0.00010318 0.00010384 s, AVG Performance =1211.4281 GflopsM N K =384384 1024, Time = 0.00019475 0.00019535 0.00019594 s, AVG Performance =1439.7206 GflopsM N K =512512 1024, Time = 0.00037693 0.00037794 0.00037850 s, AVG Performance =1322.9753 GflopsM N K =768768 1024, Time = 0.00075238 0.00075558 0.00075776 s, AVG Performance =1488.9271 GflopsM N K = 1024 1024 1024, Time = 0.00121562 0.00121669 0.00121789 s, AVG Performance =1643.8068 GflopsM N K = 1536 1536 1024, Time = 0.00273072 0.00275611 0.00280208 s, AVG Performance =1632.7386 GflopsM N K = 2048 2048 1024, Time = 0.00487622 0.00488028 0.00488614 s, AVG Performance =1639.2518 GflopsM N K = 3072 3072 1024, Time = 0.01001603 0.01071136 0.01099990 s, AVG Performance =1680.4589 GflopsM N K = 4096 4096 1024, Time = 0.01771046 0.01792170 0.01803462 s, AVG Performance =1785.5450 GflopsM N K = 6144 6144 1024, Time = 0.03988969 0.03993405 0.04000595 s, AVG Performance =1802.9724 GflopsM N K = 8192 8192 1024, Time = 0.07119219 0.07139694 0.07160816 s, AVG Performance =1792.7940 GflopsM N K =1228812288 1024, Time = 0.15978026 0.15993242 0.16043369 s, AVG Performance =1800.7606 GflopsM N K =1638416384 1024, Time = 0.28559187 0.28567238 0.28573316 s, AVG Performance =1792.2629 Gflops

下面以M=512,K=512,N=512,为例，详细分析一下上述计算过程的workflow：

1. 在 Global Memory 中分别为矩阵A,B,C分配存储空间.
2. 由于矩阵C中每个元素的计算均相互独立, 因此在并行度映射中让每个thread 对应矩阵C中 1 个元素的计算.
3. 执行配置 (execution configuration)中 gridSize 和 blockSize 均有 x(列向)、y(行向)两个维度, 其中

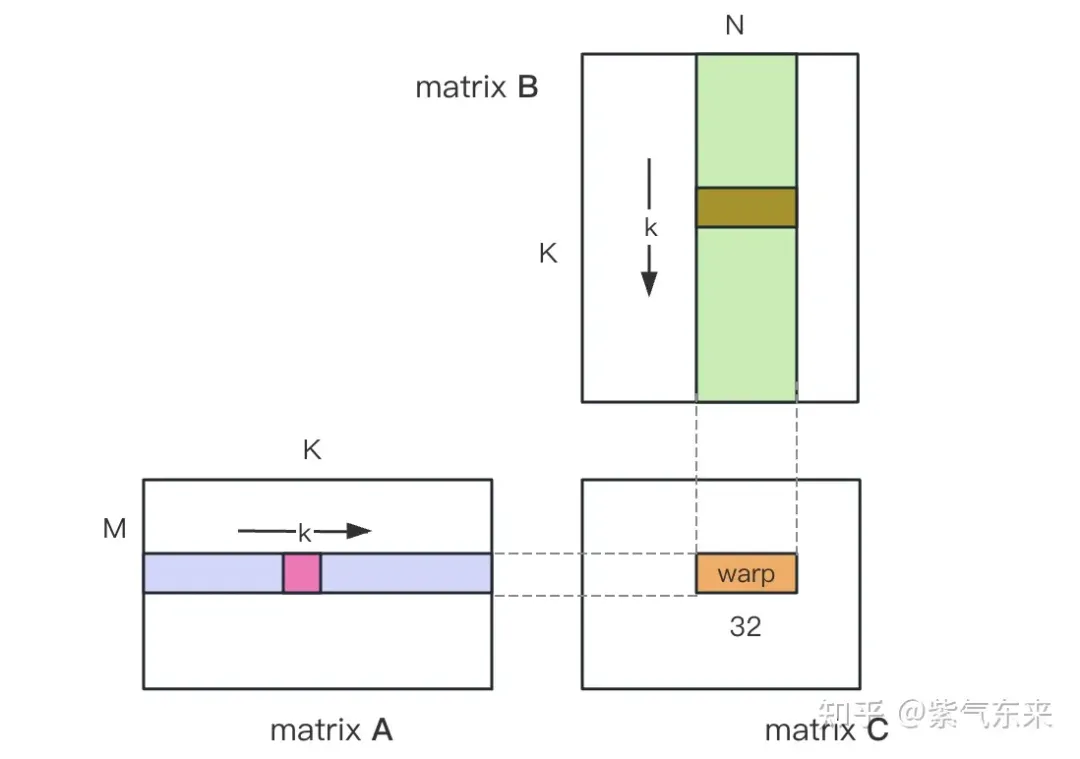
nsys 记录 的 naive 版本的 profiling

二、GEMM的优化探究

前文仅仅在功能上实现了 GEMM，性能上还远远不及预期，本节将主要研究 GEMM 性能上的优化。

2.1 矩阵分块利用Shared Memory

上述的计算需要两次Global Memory的load才能完成一次乘累加运算，计算访存比极低，没有有效的数据复用。所以可以用 Shared Memory 来减少重复的内存读取。

首先把矩阵C等分为BMxBN大小的分块，每个分块由一个 Block 计算，其中每个Thread负责计算矩阵C中的TMxTN个元素。之后计算所需的数据全部从 smem 中读取，就消除了一部分重复的A,B矩阵内存读取。考虑到 Shared Memory 容量有限，可以在K维上每次读取BK大小的分块，这样的循环一共需要K / BK次以完成整个矩阵乘法操作，即可得到 Block 的结果。其过程如下图所示：

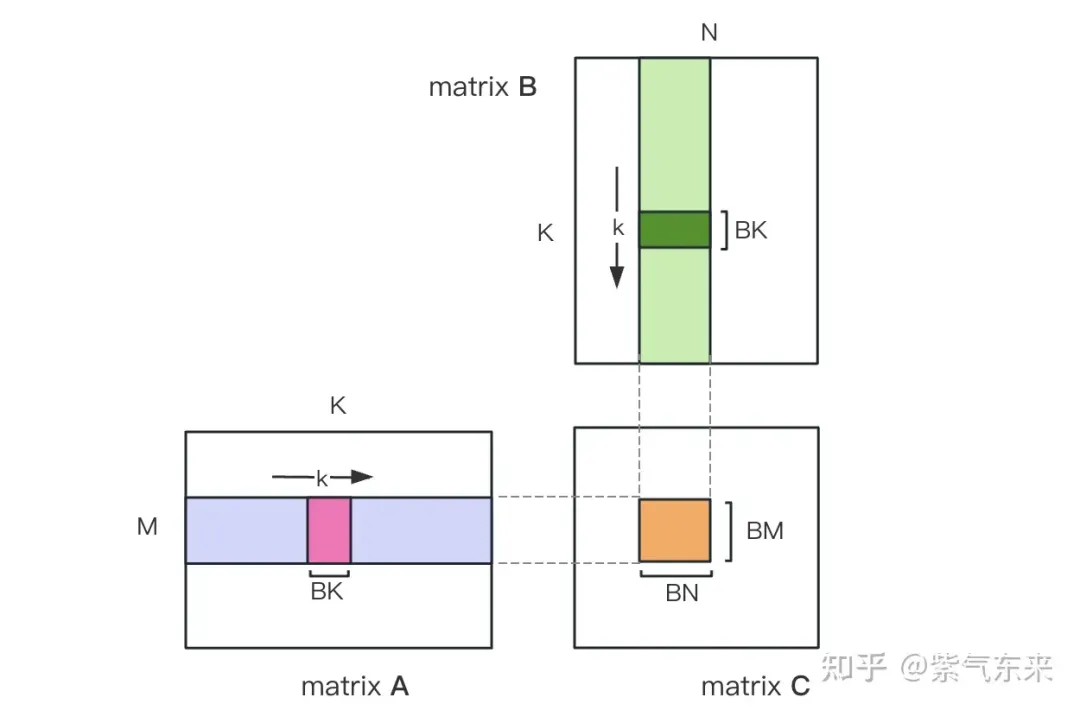
利用 Shared Memory 优化后，对每一个分块，可得：

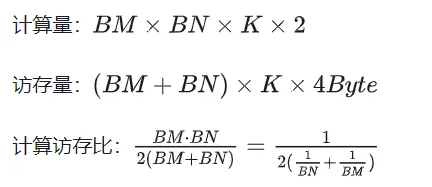
由上式可知BM和BN越大，计算访存比越高，性能就会越好。但是由于 Shared Memory 容量的限制(V100 1个SM仅96KB)，而一个Block需要占用 BK * (BM BN) * 4 Bytes大小。

TM和TN的取值也受到两方面限制，一方面是线程数的限制，一个Block中有BM / TM * BN / TN个线程，这个数字不能超过1024，且不能太高防止影响SM内Block间的并行；另一方面是寄存器数目的限制，一个线程至少需要TM * TN个寄存器用于存放矩阵C的部分和，再加上一些其它的寄存器，所有的寄存器数目不能超过256，且不能太高防止影响SM内同时并行的线程数目。

最终选取 BM = BN = 128，BK = 8，TM = TN = 8，则此时计算访存比为32。根据V100的理论算力15.7TFLOPS，可得 15.7TFLOPS/32 = 490GB/s，根据实测的HBM带宽为763GB/s，可知此时带宽不再会限制计算性能。

根据以上分析，kernel 函数实现过程如下，完整代码参见 sgemm_v1.cu，主要步骤包括：

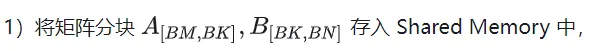
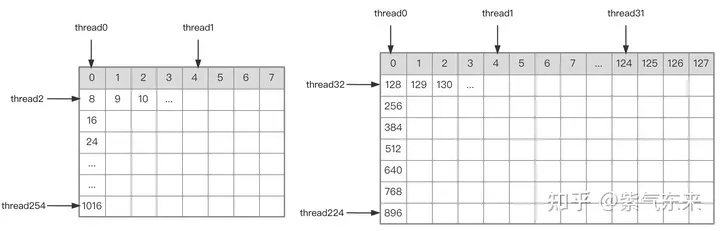
A B 矩阵分块的线程索引关系

确定好单个block的执行过程，接下来需要确定多block处理的不同分块在Global Memory中的对应关系，仍然以A为例进行说明。由于分块沿着行的方向移动，那么首先需要确定行号，根据 Grid 的二维全局线性索引关系，by * BM 表示该分块的起始行号，同时我们已知load_a_smem_m 为分块内部的行号，因此全局的行号为load_a_gmem_m = by * BM + load_a_smem_m 。由于分块沿着行的方向移动，因此列是变化的，需要在循环内部计算，同样也是先计算起始列号bk * BK 加速分块内部列号load_a_smem_k 得到 load_a_gmem_k = bk * BK + load_a_smem_k ，由此我们便可以确定了分块在原始数据中的位置OFFSET(load_a_gmem_m, load_a_gmem_k, K) 。同理可分析矩阵分块 的情况，不再赘述。

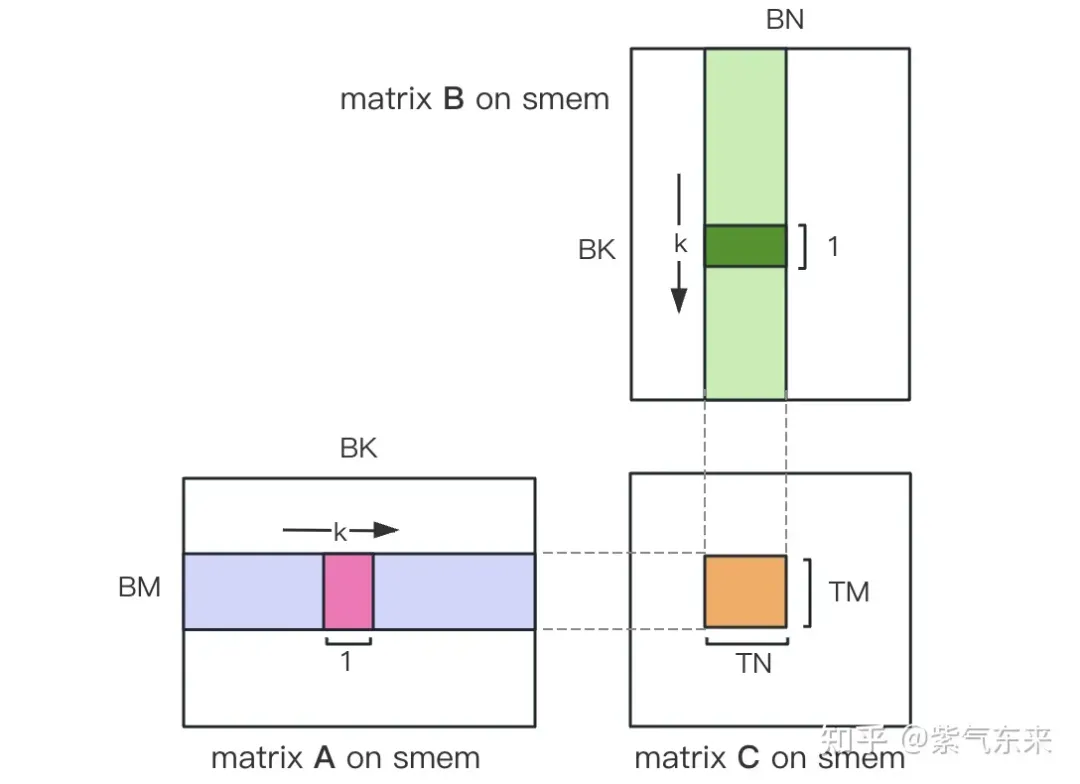
计算完后，还需要将其存入 Global Memory 中，这就需要计算其在 Global Memory 中的对应关系。由于存在更小的分块，则行和列均由3部分构成：全局行号store_c_gmem_m 等于大分块的起始行号by * BM+小分块的起始行号ty * TM+小分块内部的相对行号 i 。列同理。

__global__ void sgemm_V1(float * __restrict__ a, float * __restrict__ b, float * __restrict__ c,const int M, const int N, const int K) {const int BM = 128;const int BN = 128;const int BK = 8;const int TM = 8;const int TN = 8;const int bx = blockIdx.x;const int by = blockIdx.y;const int tx = threadIdx.x;const int ty = threadIdx.y;const int tid = ty * blockDim.x + tx;__shared__ float s_a[BM][BK];__shared__ float s_b[BK][BN];float r_c[TM][TN] = {0.0};int load_a_smem_m = tid >> 1;// tid/2, row of s_aint load_a_smem_k = (tid & 1) > 5; // tid/32, row of s_bint load_b_smem_n = (tid & 31) 

计算结果如下，性能达到了理论峰值性能的51.7%：

M N K =128128 1024, Time = 0.00031578 0.00031727 0.00032288 s, AVG Performance =98.4974 GflopsM N K =192192 1024, Time = 0.00031638 0.00031720 0.00031754 s, AVG Performance = 221.6661 GflopsM N K =256256 1024, Time = 0.00031488 0.00031532 0.00031606 s, AVG Performance = 396.4287 GflopsM N K =384384 1024, Time = 0.00031686 0.00031814 0.00032080 s, AVG Performance = 884.0425 GflopsM N K =512512 1024, Time = 0.00031814 0.00032007 0.00032493 s, AVG Performance =1562.1563 GflopsM N K =768768 1024, Time = 0.00032397 0.00034419 0.00034848 s, AVG Performance =3268.5245 GflopsM N K = 1024 1024 1024, Time = 0.00034570 0.00034792 0.00035331 s, AVG Performance =5748.3952 GflopsM N K = 1536 1536 1024, Time = 0.00068797 0.00068983 0.00069094 s, AVG Performance =6523.3424 GflopsM N K = 2048 2048 1024, Time = 0.00136173 0.00136552 0.00136899 s, AVG Performance =5858.5604 GflopsM N K = 3072 3072 1024, Time = 0.00271910 0.00273115 0.00274006 s, AVG Performance =6590.6331 GflopsM N K = 4096 4096 1024, Time = 0.00443805 0.00445964 0.00446883 s, AVG Performance =7175.4698 GflopsM N K = 6144 6144 1024, Time = 0.00917891 0.00950608 0.00996963 s, AVG Performance =7574.0999 GflopsM N K = 8192 8192 1024, Time = 0.01628838 0.01645271 0.01660790 s, AVG Performance =7779.8733 GflopsM N K =1228812288 1024, Time = 0.03592557 0.03597434 0.03614323 s, AVG Performance =8005.7066 GflopsM N K =1638416384 1024, Time = 0.06304122 0.06306373 0.06309302 s, AVG Performance =8118.7715 Gflops

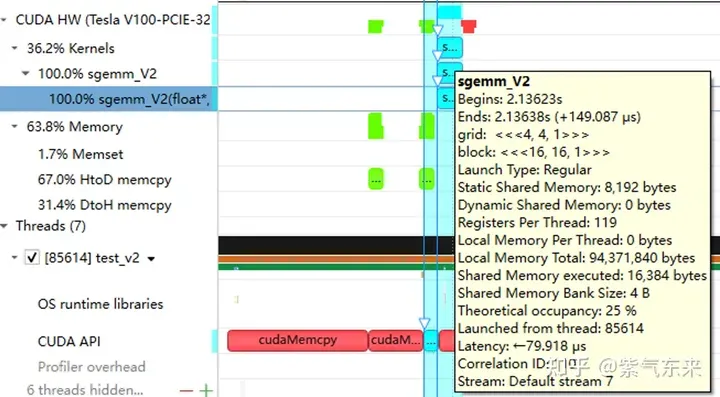
下面仍以M=512,K=512,N=512为例，分析一下结果。首先通过 profiling 可以看到 Shared Memory 占用为 8192 bytes，这与理论上(128+128)X8X4完全一致。

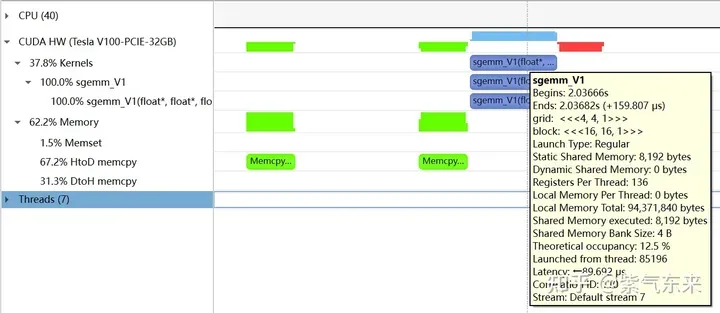nsys 记录 的 V1 版本的 profiling

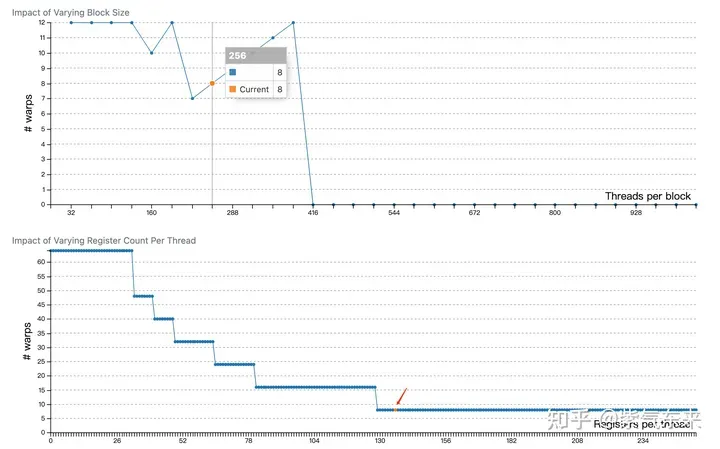
profiling 显示 Occupancy 为 12.5%，可以通过 cuda-calculator 加以印证，该例中 threads per block = 256, Registers per thread = 136, 由此可以计算得到每个SM中活跃的 warp 为8，而对于V100，每个SM中的 warp 总数为64，因此 Occupancy 为 8/64 = 12.5%。

2.2 解决 Bank Conflict 问题

上节通过利用 Shared Memory 大幅提高了访存效率，进而提高了性能，本节将进一步优化 Shared Memory 的使用。

Shared Memory一共划分为32个Bank，每个Bank的宽度为4 Bytes，如果需要访问同一个Bank的多个数据，就会发生Bank Conflict。例如一个Warp的32个线程，如果访问的地址分别为0、4、8、...、124，就不会发生Bank Conflict，只占用Shared Memory一拍的时间；如果访问的地址为0、8、16、...、248，这样一来地址0和地址128对应的数据位于同一Bank、地址4和地址132对应的数据位于同一Bank，以此类推，那么就需要占用Shared Memory两拍的时间才能读出。

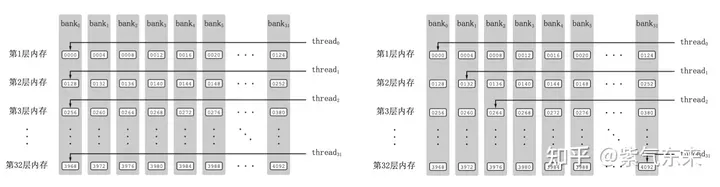
有 Bank Conflict VS 无 Bank Conflict

再看 V1 版本计算部分的三层循环，每次从Shared memory中取矩阵A的长度为TM的向量和矩阵B的长度为TN的向量，这两个向量做外积并累加到部分和中，一次外积共TM * TN次乘累加，一共需要循环BK次取数和外积。

接下来分析从Shared Memory load的过程中存在的Bank Conflict：

i) 取矩阵A需要取一个列向量，而矩阵A在Shared Memory中是按行存储的；

ii) 在TM = TN = 8的情况下，无论矩阵A还是矩阵B，从Shared Memory中取数时需要取连续的8个数，即便用LDS.128指令一条指令取四个数，也需要两条指令，由于一个线程的两条load指令的地址是连续的，那么同一个Warp不同线程的同一条load指令的访存地址就是被间隔开的，便存在着 Bank Conflict。

为了解决上述的两点Shared Memory的Bank Conflict，采用了一下两点优化：

i) 为矩阵A分配Shared Memory时形状分配为[BK][BM]，即让矩阵A在Shared Memory中按列存储

ii) 将原本每个线程负责计算的TM * TN的矩阵C，划分为下图中这样的两块TM/2 * TN的矩阵C，由于TM/2=4，一条指令即可完成A的一块的load操作，两个load可同时进行。

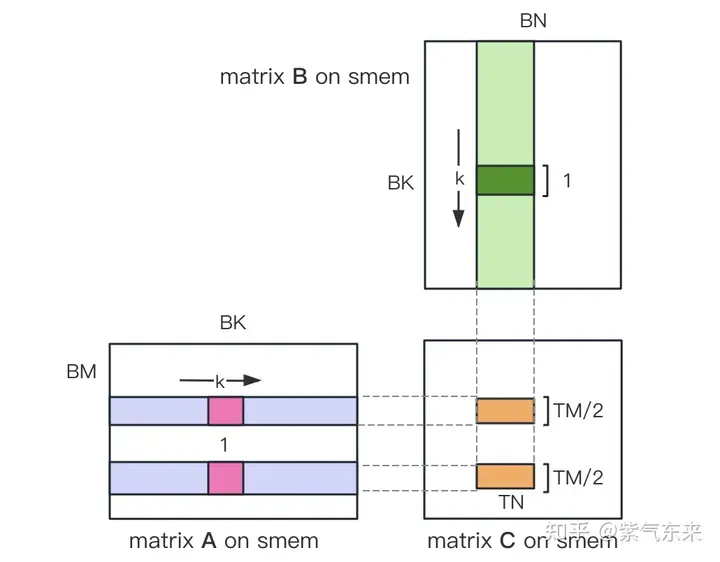
kernel 函数的核心部分实现如下，完整代码见 sgemm_v2.cu 。

__shared__ float s_a[BK][BM];__shared__ float s_b[BK][BN];float r_load_a[4];float r_load_b[4];float r_comp_a[TM];float r_comp_b[TN];float r_c[TM][TN] = {0.0};int load_a_smem_m = tid >> 1;int load_a_smem_k = (tid & 1) > 5;int load_b_smem_n = (tid & 31) 

结果如下，相对未解决 Bank Conflict 版(V1) 性能提高了 14.4%，达到了理论峰值的74.3%。

M N K =128128 1024, Time = 0.00029699 0.00029918 0.00030989 s, AVG Performance = 104.4530 GflopsM N K =192192 1024, Time = 0.00029776 0.00029828 0.00029882 s, AVG Performance = 235.7252 GflopsM N K =256256 1024, Time = 0.00029485 0.00029530 0.00029619 s, AVG Performance = 423.2949 GflopsM N K =384384 1024, Time = 0.00029734 0.00029848 0.00030090 s, AVG Performance = 942.2843 GflopsM N K =512512 1024, Time = 0.00029853 0.00029945 0.00030070 s, AVG Performance =1669.7479 GflopsM N K =768768 1024, Time = 0.00030458 0.00032467 0.00032790 s, AVG Performance =3465.1038 GflopsM N K = 1024 1024 1024, Time = 0.00032406 0.00032494 0.00032621 s, AVG Performance =6155.0281 GflopsM N K = 1536 1536 1024, Time = 0.00047990 0.00048224 0.00048461 s, AVG Performance =9331.3912 GflopsM N K = 2048 2048 1024, Time = 0.00094426 0.00094636 0.00094992 s, AVG Performance =8453.4569 GflopsM N K = 3072 3072 1024, Time = 0.00187866 0.00188096 0.00188538 s, AVG Performance =9569.5816 GflopsM N K = 4096 4096 1024, Time = 0.00312589 0.00319050 0.00328147 s, AVG Performance = 10029.7885 GflopsM N K = 6144 6144 1024, Time = 0.00641280 0.00658940 0.00703498 s, AVG Performance = 10926.6372 GflopsM N K = 8192 8192 1024, Time = 0.01101130 0.01116194 0.01122950 s, AVG Performance = 11467.5446 GflopsM N K =1228812288 1024, Time = 0.02464854 0.02466705 0.02469344 s, AVG Performance = 11675.4946 GflopsM N K =1638416384 1024, Time = 0.04385955 0.04387468 0.04388355 s, AVG Performance = 11669.5995 Gflops

分析一下 profiling 可以看到 Static Shared Memory 仍然是使用了8192 Bytes，奇怪的的是，Shared Memory executed 却翻倍变成了 16384 Bytes（知友如果知道原因可以告诉我一下）。

2.3 流水并行化：Double Buffering

Double Buffering，即双缓冲，即通过增加buffer的方式，使得 访存-计算 的串行模式流水线化，以减少等待时间，提高计算效率，其原理如下图所示:

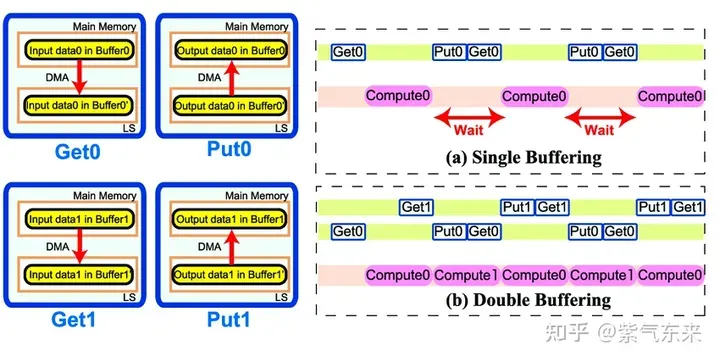
Single Buffering VS Double Buffering

具体到 GEMM 任务中来，就是需要两倍的Shared Memory，之前只需要BK * (BM + BN) * 4 Bytes的Shared Memory，采用Double Buffering之后需要2BK * (BM + BN) * 4 Bytes的Shared Memory，然后使其 pipeline 流动起来。

代码核心部分如下所示，完整代码参见 sgemm_v3.cu 。有以下几点需要注意：

1）主循环从bk = 1 开始，第一次数据加载在主循环之前，最后一次计算在主循环之后，这是pipeline 的特点决定的；

2）由于计算和下一次访存使用的Shared Memory不同，因此主循环中每次循环只需要一次__syncthreads()即可

3）由于GPU不能向CPU那样支持乱序执行，主循环中需要先将下一次循环计算需要的Gloabal Memory中的数据load 到寄存器，然后进行本次计算，之后再将load到寄存器中的数据写到Shared Memory，这样在LDG指令向Global Memory做load时，不会影响后续FFMA及其它运算指令的 launch 执行，也就达到了Double Buffering的目的。

__shared__ float s_a[2][BK][BM];__shared__ float s_b[2][BK][BN];float r_load_a[4];float r_load_b[4];float r_comp_a[TM];float r_comp_b[TN];float r_c[TM][TN] = {0.0};int load_a_smem_m = tid >> 1;int load_a_smem_k = (tid & 1) > 5;int load_b_smem_n = (tid & 31) 

性能如下所示，达到了理论峰值的 80.6%。

M N K =128128 1024, Time = 0.00024000 0.00024240 0.00025792 s, AVG Performance = 128.9191 GflopsM N K =192192 1024, Time = 0.00024000 0.00024048 0.00024125 s, AVG Performance = 292.3840 GflopsM N K =256256 1024, Time = 0.00024029 0.00024114 0.00024272 s, AVG Performance = 518.3728 GflopsM N K =384384 1024, Time = 0.00024070 0.00024145 0.00024198 s, AVG Performance =1164.8394 GflopsM N K =512512 1024, Time = 0.00024173 0.00024237 0.00024477 s, AVG Performance =2062.9786 GflopsM N K =768768 1024, Time = 0.00024291 0.00024540 0.00026010 s, AVG Performance =4584.3820 GflopsM N K = 1024 1024 1024, Time = 0.00024534 0.00024631 0.00024941 s, AVG Performance =8119.7302 GflopsM N K = 1536 1536 1024, Time = 0.00045712 0.00045780 0.00045872 s, AVG Performance =9829.5167 GflopsM N K = 2048 2048 1024, Time = 0.00089632 0.00089970 0.00090656 s, AVG Performance =8891.8924 GflopsM N K = 3072 3072 1024, Time = 0.00177891 0.00178289 0.00178592 s, AVG Performance = 10095.9883 GflopsM N K = 4096 4096 1024, Time = 0.00309763 0.00310057 0.00310451 s, AVG Performance = 10320.6843 GflopsM N K = 6144 6144 1024, Time = 0.00604826 0.00619887 0.00663078 s, AVG Performance = 11615.0253 GflopsM N K = 8192 8192 1024, Time = 0.01031738 0.01045051 0.01048861 s, AVG Performance = 12248.2036 GflopsM N K =1228812288 1024, Time = 0.02283978 0.02285837 0.02298272 s, AVG Performance = 12599.3212 GflopsM N K =1638416384 1024, Time = 0.04043287 0.04044823 0.04046151 s, AVG Performance = 12658.1556 Gflops

从 profiling 可以看到双倍的 Shared Memory 的占用

三、cuBLAS 实现方式探究

本节我们将认识CUDA的标准库——cuBLAS， 即NVIDIA版本的基本线性代数子程序 (Basic Linear Algebra Subprograms, BLAS) 规范实现代码。它支持 Level 1 (向量与向量运算) ，Level 2 (向量与矩阵运算) ，Level 3 (矩阵与矩阵运算) 级别的标准矩阵运算。

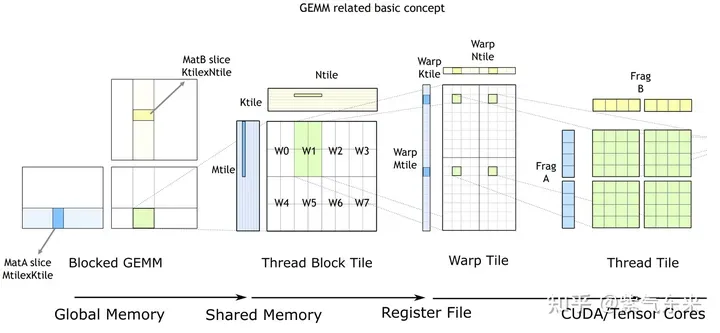
cuBLAS/CUTLASS GEMM的基本过程

如上图所示，计算过程分解成线程块片（thread block tile）、线程束片（warp tile）和线程片（thread tile）的层次结构并将AMP的策略应用于此层次结构来高效率的完成基于GPU的拆分成tile的GEMM。这个层次结构紧密地反映了NVIDIA CUDA编程模型。可以看到从global memory到shared memory的数据移动（矩阵到thread block tile）；从shared memory到寄存器的数据移动（thread block tile到warp tile）；从寄存器到CUDA core的计算（warp tile到thread tile）。

cuBLAS 实现了单精度矩阵乘的函数cublasSgemm，其主要参数如下：

cublasStatus_t cublasSgemm( cublasHandle_t handle, // 调用 cuBLAS 库时的句柄 cublasOperation_t transa, // A 矩阵是否需要转置 cublasOperation_t transb, // B 矩阵是否需要转置 int m, // A 的行数 int n, // B 的列数 int k, // A 的列数 const float *alpha, // 系数 α, host or device pointer const float *A, // 矩阵 A 的指针，device pointer int lda, // 矩阵 A 的主维，if A 转置， lda = max(1, k), else max(1, m) const float *B, // 矩阵 B 的指针, device pointer int ldb, // 矩阵 B 的主维，if B 转置， ldb = max(1, n), else max(1, k) const float *beta, // 系数 β, host or device pointer float *C, // 矩阵 C 的指针，device pointer int ldc // 矩阵 C 的主维，ldc >= max(1, m) );

调用方式如下：

cublasHandle_t cublas_handle;cublasCreate(&cublas_handle);float cublas_alpha = 1.0;float cublas_beta = 0;cublasSgemm(cublas_handle, CUBLAS_OP_N, CUBLAS_OP_N, N, M, K, &cublas_alpha, d_b, N, d_a, K, &cublas_beta, d_c, N);

性能如下所示，达到了理论峰值的 82.4%。

M N K =128128 1024, Time = 0.00002704 0.00003634 0.00010822 s, AVG Performance = 860.0286 GflopsM N K =192192 1024, Time = 0.00003155 0.00003773 0.00007267 s, AVG Performance =1863.6689 GflopsM N K =256256 1024, Time = 0.00003917 0.00004524 0.00007747 s, AVG Performance =2762.9438 GflopsM N K =384384 1024, Time = 0.00005318 0.00005978 0.00009120 s, AVG Performance =4705.0655 GflopsM N K =512512 1024, Time = 0.00008326 0.00010280 0.00013840 s, AVG Performance =4863.9646 GflopsM N K =768768 1024, Time = 0.00014278 0.00014867 0.00018816 s, AVG Performance =7567.1560 GflopsM N K = 1024 1024 1024, Time = 0.00023485 0.00024460 0.00028150 s, AVG Performance =8176.5614 GflopsM N K = 1536 1536 1024, Time = 0.00046474 0.00047607 0.00051181 s, AVG Performance =9452.3201 GflopsM N K = 2048 2048 1024, Time = 0.00077930 0.00087862 0.00092307 s, AVG Performance =9105.2126 GflopsM N K = 3072 3072 1024, Time = 0.00167904 0.00168434 0.00171114 s, AVG Performance = 10686.6837 GflopsM N K = 4096 4096 1024, Time = 0.00289619 0.00291068 0.00295904 s, AVG Performance = 10994.0128 GflopsM N K = 6144 6144 1024, Time = 0.00591766 0.00594586 0.00596915 s, AVG Performance = 12109.2611 GflopsM N K = 8192 8192 1024, Time = 0.01002384 0.01017465 0.01028435 s, AVG Performance = 12580.2896 GflopsM N K =1228812288 1024, Time = 0.02231159 0.02233805 0.02245619 s, AVG Performance = 12892.7969 GflopsM N K =1638416384 1024, Time = 0.03954650 0.03959291 0.03967242 s, AVG Performance = 12931.6086 Gflops

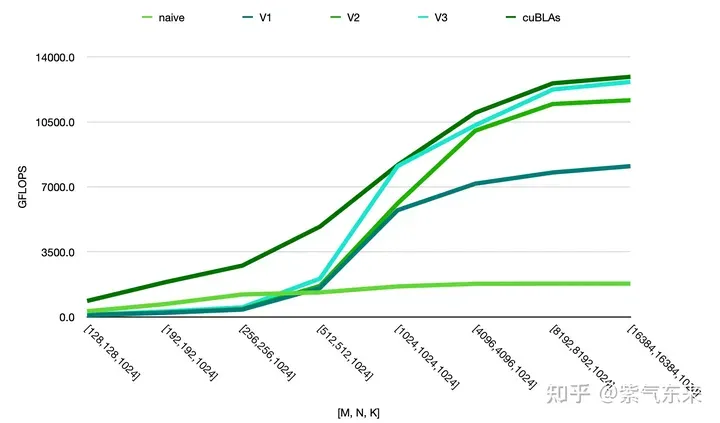
由此可以对比以上各种方法的性能情况，可见手动实现的性能已接近于官方的性能，如下：

以上是CUDA之通用矩阵乘法：从入门到熟练！的详细内容。更多信息请关注PHP中文网其他相关文章！