例如已知:梯形ABCD中,AD∥BC,AB=AD BC,E是CD的中点。求证:AE、BE分别平分∠BAD、∠ABC。
我们可以从已知条件出发,按照以下操作步骤,在几何画板中绘制出符合题意的图形。
打开几何画板,使用【点工具】在画板空白处任意画两点A、B,选择【射线工具】分别过点A、B画水平射线,选中点A、B执行构造线段。
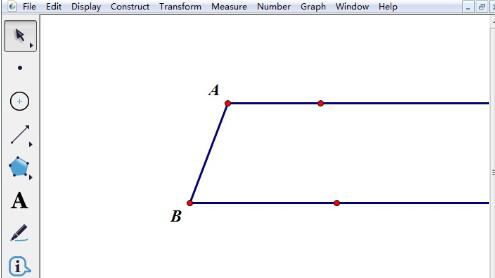
使用【点工具】在线段AB上任取一点F,分别以点A、B为圆心,以AF、BF长为半径作圆,与两底所在的射线交于点D、C,显然,AD BC=AB。
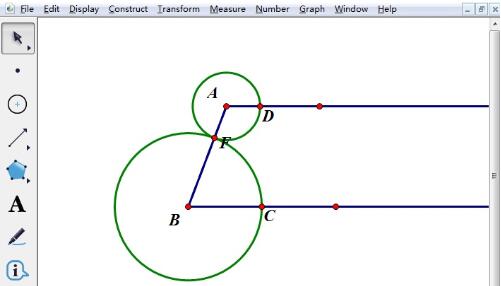
取线段CD的中点E,连结AE、BE。选中点C、D,执行【构造】——【中点】命令,画出中点E,依次选中点A、E,B、E,执行【构造】——【线段】命令,得到线段AE、BE。
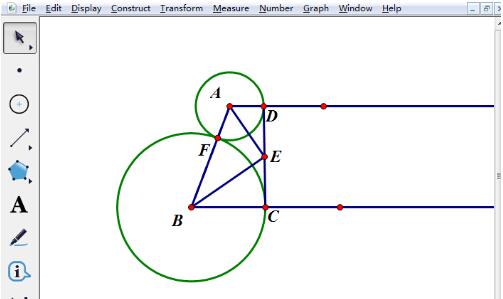
将作图过程中的辅助图形隐藏,即可得到符合题目要求的图形。选中不需要的射线、圆,按快捷键【Ctrl H】,就可以将不需要的对象隐藏,得到如图所示复合题意的图形。
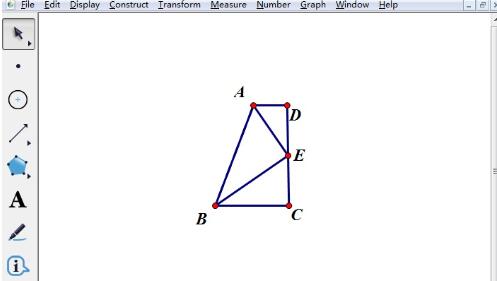
以上是几何画板中按已知条件绘制几何图形的操作方法的详细内容。更多信息请关注PHP中文网其他相关文章!




