无向图最小割问题取得新突破，谷歌研究获SODA 2024最佳论文奖

谷歌博客放出新研究，求解无向图的最小割问题。

1996 年， 美国计算机科学家 David R Karger 连同其他研究者在论文《 A new approach to the minimum cut problem》中提出了一个令人惊讶的随机算法 Karger 算法，其在理论计算机科学中非常重要，尤其适用于大规模图的近似最小割问题。

Karger 算法可以在时间为 O (m log^3n) 的图中找到一个最小割点，他们将这个时间称之为近线性时间，意思是线性乘以一个多对数因子。

在谷歌刚刚更新的一篇博客中，他们介绍了之前发布的一篇论文《 Deterministic Near-Linear Time Minimum Cut in Weighted Graphs 》，研究获得了 ACM-SIAM SODA24 最佳论文奖。文章详细阐述了一个几乎是线性时间内（而不是近线性时间）运行的新算法，这个算法是确定性的，能够可靠地找到正确的最小割，改进了之前可能无法保证结果正确或只适用于简单图的算法。可以说这是自 Karger 著名的随机化算法以来的重大发现。

• 论文地址：https://arxiv.org/pdf/2401.05627.pdf
• 论文标题：Deterministic Near-Linear Time Minimum Cut in Weighted Graphs

注：最小割问题（通常称为最小割）是关于图连通性的基本结构问题，它一般关注的是断开网络最简单的方法是什么？在图论中，去掉其中所有边能使一张网络流图不再连通（即分成两个子图）的边集称为图的割，一张图上最小的割称为最小割。

                               ^{一张图及其两个割：红色点线标出了一个包含三条边的割，绿色划线则表示了这张图的一个最小割（包含两条边）。}

方法介绍

关于最小割问题，Karger 在 1996 年开创性的给出了一个近乎线性的时间随机算法，该算法能够以较高的概率找到最小割，并且该工作还给出了一个关键见解，即存在一个更小的图，它在很大程度上保留了所有割的大小。

这个发现是很有用的，因为可以使用较小的图作为输入来运行较慢的算法，并且较慢的运行时间（就较小的图的大小而言）仍然可以与原始（较大）图的大小接近线性。

事实上，关于最小割问题的许多结构发现都是沿着这个方向进行的。

谷歌是这样做的，从具有 n 个节点的图 G 开始，然后依据论文《 Randomized Approximation Schemes for Cuts and Flows in Capacitated Graphs 》（作者为 Benzur、Karger）提出的割保留稀疏化方法，证明了可以构造一个边数更少的稀疏加权图 G'，且在这个图上，几乎所有割的大小与原图 G 中相应割的大小大致相同。

这个概念可以通过以下例子来说明：原始图由两个通过单一边连接的完全图组成，而稀疏化后的图边数更少，但边的权重更大，同时所有割的大小大致得以保留。

为了构建这种较稀疏的图，Benzur 和 Karger 采用了独立采样边的方法。在这种方法中，图 G 中的每条边都有一定概率被包含在图 G' 中，并且其在 G' 中的权重会根据采样概率的倒数进行放大（例如，如果一条原权重为 1 的边以 10% 的概率被包含，则其权重调整为 10）。结果表明，这种非常简单（几乎是线性时间）的方法具有很高的成功概率，可以构建出保持割的图稀疏化。

然而，Karger 算法是一种蒙特卡洛算法，即输出可能小概率不正确，并且除了与实际已知的最小割进行比较之外，没有已知的方法可以判断输出是否正确。

因此，研究人员一直在努力探索解决近线性时间确定性算法开放问题的方法。由于 cut-preserving 图稀疏化的构造是 Karger 算法中唯一随机的组成部分，因此一种方法是在近线性时间内找到稀疏化的确定性构造（也称为去随机化）。

2015 年，Kawarabayashi 和 Thorup 实现了一个重要的里程碑 —— 找到针对简单图（即每对节点之间至多有一条边且所有边权重等于 1 的图）的确定性近线性时间算法。

该研究得出一个关键思路，即最小割和另一个重要的图结构（称为「low-conductance cut」）之间存在一些联系。这种联系对于后来在一般边权重图上去随机化 Karger 算法至关重要，并帮助谷歌得出了新算法。

最小割和 low-conductance cut 的对齐

图割 S 的 conductance 定义为 S 的 cut 大小与 S 的 volume 之比（假设 S 是切口的较小体积侧且非空），其中 S 的 volume 是 S 中节点的度数。

low-conductance 的 cut S 直观地捕获了网络中的瓶颈，因为只有少量边（相对于其 volume）将 S 连接到图的其余部分。图的 conductance 被定义为图中任何 cut 的最小 conductance，并且大 conductance 的图（也称为扩展图）被认为是良好连接的，因为内部没有瓶颈。

                              ^{红色虚线表示 cut 大小为 2，较小的一侧（底部）volume 为 24，因此其 conductance 为 1/12，这也是图的 conductance。}

Kawayabarashi 和 Thorup 观察到，在最小节点度数较大的简单图中，任何非平凡（即两侧至少有两个节点）最小割都必须具有 low conductance。根据这一观察，如果可以将图划分为连接良好的簇（cluster），则划分必须与每个非平凡最小割一致，因为每个簇必须完全位于每个 cut 的一侧。然后，将每个簇收缩为一个节点，并处理较小的图，其中原始图的所有非平凡最小割都完好无损。

然而，对于加权图，上述观察不再成立，并且简单图情况中使用的相同划分可能与非平凡最小割不完全一致。

如下图所示，Jason Li 2021 年观察到，这种划分仍然与非平凡最小割大致一致。特别地，对于非平凡最小割 S，存在与 S 相差不大的 cut S'，使得 S' 与簇一致。Jason Li 进一步观察到，可以利用划分的这种特性来有效地去随机化 cut-preserving 图稀疏化的构造。

谷歌设计的新算法旨在构建一种划分，来制定最小割的用例。与 Jason Li 在之前的工作中使用的更通用的现成方法相比，谷歌的这项研究更加精确、更加快捷。新研究在保证精度的同时在运行时间上也进行了优化，最终实现了针对最小割问题的近线性时间确定性算法。

^{参考链接：https://research.google/blog/solving-the-minimum-cut-problem-for-undirected-graphs/}

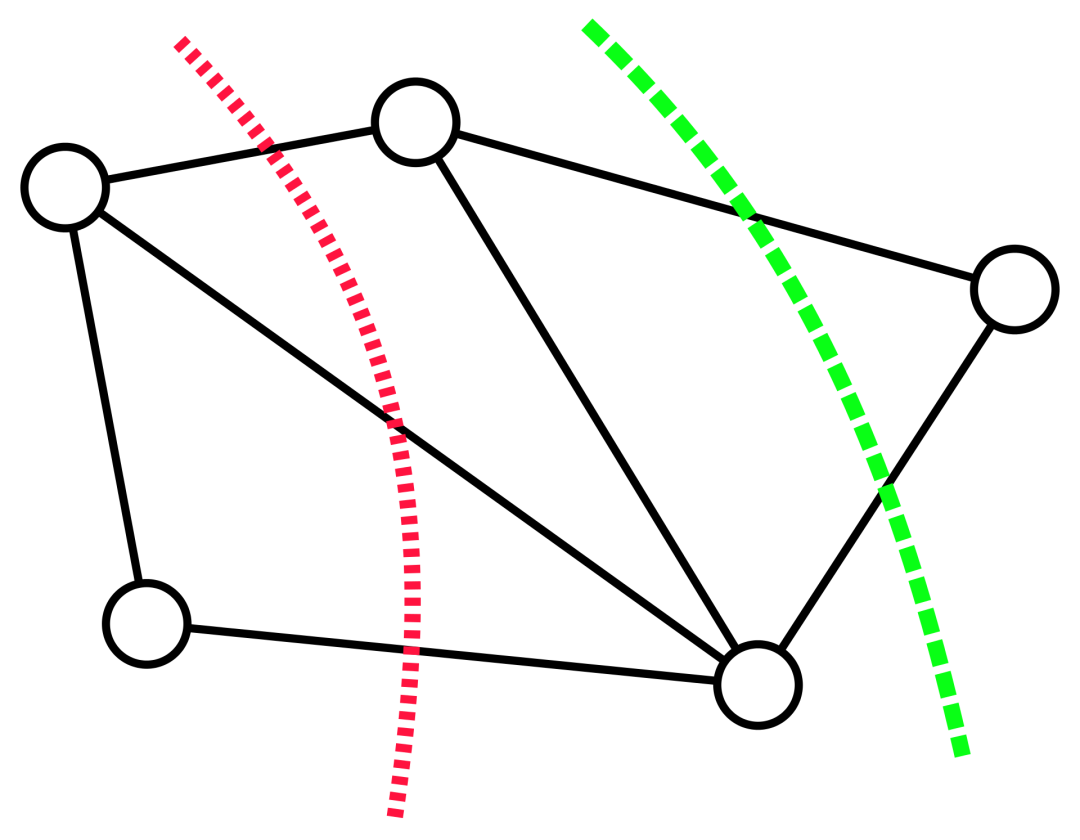
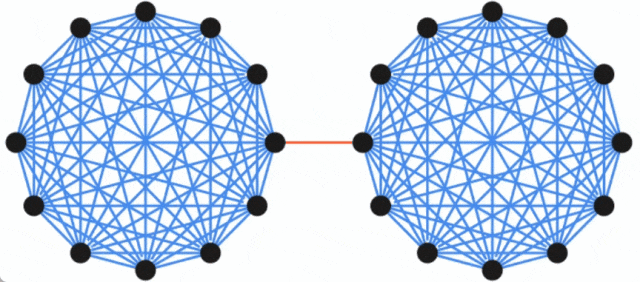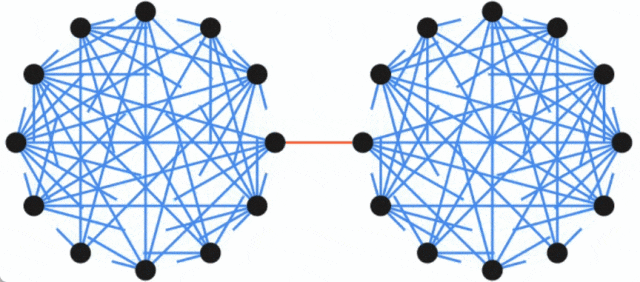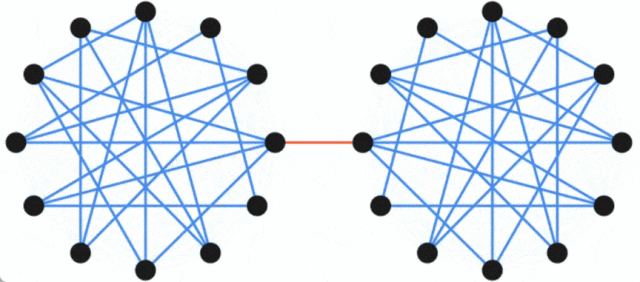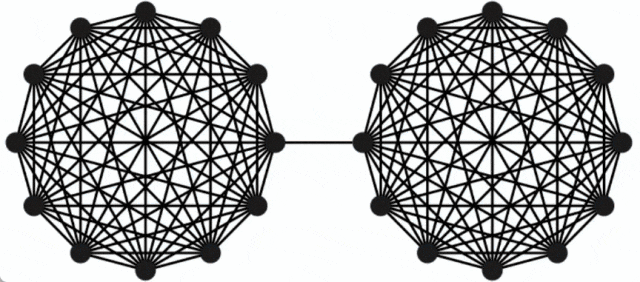
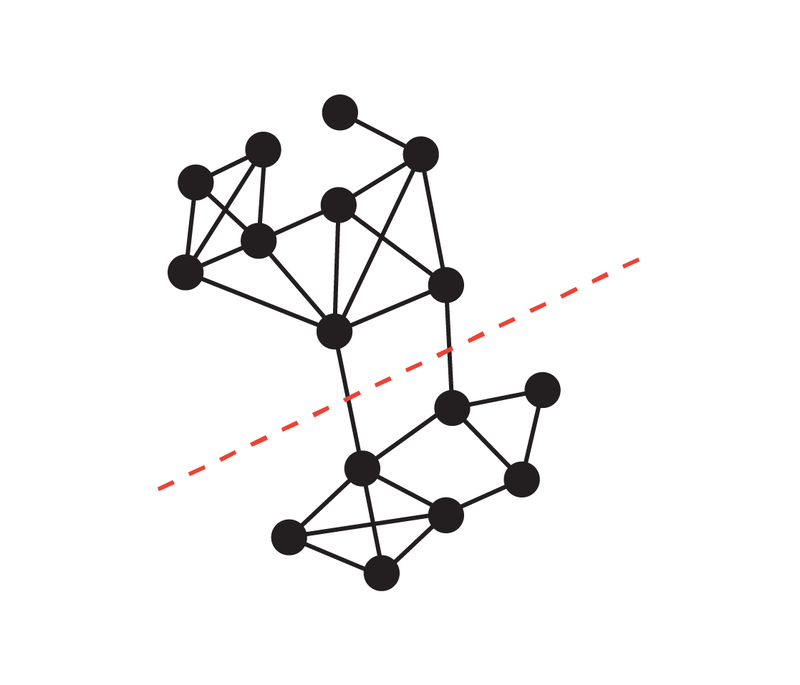
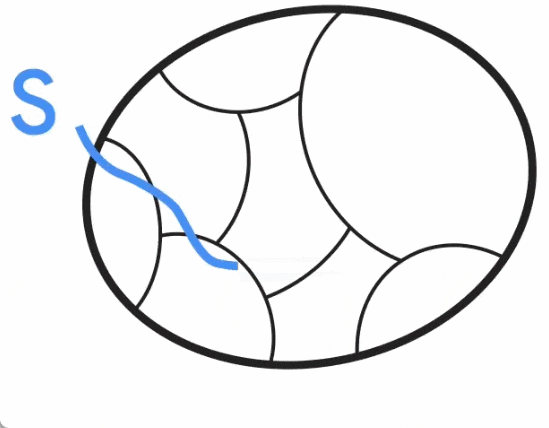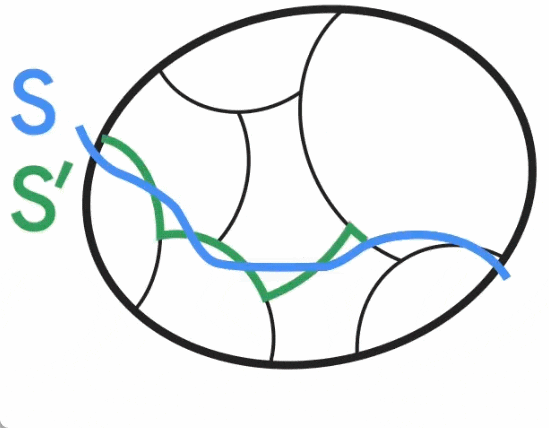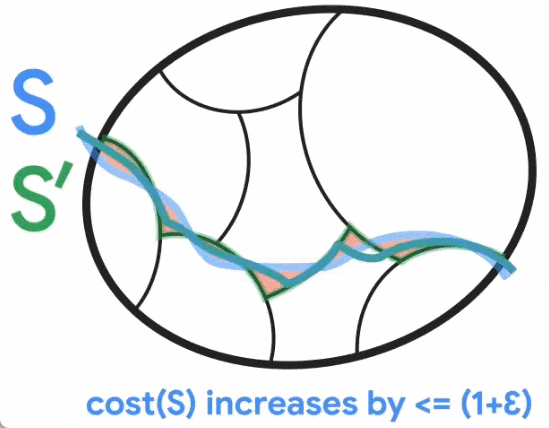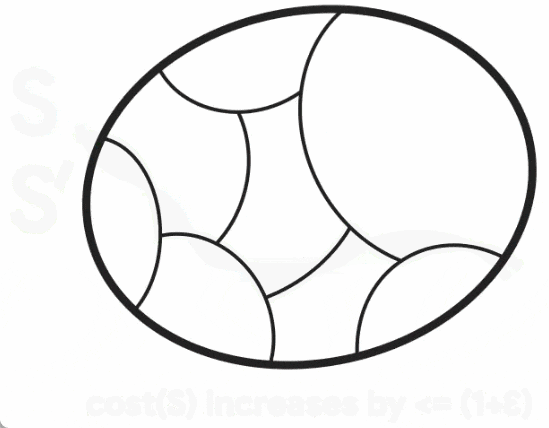
以上是无向图最小割问题取得新突破，谷歌研究获SODA 2024最佳论文奖的详细内容。更多信息请关注PHP中文网其他相关文章！