跨越300多年的接力：受陶哲轩启发，数学家决定用AI形式化费马大定理的证明

在陶哲轩的启发下，越来越多的数学家开始尝试利用人工智能进行数学探索。这次，他们瞄准的目标是世界十大最顶尖数学难题之一的费马大定理。费马大定理是一个非常复杂的数学难题，迄今为止尚未找到可行的解法。数学家们希望借助人工智能的强大计算能力和智能算法，能够在数学探索

费马大定理又被称为“费马最后的定理（Fermat's Last Theorem，FLT）”，由17世纪法国数学家皮耶・德・费马提出。它背后有一个传奇的故事。据称，大约在1637年左右，费马在阅读丢番图《算术》拉丁文译本时，曾在第11卷第8命题旁写道：“将一个立方数分成两个立方数之和，或一个四次幂分成两个四次幂之和，或者一般地将一个高于二次幂的幂分成两个同次幂之和，这是不可能的。”关于此，我确信已经发现了一种美妙的证法 ，可惜这里空白的地方太小，写不下了。”

这段话前面所表述的就是费马大定理的内容：当整数 n>2 时，关于 x^n y^n=z^n 的方程没有正整数解。

费马表示，自己知道怎么证明，但因为书的空白部分太小，就没写。对于该故事的真实性以及费马是否真的想出了证明方法，后世是存有争议的。

在之后的300多年里，数学家们一直在努力，接力证明费马大定理。直到1995年，美国普林斯顿大学的Andrew Wiles教授经过8年的孤军奋战，终于用130页长的篇幅完成了证明。Wiles也成为整个数学界的英雄。

既然费马大定理已经被证明了，数学家还能用 AI 做什么呢？答案是：形式化它的证明。

数学的形式化通常指的是使用严格的形式语言（如逻辑和集合论）来表述数学对象、结构、定理和证明，使其能够在计算机上进行表示、验证和操作，从而保证数学内容的准确性和一致性。形式化数学的发展可以追溯到19世纪末和20世纪初，而现代的形式化数学则始于20世纪的数理逻辑和计算机科学的发展。 形式化数学的主要目标是建立一套形式系统，其中包括一组符号、一组基本公理和一组推理规则，通过这些规则和公理的运用，可以进行

去年年底，陶哲轩等人曾用 Lean（一款交互式定理证明器，也是一门编程语言）形式化了他们的一篇论文。这篇论文是对多项式 Freiman-Ruzsa 猜想的一个版本的证明，于去年 11 月发布在 arXiv 上。在编写 Lean 语言代码的时候，陶哲轩还借助了 AI 编程助手 Copilot。该事件引起数学界和人工智能界的广泛关注。

当时，Lean 技术开源社区最重要的推广者、伦敦帝国理工学院的 Kevin Buzzard 表示：「从根本上来说，显而易见的是，当你将某些东西数字化时，你就可以以新的方式使用它。我们将把数学数字化，这会让数学变得更好。」

这位 Buzzard 教授，就是最近宣称要形式化费马大定理证明的数学家，他所用的工具也是 Lean。

在一篇博客中，他介绍了自己做这件事情的背景、动机以及具体的做法。

为什么要形式化费马大定理的证明？

费马大定理的形式非常简洁、直观，然而证明它却异常艰难。这无疑是对数学深邃之美的一次绝佳展示。在过去的几个世纪中，为了解决这个问题，数学家们发展和创新了大量数学理论，这些理论在密码学到物理学等多个领域都有所应用。

Andrew Wiles 可能因 FLT 而受到启发，但他的工作实际上为朗兰兹计划带来了突破，该计划是数学中一系列影响深远的构想，联系数论、代数几何与约化群表示理论，且在 2024 年依然备受关注。

历史上，代数数论的其他几个重大突破（例如数域中的因式分解理论和循环域的算术）至少部分是出于对 FLT 更深层次理解的渴望。

Wiles 的工作，由他的学生 Richard Taylor 一起补充完整，建立在 20 世纪数学的庞大基础之上。Wiles 引入的基本技术 ——「模性提升定理（modularity lifting theorem）」—— 在原始论文发表后的 30 年间，在概念上被极大简化和广泛推广。这一领域至今仍然非常活跃。Frank Calegari 在 2022 年国际数学家大会上的论文，概述了自 Wiles 突破以来的进展（参见：https://arxiv.org/abs/2109.14145）。Kevin Buzzard 表示，这一领域的持续活跃，是他将 FLT 证明形式化的动机之一。

数学的形式化，即将纸上的数学转换为能够理解定理和证明概念的计算机编程语言的艺术。这些编程语言，也称为交互式定理证明器（ITP），已经存在了数十年。然而，近年来，这一领域似乎吸引了数学界的一部分关注。我们已经见证了多个研究数学形式化的例子，其中最新的是陶哲轩等人对多项式 Freiman—Ruzsa 猜想证明的形式化。这篇 2023 年的突破性论文在短短三周内就在 Lean 中完成了形式化。这样的成功案例可能会让旁观者认为，像 Lean 这样的 ITP 现在已经准备好形式化所有现代数学了。

然而，真相远非如此简单。在数学的某些领域，例如组合学，我们可以看到一些现代突破可以实时形式化。然而，Buzzard 表示，他定期参加伦敦数论研讨会，经常注意到 Lean 对现代数学定义的了解还不足以表述研讨会上宣布的结果，更不用说验证它们的证明了。

事实上，数论在这一方面的「滞后」是 Buzzard 启动 FLT 当代证明形式化的主要动机之一。在项目完成之前，Lean 将能够理解自守形式（一类特别的复变量函数）和表示、伽罗瓦表示、潜在自守性、模性提升定理、代数簇的算术、类域论、算术对偶定理、志村簇等现代代数数论中使用的概念。在 Buzzard 看来，有了这些做基础，将他自己专业领域正在发生的事情形式化将不再是科幻小说。

那么，为什么要这么做呢？Buzzard 解释说，「如果我们相信一些计算机科学家的话，人工智能的指数级增长终将使计算机能够帮助数学家进行研究。这样的工作可以帮助计算机理解我们在现代数学研究中正在做的事情。」

项目如何开展？  

费马大定理的形式化项目现已启动。Buzzard 在一幅图中展示了当前的进展。

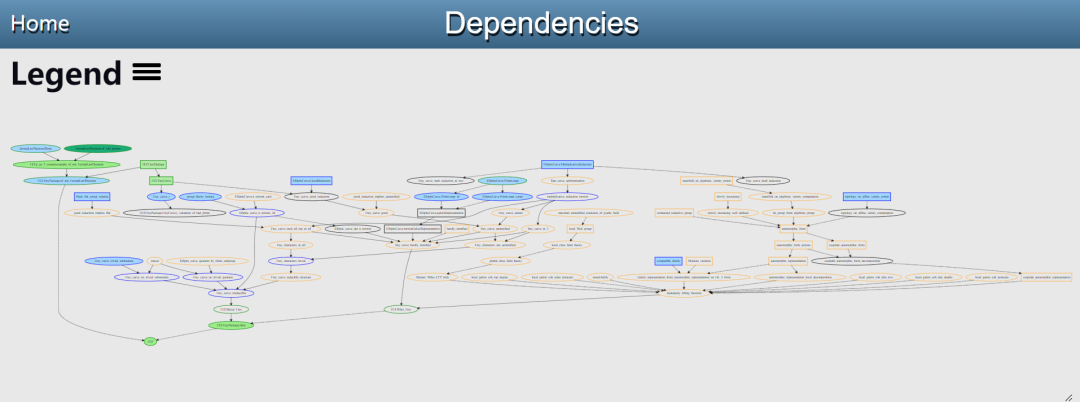
感兴趣的研究者可以阅读详情：https://imperialcollegelondon.github.io/FLT/blueprint/dep_graph_document.html

该项目由 EPSRC 资助，Buzzard 将获得前五年的资金支持。在此期间，他的第一个目标是将 FLT 简化为 1980 年代末数学家已知的声明。

当然，Buzzard 没有打算独自完成这件事情。他表示，对于有些论证的部分，他理解其基本原则，但从未仔细检查过细节。而且，朗兰兹计划还引入了一些重要的东西，包括 GL_2 的循环基变换以及 Jacquet-Langlands。对于这些深奥的东西，他的理解还不够深。

不过，这恰恰是形式化项目的优势所在。Buzzard 将能够在 Lean 中明确表述他需要的结果，并将它们传递给其他人。这个系统的美妙之处在于：你不必理解 FLT 的整个证明就能做出贡献。上面的图将证明分解为许多小引理，因此非常方便进行众包操作。如果你能形式化证明其中任何一个引理，那么 Buzzard 会热切期待你的拉取请求。

想要参与项目的人需要了解一些关于 Lean 的知识。对此，Buzzard 推荐了在线教科书 Mathematics in Lean。

教科书链接：https://leanprover-community.github.io/mathematics_in_lean/

该项目将在 Lean Zulip chat 的 FLT  stream 上进行，这是一个强大的研究论坛，数学家和计算机科学家可以实时协作，轻松地发布代码和数学，使用线程和 stream 系统，有效地支持多场独立对话同时进行。

Lean Zulip chat 链接：https://leanprover.zulipchat.com/

Buzzard 表示，他对这个项目将需要多长时间没有任何预感，但他绝对乐观。

与此同时，像 Lean 这类形式化证明工具也在不断迭代。相比初代 Lean，现在最新的 Lean 4 版本进行了多项优化，包括更快的编译器、改进的错误处理和更好的与外部工具集成的能力等。

去年年底，开放平台 LeanDojo 团队和加州理工学院的研究者还推出了 Lean Copilot，这是一款专为大型语言模型与人类交互而设计的协作工具，为数学研究注入了 AI 大模型的力量。

「我预计，如果使用得当，到 2026 年，AI 将成为数学研究和许多其他领域值得信赖的合著者。」陶哲轩在之前的一篇博客中说道。

希望陶哲轩的预言早日成真。

相关阅读：

• 《陶哲轩用 AI 形式化的证明究竟是什么？一文看懂 PFR 猜想的前世今生》

• 《陶哲轩青睐的证明助手Lean，用上了大模型》

• 《大模型帮陶哲轩解题、证明数学定理：数学真要成为首个借助AI实现突破的学科了？》

• 《陶哲轩上新项目：Lean中证明素数定理，研究蓝图都建好了》

^{参考链接：https://leanprover.zulipchat.com/#narrow/stream/416277-FLT}

^{https://mp.weixin.qq.com/s/d9RSkRhlKH5ZMek3yTqe4Q}

以上是跨越300多年的接力：受陶哲轩启发，数学家决定用AI形式化费马大定理的证明的详细内容。更多信息请关注PHP中文网其他相关文章！