浅谈javascript实现八大排序_javascript技巧

开学一个月，已经多次梦见笔试出现数据结构算法题，我对数据结构的恐惧已经多于任何“妖魔鬼怪”了。呵呵，看来真的很有必要复习一下常用的数据结构，免得“噩梦”成真。

数据机构等编程基础的重要性不用多说，直接进入正题。

排序算法，分为内部排序和外部排序。内部排序要使用内存，这里只探讨内部排序。

1，插入排序：直接插入排序和希尔排序

2，选择排序：简单选择排序和堆排序

3，交换排序：冒泡排序和快速排序

4，归并排序

5，基数排序

直接插入排序

基本思想：在要排序的一组数，假设前面（n-1）[n>=2]个数已经是排好顺序的，先要把第n个数插入到前面的有序数，使得这n个数也是排好顺序的。如此反复循环，知道全部排好顺序。

希尔排序

基本思想：算法先将要排序的一组数按某个增量d（n/2，n为要排序的个数）分成若干组，每组中记录的下标相差d。对每组中全部元素进行直接插入排序，然后再用一个较小的增量（d/2）对它进行分组，在每组中再进行直接插入排序。当增量减到1时，进行直接插入排序后，排序完成。

简单选择排序

基本思想：在要排序的一组数中，选出最小的一个数与第一个位置的数交换，然后剩下的数当中找出最小的与第二个位置的数交换，如此寻哈un到倒数第二个数和最后一个数为止。

堆排序

基本思想：堆排序是一种树形选择排序，是对直接选择排序的有效改进。

具有n个元素的序列（h1,h2,...,hn),当且仅当满足（hi>=h2i,hi>=2i+1）或（hi

冒泡排序

基本思想：在要排序的一组数中，对当前还未排好序的范围内的全部数，自上而下对相邻的两个数依次进行比较和调整，让较大的数往下沉，较小的往上冒。即：每当两相邻的数比较后发现它们的排序与排序要求相反时，就将它们互换。

快速排序

基本思想：选择一个基准元素,通常选择第一个元素或者最后一个元素,通过一趟扫描，将待排序列分成两部分,一部分比基准元素小,一部分大于等于基准元素,此时基准元素在其排好序后的正确位置,然后再用同样的方法递归地排序划分的两部分。

归并排序

基本排序：归并（Merge）排序法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

基数排序

基本思想：将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。

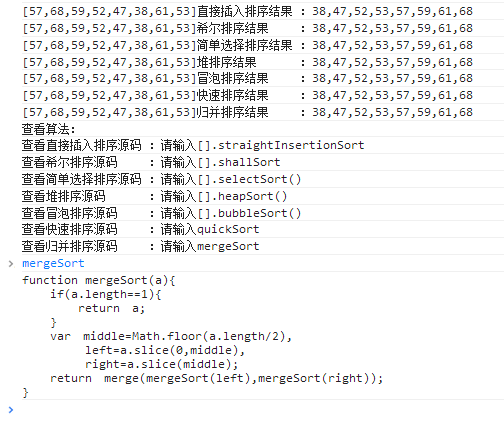
代码演示地址：http://lovermap.sinaapp.com/test/sort.html

现在我们分析一下8种排序算法的稳定性。

（请网友结合前面的排序基本思想来理解排序的稳定性（8种排序的基本思想已经在前面说过，这里不再赘述）不然可能有些模糊）

（1）直接插入排序：一般插入排序，比较是从有序序列的最后一个元素开始，如果比它大则直接插入在其后面，否则一直往前比。如果找到一个和插入元素相等的，那么就插入到这个相等元素的后面。插入排序是稳定的。

（2）希尔排序：希尔排序是按照不同步长对元素进行插入排序，一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，稳定性就会被破坏，所以希尔排序不稳定。

（3）简单选择排序：在一趟选择，如果当前元素比一个元素小，而该小的元素又出现在一个和当前元素相等的元素后面，那么交换后稳定性就被破坏了。光说可能有点模糊，来看个小实例：858410，第一遍扫描，第1个元素8会和4交换，那么原序列中2个8的相对前后顺序和原序列不一致了，所以选择排序不稳定。

（4）堆排序：堆排序的过程是从第n/2开始和其子节点共3个值选择最大(大顶堆)或者最小(小顶堆),这3个元素之间的选择当然不会破坏稳定性。但当为n/2-1, n/2-2, ...这些父节点选择元素时，有可能第n/2个父节点交换把后面一个元素交换过去了，而第n/2-1个父节点把后面一个相同的元素没有交换，所以堆排序并不稳定。

（5）冒泡排序：由前面的内容可知，冒泡排序是相邻的两个元素比较，交换也发生在这两个元素之间，如果两个元素相等，不用交换。所以冒泡排序稳定。

（6）快速排序：在中枢元素和序列中一个元素交换的时候，很有可能把前面的元素的稳定性打乱。还是看一个小实例：6 4 4 5 4 7 8 9，第一趟排序，中枢元素6和第三个4交换就会把元素4的原序列破坏，所以快速排序不稳定。

（7）归并排序：在分解的子列中，有1个或2个元素时，1个元素不会交换，2个元素如果大小相等也不会交换。在序列合并的过程中，如果两个当前元素相等时，我们把处在前面的序列的元素保存在结果序列的前面，所以，归并排序也是稳定的。

（8）基数排序：是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序，最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。基数排序基于分别排序，分别收集，所以是稳定的。

8种排序的分类，稳定性，时间复杂度和空间复杂度总结：

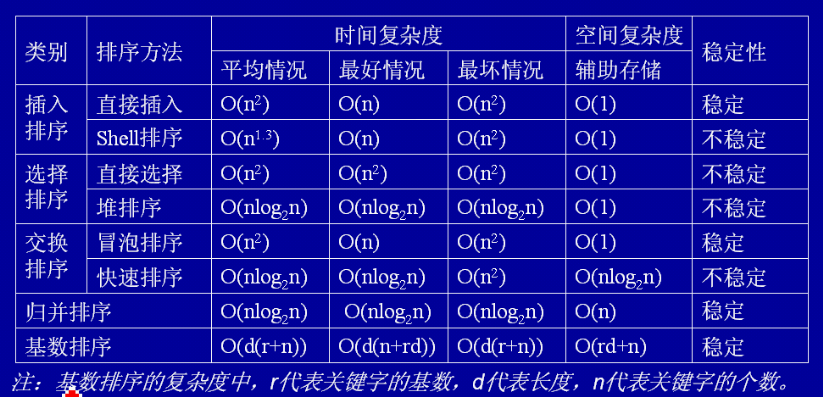
以上所述就是本文的全部内容了，希望大家能够喜欢。