多层感知器（MLP），也被称为全连接前馈神经网络，是如今深度学习模型的基础构建块。MLP 的重要性无论如何强调都不为过，因为它们是机器学习中用于逼近非线性函数的默认方法。
但是最近，来自 MIT 等机构的研究者提出了一种非常有潜力的替代方法 ——KAN。该方法在准确性和可解释性方面表现优于 MLP。而且，它能以非常少的参数量胜过以更大参数量运行的 MLP。比如，作者表示，他们用 KAN 重新发现了结理论中的数学规律，以更小的网络和更高的自动化程度重现了 DeepMind 的结果。具体来说，DeepMind 的 MLP 有大约 300000 个参数，而 KAN 只有大约 200 个参数。
微调内容如下：
这些惊人的研究成果让KAN迅速走红，吸引了很多人对其展开研究。很快，有人提出了一些质疑。其中，有一篇标题为“KAN is just MLP”的Colab文档成为了讨论的焦点。
KAN 只是一个普通的 MLP？
上述文档的作者表示，你可以把 KAN 写成一个 MLP，只要在 ReLU 之前加一些重复和移位。
在一个简短的示例中，作者展示了如何将KAN网络改写为具有相同数量参数的、具有轻微的非线性结构的普通MLP。
需要记住的是，KAN 在边上有激活函数。他们使用 B 样条。在展示的例子中，为了简单起见，作者将只使用 piece-wise 线性函数。这不会改变网络的建模能力。
下面是 piece-wise 线性函数的一个例子：
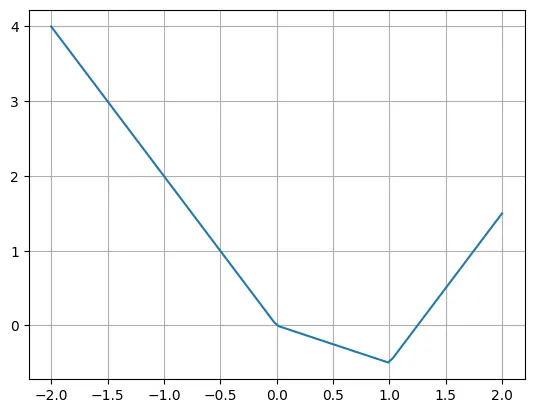
作者表示，我们可以使用多个 ReLU 和线性函数轻松重写这个函数。请注意，有时需要移动 ReLU 的输入。
plt.plot(X, -2*X + torch.relu(X)*1.5 + torch.relu(X-1)*2.5)plt.grid()
登录后复制
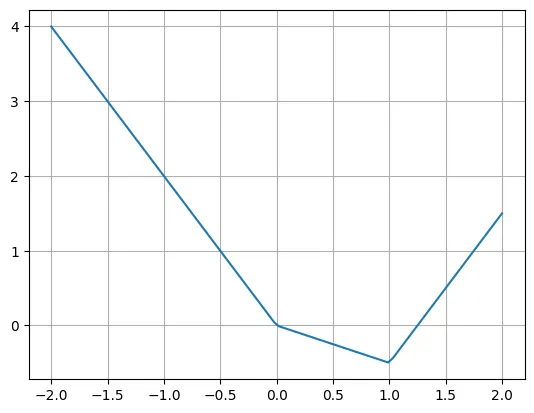
真正的问题是如何将 KAN 层改写成典型的 MLP 层。假设有 n 个输入神经元，m 个输出神经元，piece-wise 函数有 k 个 piece。这需要 n∗m∗k 个参数（每条边有 k 个参数，而你有 n∗m 条边）。
现在考虑一个 KAN 边。为此，需要将输入复制 k 次，每个副本移动一个常数，然后通过 ReLU 和线性层（第一层除外）运行。从图形上看是这样的（C 是常数，W 是权重）：
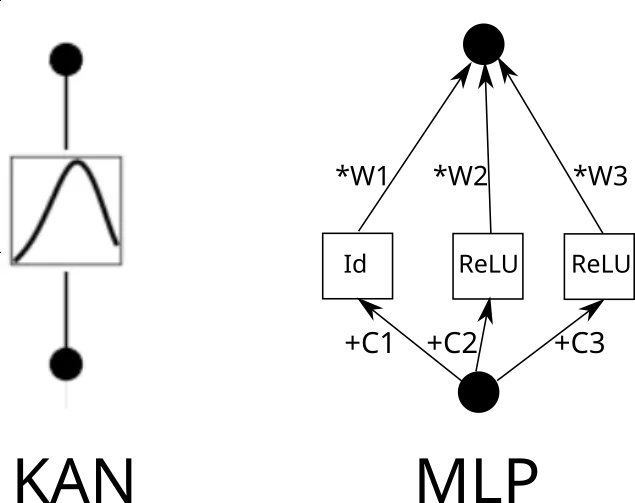
现在，可以对每一条边重复这一过程。但要注意一点，如果各处的 piece-wise 线性函数网格相同，我们就可以共享中间的 ReLU 输出，只需在其上混合权重即可。就像这样：
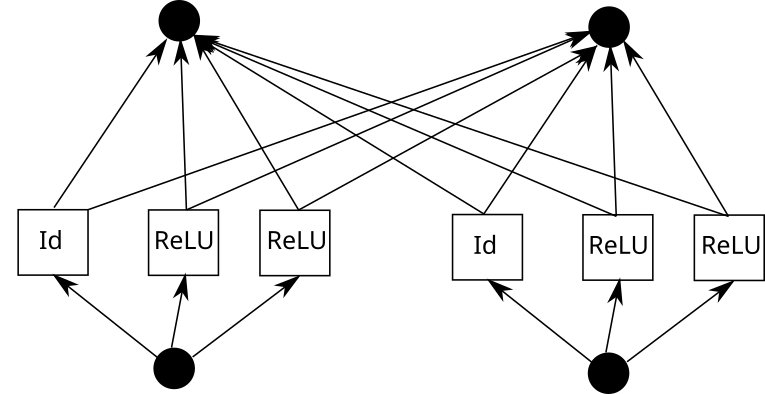
在 Pytorch 中，这可以翻译成以下内容：
k = 3 # Grid sizeinp_size = 5out_size = 7batch_size = 10X = torch.randn(batch_size, inp_size) # Our inputlinear = nn.Linear(inp_size*k, out_size)# Weightsrepeated = X.unsqueeze(1).repeat(1,k,1)shifts = torch.linspace(-1, 1, k).reshape(1,k,1)shifted = repeated + shiftsintermediate = torch.cat([shifted[:,:1,:], torch.relu(shifted[:,1:,:])], dim=1).flatten(1)outputs = linear(intermediate)
登录后复制
现在我们的层看起来是这样的：
一个接一个地考虑三个层：
- Expand shift ReLU (第 1 层从这里开始)
- Linear
- Expand shift ReLU (第 2 层从这里开始)
- Linear
- Expand shift ReLU (第 3 层从这里开始)
- Linear
忽略输入 expansion，我们可以重新排列：
- Linear (第 1 层从这里开始)
- Expand shift ReLU
- Linear (第 2 层从这里开始)
- Expand shift ReLU
如下的层基本上可以称为 MLP。你也可以把线性层做大，去掉 expand 和 shift，获得更好的建模能力（尽管需要付出更高的参数代价）。
- Linear (第 2 层从这里开始)
- Expand shift ReLU
通过这个例子，作者表明，KAN 就是一种 MLP。这一说法引发了大家对两类方法的重新思考。
对 KAN 思路、方法、结果的重新审视
其实，除了与 MLP 理不清的关系，KAN 还受到了其他许多方面的质疑。
总结下来，研究者们的讨论主要集中在如下几点。
第一，KAN 的主要贡献在于可解释性，而不在于扩展速度、准确性等部分。
论文作者曾经表示：
- KAN 的扩展速度比 MLP 更快。KAN 比参数较少的 MLP 具有更好的准确性。
- KAN 可以直观地可视化。KAN 提供了 MLP 无法提供的可解释性和交互性。我们可以使用 KAN 潜在地发现新的科学定律。
其中，网络的可解释性对于模型解决现实问题的重要性不言而喻：
但问题在于：「我认为他们的主张只是它学得更快并且具有可解释性，而不是其他东西。如果 KAN 的参数比等效的 NN 少得多，则前者是有意义的。我仍然感觉训练 KAN 非常不稳定。」
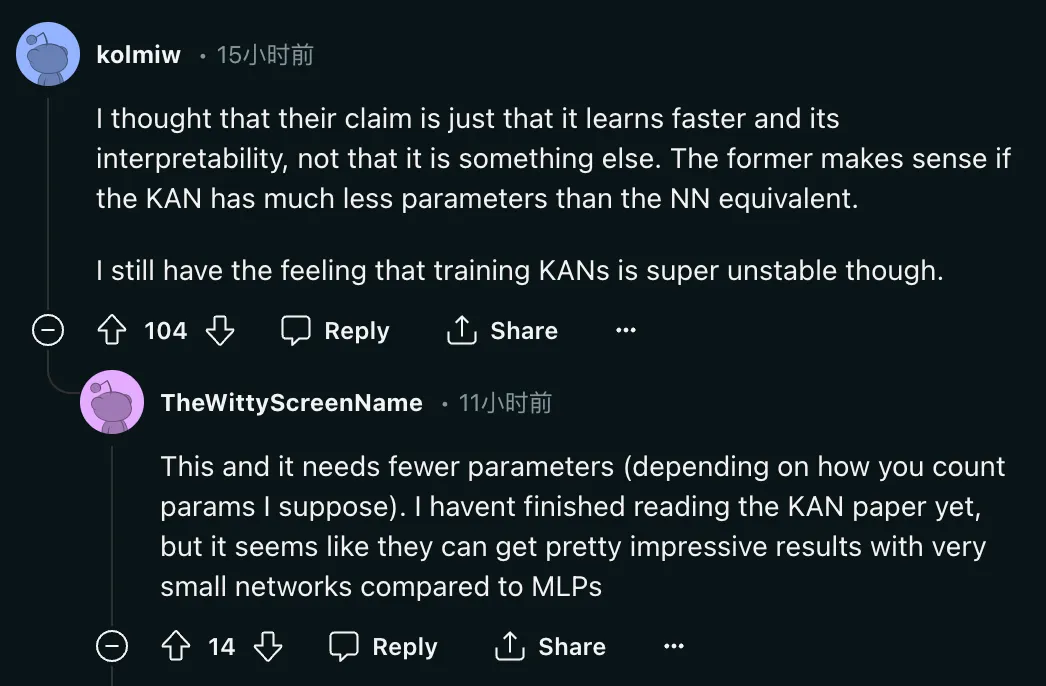
那么 KAN 究竟能不能做到参数比等效的 NN 少很多呢？
这种说法目前还存在疑问。在论文中，KAN 的作者表示，他们仅用 200 个参数的 KAN，就能复现 DeepMind 用 30 万参数的 MLP 发现数学定理研究。在看到该结果后，佐治亚理工副教授 Humphrey Shi 的两位学生重新审视了 DeepMind 的实验，发现只需 122 个参数，DeepMind 的 MLP 就能媲美 KAN 81.6% 的准确率。而且，他们没有对 DeepMind 代码进行任何重大修改。为了实现这个结果，他们只减小了网络大小，使用随机种子，并增加了训练时间。
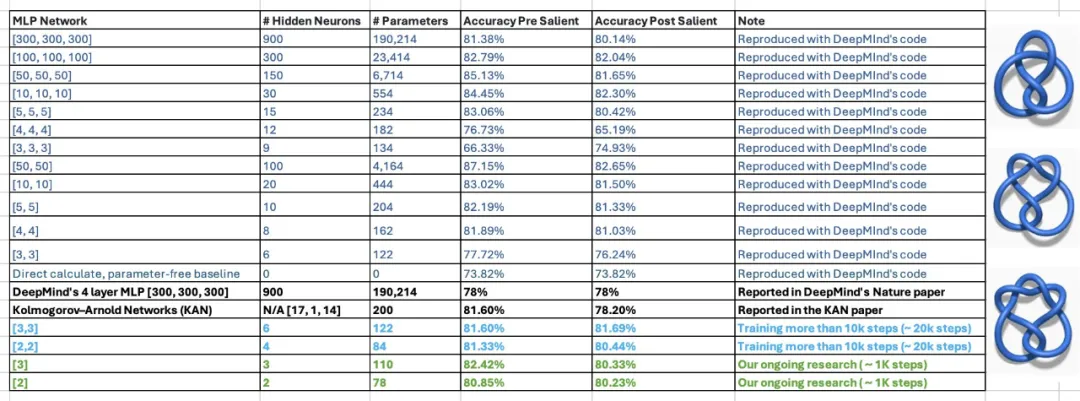
对此，论文作者也给出了积极的回应：
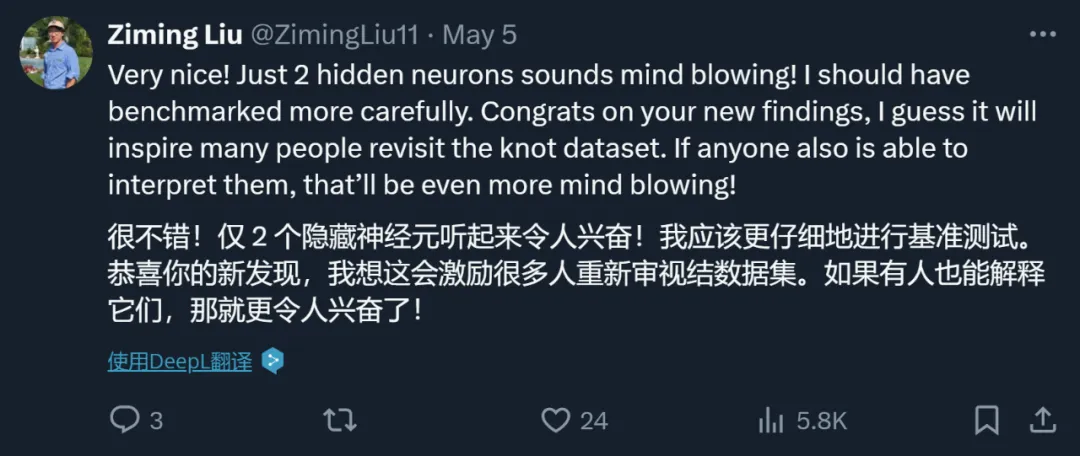
第二，KAN 和 MLP 从方法上没有本质不同。
「是的，这显然是一回事。他们在 KAN 中先做激活，然后再做线性组合，而在 MLP 中先做线性组合，然后再做激活。将其放大，基本上就是一回事。据我所知，使用 KAN 的主要原因是可解释性和符号回归。」
除了对方法的质疑之外，研究者还呼吁对这篇论文的评价回归理性：
「我认为人们需要停止将 KAN 论文视为深度学习基本单元的巨大转变，而只是将其视为一篇关于深度学习可解释性的好论文。在每条边上学习到的非线性函数的可解释性是这篇论文的主要贡献。」
第三，有研究者表示，KAN 的思路并不新奇。
「人们在 20 世纪 80 年代对此进行了研究。Hacker News 的讨论中提到了一篇意大利论文讨论过这个问题。所以这根本不是什么新鲜事。40 年过去了，这只是一些要么回来了，要么被拒绝的东西被重新审视的东西。」
但可以看到的是，KAN 论文的作者也没有掩盖这一问题。
「这些想法并不新鲜，但我不认为作者回避了这一点。他只是把所有东西都很好地打包起来，并对 toy 数据进行了一些很好的实验。但这也是一种贡献。」
与此同时，Ian Goodfellow、Yoshua Bengio 十多年前的论文 MaxOut（https://arxiv.org/pdf/1302.4389）也被提到，一些研究者认为二者「虽然略有不同，但想法有点相似」。
作者：最初研究目标确实是可解释性
热烈讨论的结果就是，作者之一 Sachin Vaidya 站出来了。
作为该论文的作者之一，我想说几句。KAN 受到的关注令人惊叹，而这种讨论正是将新技术推向极限、找出哪些可行或不可行所需要的。
我想我应该分享一些关于动机的背景资料。我们实现 KAN 的主要想法源于我们正在寻找可解释的人工智能模型，这种模型可以「学习」物理学家发现自然规律的洞察力。因此，正如其他人所意识到的那样，我们完全专注于这一目标，因为传统的黑箱模型无法提供对科学基础发现至关重要的见解。然后，我们通过与物理学和数学相关的例子表明，KAN 在可解释性方面大大优于传统方法。我们当然希望，KAN 的实用性将远远超出我们最初的动机。
在 GitHub 主页中，论文作者之一刘子鸣也对这项研究受到的评价进行了回应：
最近我被问到的最常见的问题是 KAN 是否会成为下一代 LLM。我对此没有很清楚的判断。
KAN 专为关心高精度和可解释性的应用程序而设计。我们确实关心 LLM 的可解释性，但可解释性对于 LLM 和科学来说可能意味着截然不同的事情。我们关心 LLM 的高精度吗？缩放定律似乎意味着如此，但可能精度不太高。此外，对于 LLM 和科学来说，准确性也可能意味着不同的事情。
我欢迎人们批评 KAN，实践是检验真理的唯一标准。很多事情我们事先并不知道，直到它们经过真正的尝试并被证明是成功还是失败。尽管我愿意看到 KAN 的成功，但我同样对 KAN 的失败感到好奇。
KAN 和 MLP 不能相互替代，它们在某些情况下各有优势，在某些情况下各有局限性。我会对包含两者的理论框架感兴趣，甚至可以提出新的替代方案（物理学家喜欢统一理论，抱歉）。
KAN 论文一作刘子鸣。他是一名物理学家和机器学习研究员，目前是麻省理工学院和 IAIFI 的三年级博士生，导师是 Max Tegmark。他的研究兴趣主要集中在人工智能 AI 和物理的交叉领域。
