JavaScript数据结构与算法之栈详解_javascript技巧
在上一篇博客介绍了下列表,列表是最简单的一种结构,但是如果要处理一些比较复杂的结构,列表显得太简陋了,所以我们需要某种和列表类似但是更复杂的数据结构---栈。栈是一种高效的数据结构,因为数据只能在栈顶添加或删除,所以这样操作很快,而且容易实现。
一:对栈的操作。
栈是一种特殊的列表,栈内的元素只能通过列表的一端访问,这一端陈为栈顶。比如餐馆里面洗盘子,只能先洗最上面的盘子,盘子洗完后,也只能螺到这一摞盘子的最上面。栈被称为 "后入先出"(LIFO)的数据结构。
由于栈具有后入先出的特点,所以任何不在栈顶的元素都无法访问,为了得到栈低的元素,必须先拿掉上面的元素。我们可以对栈的两种主要操作是将一个元素 压入栈 和 将一个元素 弹出栈。入栈我们可以使用方法push()方法,出栈我们使用pop()方法。pop()方法虽然可以访问栈顶的元素,但是调用该方法后,栈顶元素也就从栈中被永久性的删除了。另一个我们很常用的方法是peek(),该方法只返回栈顶元素,而不删除它。
入栈和出栈的实列图如下:
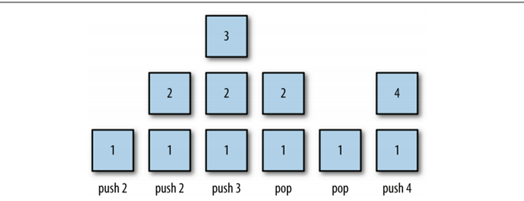
push(),pop()和peek()是栈的三个主要方法,但是栈还有其他方法和属性。如下:
clear():清除栈内的所有元素。
length(): 记录栈内元素的个数。
二:对栈的实现如下:
我们可以先实现栈类的方法开始;如下:
function Stack() {
this.dataStore = [];
this.top = 0;
}
如上:dataStore 是保存栈内的所有元素。变量top记录栈顶的位置,初始化为0. 表示栈顶对应数组的起始位置为0,如果有元素被压入栈。该变量值将随之变化。
我们还有如下几个方法:push(), pop(), peek(),clear(),length();
1. push()方法;当向栈内压入一个新元素时,需要将其保存在数组中变量top所对应的位置,然后top值加1,让其指向数组中下一个位置。如下代码:
function push(element) {
this.dataStore[this.top++] = element;
}
2. pop()方法与push()方法相反---它返回栈顶元素,同时将top值减1.如下代码:
function pop(){
return this.dataStore[--this.top];
}
3. peek()方法返回数组的第top-1个位置的元素,即栈顶元素;
function peek(){
return this.dataStore[this.top - 1];
}
4. length()方法 有时候我们要知道栈内有多少个元素,我们可以通过返回变量top值的方式返回栈内的元素个数,如下代码:
function length(){
return this.top;
}
5. clear(); 有时候我们要清空栈,我们将变量top值设为0;如下代码:
function clear() {
this.top = 0;
}
如下所有代码:
function Stack() {
this.dataStore = [];
this.top = 0;
}
Stack.prototype = {
// 向栈中压入一个新元素
push: function(element) {
this.dataStore[this.top++] = element;
},
// 访问栈顶元素,栈顶元素永久的被删除了
pop: function(){
return this.dataStore[--this.top];
},
// 返回数组中的 top-1 个位置的元素,即栈顶元素
peek: function(){
return this.dataStore[this.top - 1];
},
// 栈内存储了多少个元素
length: function(){
return this.top;
},
// 清空栈
clear: function(){
this.top = 0;
}
};
demo实例如下:
var stack = new Stack();
stack.push("a");
stack.push("b");
stack.push("c");
console.log(stack.length()); // 3
console.log(stack.peek()); // c
var popped = stack.pop();
console.log(popped); // c
console.log(stack.peek()); // b
stack.push("d");
console.log(stack.peek()); // d
stack.clear();
console.log(stack.length()); // 0
console.log(stack.peek()); // undefined
下面我们可以实现一个阶乘函数的递归定义;比如5!的阶乘 5!= 5 * 4 * 3 * 2 * 1;
如下代码:
function fact(n) {
var s = new Stack();
while(n > 1) {
s.push(n--);
}
var product = 1;
while(s.length() > 0) {
product *= s.pop();
}
return product;
}
console.log(fact(5));
上面的代码含义是:先数字5传入函数,使用while循环,每次自减1的之前,把自己使用栈的函数push()压入栈内,直到变量n 小于 1为止。然后定义一个变量product;通过栈的length()的方法判断是否大于0 且每次执行 product* = s.pop(); pop()方法返回栈顶元素,且从栈中删掉该元素。所以每次执行一次,就删掉一个元素,直到s.length()

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)
 使用C++实现机器学习算法:常见挑战及解决方案
Jun 03, 2024 pm 01:25 PM
使用C++实现机器学习算法:常见挑战及解决方案
Jun 03, 2024 pm 01:25 PM
C++中机器学习算法面临的常见挑战包括内存管理、多线程、性能优化和可维护性。解决方案包括使用智能指针、现代线程库、SIMD指令和第三方库,并遵循代码风格指南和使用自动化工具。实践案例展示了如何利用Eigen库实现线性回归算法,有效地管理内存和使用高性能矩阵操作。
 探究C++sort函数的底层原理与算法选择
Apr 02, 2024 pm 05:36 PM
探究C++sort函数的底层原理与算法选择
Apr 02, 2024 pm 05:36 PM
C++sort函数底层采用归并排序,其复杂度为O(nlogn),并提供不同的排序算法选择,包括快速排序、堆排序和稳定排序。
 使用Java函数比较进行复杂数据结构比较
Apr 19, 2024 pm 10:24 PM
使用Java函数比较进行复杂数据结构比较
Apr 19, 2024 pm 10:24 PM
Java中比较复杂数据结构时,使用Comparator提供灵活的比较机制。具体步骤包括:定义比较器类,重写compare方法定义比较逻辑。创建比较器实例。使用Collections.sort方法,传入集合和比较器实例。
 改进的检测算法:用于高分辨率光学遥感图像目标检测
Jun 06, 2024 pm 12:33 PM
改进的检测算法:用于高分辨率光学遥感图像目标检测
Jun 06, 2024 pm 12:33 PM
01前景概要目前,难以在检测效率和检测结果之间取得适当的平衡。我们就研究出了一种用于高分辨率光学遥感图像中目标检测的增强YOLOv5算法,利用多层特征金字塔、多检测头策略和混合注意力模块来提高光学遥感图像的目标检测网络的效果。根据SIMD数据集,新算法的mAP比YOLOv5好2.2%,比YOLOX好8.48%,在检测结果和速度之间实现了更好的平衡。02背景&动机随着远感技术的快速发展,高分辨率光学远感图像已被用于描述地球表面的许多物体,包括飞机、汽车、建筑物等。目标检测在远感图像的解释中
 算法在 58 画像平台建设中的应用
May 09, 2024 am 09:01 AM
算法在 58 画像平台建设中的应用
May 09, 2024 am 09:01 AM
一、58画像平台建设背景首先和大家分享下58画像平台的建设背景。1.传统的画像平台传统的思路已经不够,建设用户画像平台依赖数据仓库建模能力,整合多业务线数据,构建准确的用户画像;还需要数据挖掘,理解用户行为、兴趣和需求,提供算法侧的能力;最后,还需要具备数据平台能力,高效存储、查询和共享用户画像数据,提供画像服务。业务自建画像平台和中台类型画像平台主要区别在于,业务自建画像平台服务单条业务线,按需定制;中台平台服务多条业务线,建模复杂,提供更为通用的能力。2.58中台画像建设的背景58的用户画像
 Java数据结构与算法:深入详解
May 08, 2024 pm 10:12 PM
Java数据结构与算法:深入详解
May 08, 2024 pm 10:12 PM
数据结构和算法是Java开发的基础,本文深入探讨Java中的关键数据结构(如数组、链表、树等)和算法(如排序、搜索、图算法等)。这些结构通过实战案例进行说明,包括使用数组存储分数、使用链表管理购物清单、使用栈实现递归、使用队列同步线程以及使用树和哈希表进行快速搜索和身份验证等。理解这些概念可以编写高效且可维护的Java代码。
 PHP数据结构:AVL树的平衡之道,维持高效有序的数据结构
Jun 03, 2024 am 09:58 AM
PHP数据结构:AVL树的平衡之道,维持高效有序的数据结构
Jun 03, 2024 am 09:58 AM
AVL树是一种平衡二叉搜索树,确保快速高效的数据操作。为了实现平衡,它执行左旋和右旋操作,调整违反平衡的子树。AVL树利用高度平衡,确保树的高度相对于节点数始终较小,从而实现对数时间复杂度(O(logn))的查找操作,即使在大型数据集上也能保持数据结构的效率。
 开创性CVM算法破解40多年计数难题!计算机科学家掷硬币算出「哈姆雷特」独特单词
Jun 07, 2024 pm 03:44 PM
开创性CVM算法破解40多年计数难题!计算机科学家掷硬币算出「哈姆雷特」独特单词
Jun 07, 2024 pm 03:44 PM
计数,听起来简单,却在实际执行很有难度。想象一下,你被送到一片原始热带雨林,进行野生动物普查。每当看到一只动物,拍一张照片。数码相机只是记录追踪动物总数,但你对独特动物的数量感兴趣,却没有统计。那么,若想获取这一独特动物数量,最好的方法是什么?这时,你一定会说,从现在开始计数,最后再从照片中将每一种新物种与名单进行比较。然而,这种常见的计数方法,有时并不适用于高达数十亿条目的信息量。来自印度统计研究所、UNL、新加坡国立大学的计算机科学家提出了一种新算法——CVM。它可以近似计算长列表中,不同条






