遇到一道笔试题,完全没思路,求助。。。。
已知类定义如下
class Node {
public Double value;
public List<Node> children;
}输入node满足以下条件:
1 node的value是大于0的浮点数
2 node的下级节点(以及更下级节点)的value可能是null或者大于0的浮点数
程序的作用如下:
1 将树形结构里面所有value是null的均设为大于0的浮点数
2 非叶子节点(即children数量大于0的节点)的value均等于它的children的value之和
public void doit(Node node){
......
}示例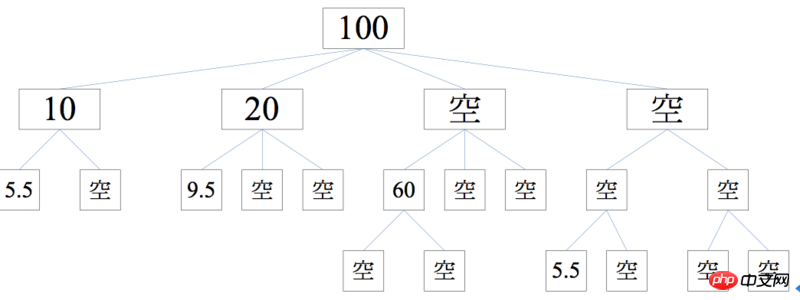
解答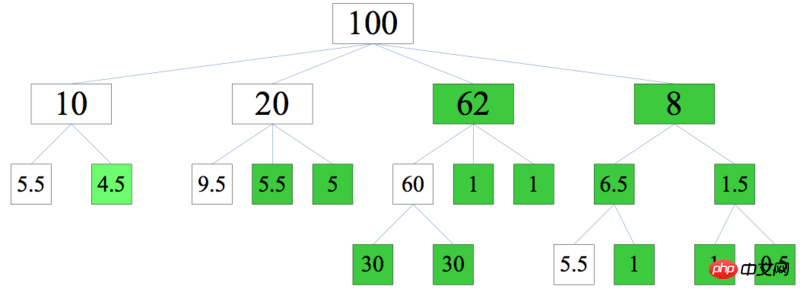
这个问题要如何解答?
已经有高手答出来了,综合一下下面两人的答案就是完美答案。其实就是我采纳那个答案里面把均分改为随机就很完美了
没有写具体代码,说一下思路吧
首先,把问题分为2步
Step1、确定非叶子节点的值
Step2、确定叶子节点的值
先处理Step1,处理完Step1之后,Step2就不用多说了,根据父节点的值均分即可。
对于Step1,
step1-1: 由下向上遍历各个非叶子节点,通过对其子节点求和,确定其最小值。如最右侧的子树,最小值为5.5。
step1-2: 由上向下,逐层确定非叶子节点,为方面描述,命名[100]为第一层,[10,20,?,?]为第二层,以此类推。根据step1-1的结果,第二层的最小值为[10,20,>60,>5.5],将100减去最小值之和,然后均分,结果为[10,20,62.25,7.75]
step1-3: 同上,确定第三层,结果为[5.5, 4.5] [9.5, 5.25, 5.25] [60, 1.125, 1.125] [6.625,1.125]
这里最后一组较特别,需要考虑到7.75分配的时候,其左下已经有5.5了,所以7.75里面可自由支配的数为7.75-5.5=2.25,将2.25均分到两边,结果[6.625,1.125]
step1-4: 最后一层相信不用再罗嗦了,其实就是step2,均分下来就好。
刚刚看了一下这道题目,觉得很有意思。然后思考了一下,提出以下问题。
我的思路的话就是递归。
分层次遍历,在每层的时候把确定的值加起来,为空的节点们去分父节点的值减去这部分确定的值的和(题目的要求)。然后如果不是叶节点的节点按照上述方法递归。
但是确定每个节点的值得时候,如某些叶子节点的时候,我们需要随机给他们赋值,他们的值有些受到父节点约束,有些不收父节点约束比如第二层的第三个节点的两个叶子节点,如果我们赋给他们的值使得他们的父节点不满足要求了,这就不符合题意了。所以我想的是在每次确定值得时候传入这些节点的取值范围。这些范围的确定又会导致一些问题,问题又会变得复杂。
范围确定,每个空节点的最大值肯定是父节点的值减去同行子节点的值的和,最小取值肯定是大于其子节点的有值元素的和。因为只有确定了某个范围,其叶子节点的一些随机值的取法不会导致其余节点不符合题意。总的意思来说每个同父节点的空节点的取值互相有约束,其中一个节点的取值虽然满足自身,但是会使得其余节点不满足要求。举个例子:

如果这样取值,则局部满足,会导致其他节点的取值不满足要求。所以在没约束的情况下可能会导致意想不到的结果。我们需要去确定这些范围。
综上,这只是我的一些思考后的一些想法,也许有错误的地方欢迎指正。