递归算法的时间复杂度是:【T(n)=o(f(n))】,它表示随问题规模n的增大,算法的执行时间增长率和f(n)增长率成正比,这称作算法的渐进时间复杂度。

递归算法的时间复杂度
时间复杂度:
一般情况下,算法中基本操作重复的次数就是问题规模n的某个函数f(n),进而分析f(n)随n的变化情况并确定T(n)的数量级。这里用‘o’来表示数量级,给出算法时间复杂度。
T(n)=o(f(n));
它表示随问题规模n的增大,算法的执行时间增长率和f(n)增长率成正比,这称作算法的渐进时间复杂度。而我们一般情况下讨论的最坏的时间复杂度。
推荐课程:C语言教程
空间复杂度:
算法的空间复杂度并不是实际占用的空间,而是计算整个算法空间辅助空间单元的个数,与问题的规模没有关系。算法的空间复杂度S(n)定义为该算法所耗费空间的数量级。
S(n)=o(f(n))
若算法执行所需要的辅助空间相对于输入数据n而言是一个常数,则称这个算法空间复杂度辅助空间为o(1);
递归算法空间复杂度:递归深度n*每次递归所要的辅助空间,如果每次递归所需要的辅助空间为常数,则递归空间复杂度o(n)。
递归算法时间复杂度的计算方程式是一个递归方程:
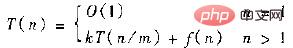
在引入递归树之前可以考虑一个例子:
T(n) = 2T(n/2) + n2
迭代2次可以得:
T(n) = n2 + 2(2T(n/4) + (n/2) 2)
还可以继续迭代,将其完全展开可得:
T(n) = n2 + 2((n/2) 2 + 2((n/22)2 + 2((n/23) 2 + 2((n/24) 2 +…+2((n/2i) 2 + 2T(n/2i + 1)))…))))……(1)
而当n/2i+1 == 1时,迭代结束。
将(1)式小括号展开,可得:
T(n) = n2 + 2(n/2)2 + 22(n/22) 2 + … + 2i(n/2i)2 + 2i+1T(n/2i+1)
这恰好是一个树形结构,由此可引出递归树法。
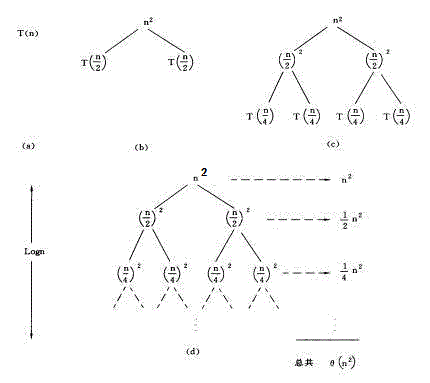
图中的(a)(b)(c)(d)分别是递归树生成的第1,2,3,n步。每一节点中都将当前的自由项n2留在其中,而将两个递归项T(n/2)
+ T(n/2)分别摊给了他的两个子节点,如此循环。
图中所有节点之和为:
[1 + 1/2 + (1/2)2 + (1/2)3 + … + (1/2)i] n2 = 2n2
可知其时间复杂度为O(n2)
可以得到递归树的规则为:
(1)每层的节点为T(n) = kT(n / m) + f(n)中的f(n)在当前的n/m下的值;
(2)每个节点的分支数为k;
(3)每层的右侧标出当前层中所有节点的和。
再举个例子:
T(n) = T(n/3) + T(2n/3) + n
其递归树如下图所示:
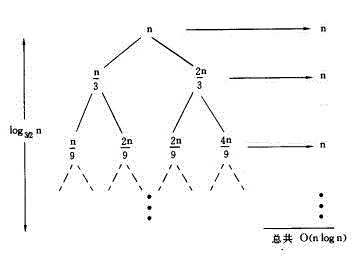
可见每层的值都为n,从根到叶节点的最长路径是:
因为最后递归的停止是在(2/3)kn == 1.则
于是
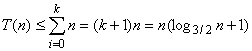
即T(n) = O(nlogn)
总结,利用此方法解递归算法复杂度:
f(n) = af(n/b) + d(n)
1.当d(n)为常数时:
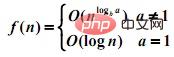
2.当d(n) = cn 时:
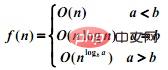
3.当d(n)为其他情况时可用递归树进行分析。
由第二种情况知,若采用分治法对原算法进行改进,则着重点是采用新的计算方法缩小a值。
以上就是递归算法的时间复杂度是什么的详细内容,更多请关注php中文网其它相关文章!

每个人都需要一台速度更快、更稳定的 PC。随着时间的推移,垃圾文件、旧注册表数据和不必要的后台进程会占用资源并降低性能。幸运的是,许多工具可以让 Windows 保持平稳运行。

Copyright 2014-2025 https://www.php.cn/ All Rights Reserved | php.cn | 湘ICP备2023035733号