在 2023 年举行的国际学术会议 AIBT 2023 上,Ratidar Technologies LLC 发表了一篇基于公平性的排序学习算法,并荣获该会议的最佳论文报告奖。该算法名为斯奇拉姆排序 (Skellam Rank),充分利用了统计学原理,结合了Pairwise Ranking和矩阵分解技术,以解决推荐系统中的准确率和公平性问题。由于推荐系统中创新的排序学习算法很少,斯奇拉姆排序算法表现出色,因此在会议上获得了研究奖项。下面将介绍斯奇拉姆算法的基本原理:
我们首先回忆一下泊松分布:
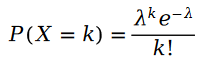
泊松分布的参数 的计算公式如下:
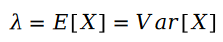
两个泊松变量的差值是斯奇拉姆分布:
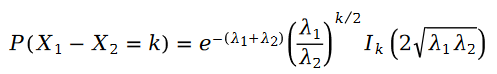
在公式中,我们有:
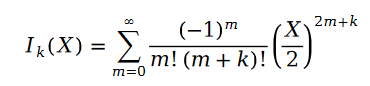
函数 叫做第一类贝塞尔函数。
有了这些最基本的统计学中的概念,下面让我们来构建一个 Pairwise Ranking 的排序学习推荐系统吧!
我们首先认为用户给物品的打分是个泊松分布的概念。也就是说,用户物品评分值服从以下概率分布:
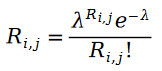
之所以我们可以把用户给物品打分的过程描述为泊松过程,是因为用户物品评分存在马太效应,也就是说评分越高的用户,打分的人越多,以至于我们可以用某个物品的评分的人的数量来近似该物品的评分的分布。给某个物品打分的人数服从什么随机过程呢?自然而然的,我们就会想到泊松过程。因为用户给物品打分的概率和该物品有多少人打分的概率相近,我们自然也就可以用泊松过程来近似用户给物品打分的这一过程了。
我们下面把泊松过程的参数用样本数据的统计量替代,得到下面的公式:
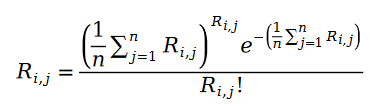
我们下面定义 Pariwise Ranking 的最大似然函数公式。众所周知,所谓 Pairwise Ranking 指的是我们利用最大似然函数求解模型参数,使得模型能够最大程度保持数据样本中已知的排序对的关系:
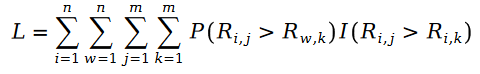
因为公式中的 R 是泊松分布,所以它们的差值,就是斯奇拉姆分布,也就是说:
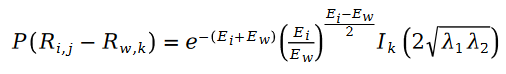
其中变量 E 是按照如下方式定义的:
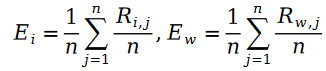
我们把斯奇拉姆分布的公式带入最大似然函数的损失函数 L ,得到了如下公式:
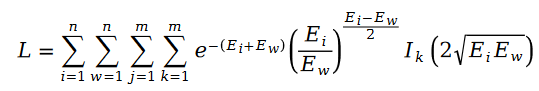
在变量 E 中出现的用户评分值 R ,我们利用矩阵分解的方式进行求解。将矩阵分解中的参数用户特征向量 U 和物品特征向量 V 作为待求解变量:
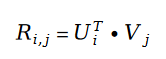
这里我们先回顾一下矩阵分解的概念。矩阵分解的概念是在 2010 年左右的时候提出的推荐系统算法,该算法可以说是历史上最成功的推荐系统算法之一。时至今日,仍然有大量的推荐系统公司利用矩阵分解算法作为线上系统的 baseline,而时下大热的经典推荐算法 DeepFM 中的重要组件 Factorization Machine,也是推荐系统算法中的矩阵分解算法后续的改进版本,和矩阵分解有千丝万缕的联系。矩阵分解算法有个里程碑论文,是 2007 年的 Probabilistic Matrix Factorization,作者利用统计学习模型对矩阵分解这个线性代数中的概念重新建模,使得矩阵分解第一次有了扎实的数学理论基础。
矩阵分解的基本概念,是利用向量的点乘,在对用户评分矩阵进行降维的同时高效的预测未知的用户评分。矩阵分解的损失函数如下:
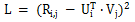
矩阵分解算法有许多的变种,比如上海交大提出的 SVDFeature,把向量 U 和 V 用线性组合的形式进行建模,使得矩阵分解的问题变成了特征工程的问题。SVDFeature 也是矩阵分解领域的里程碑论文。矩阵分解可以被应用在 Pairwise Ranking 中用以取代未知的用户评分,从而达到建模的目的,经典的应用案例包括 Bayesian Pairwise Ranking 中的 BPR-MF 算法,而斯奇拉姆排序算法就是借鉴了同样的思路。
我们用随机梯度下降对斯奇拉姆排序算法进行求解。因为随机梯度下降在求解过程中,可以对损失函数进行大量的简化从而达到求解的目的,我们的损失函数变成了下面的公式:
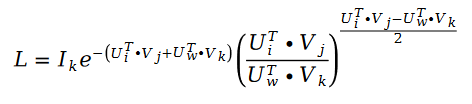
利用随机梯度下降对未知参数 U 和 V 进行求解,我们得到了迭代公式如下:
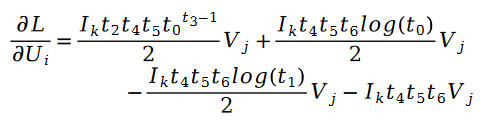
其中:
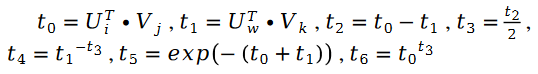
另外有:
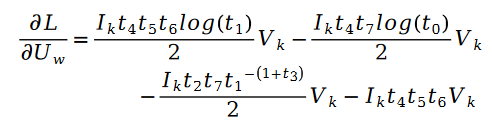
其中:
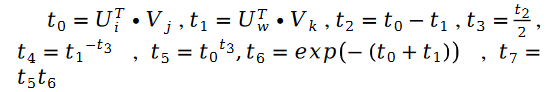
对于未知参数变量 V 的求解类似,我们有如下公式:
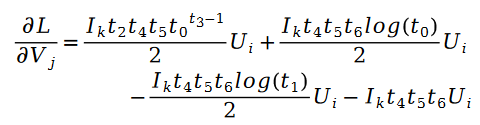
其中:
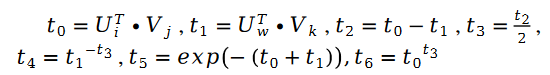
另外有:
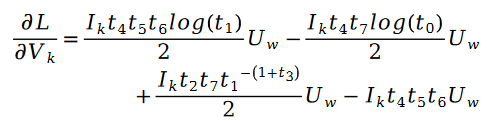
其中:
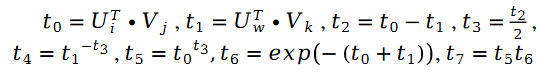
整个算法的流程,我们用如下的伪代码进行展示:

为了验证算法的有效性,论文作者在 MovieLens 1 Million Dataset 和 LDOS-CoMoDa Dataset 上进行了测试。第一个数据集包含了 6040 个用户和 3706 部电影的评分,整个评分数据集大概有 100 万评分数据,是推荐系统领域最知名的评分数据集合之一。第二个数据集合来自斯洛文尼亚,是网上不多见的基于场景的推荐系统数据集合。该数据集合包含了 121 个用户和 1232 部电影的评分。作者将斯奇拉姆排序和另外 9 种推荐系统算法进行了对比,主要测评指标为 MAE (Mean Absolute Error,用来测试准确性)和 Degree of Matthew Effect (主要用来测试公平性):
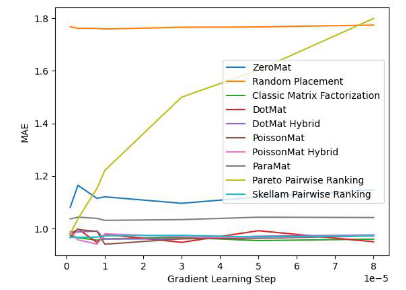
图 1. MovieLens 1 Million Dataset (MAE 指标)
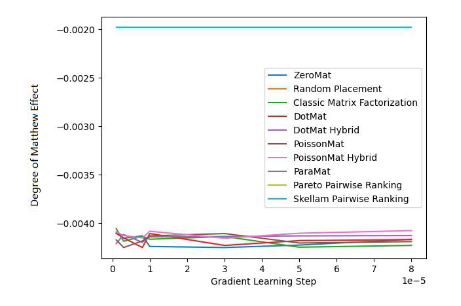
图 2. MovieLens 1 Million Dataset (Degree of Matthew Effect 指标)
通过图 1 和图 2 ,我们发现斯奇拉姆排序在 MAE 这一项指标上表现优异,但在 Grid Search 的整个实验过程中,无法一直保证性能优于其他算法。但是在图 2 中,我们发现斯奇拉姆排序在公平性指标上一骑绝尘,遥遥领先于另外 9 种推荐系统算法。
下面我们看一下该算法在 LDOS-CoMoDa 数据集合上的表现:
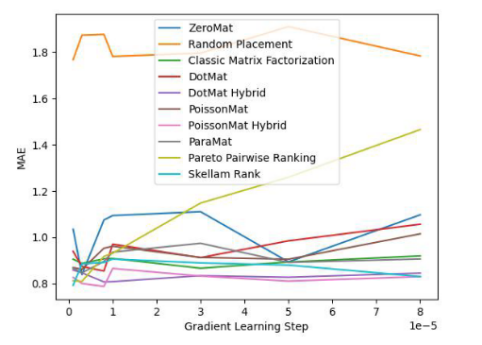
图 3. LDOS-CoMoDa Dataset (MAE 指标)
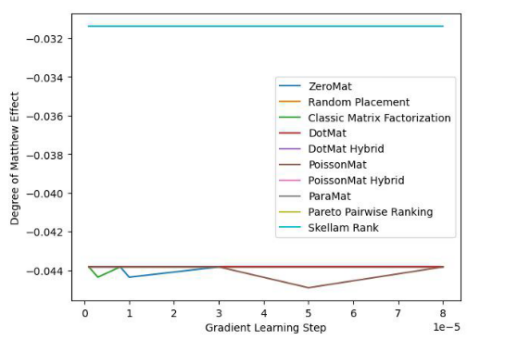
图 4. LDOS-CoMoDa Dataset (Degree of Matthew Effect 指标)
通过图3和图4,我们了解到斯奇拉姆排序在公平性指标上一骑绝尘,在准确性指标上表现优异。结论和上一个实验类似。
斯奇拉姆排序结合了泊松分布、矩阵分解和 Pairwise Ranking 等概念,是一个不可多得的推荐系统排序学习算法。在技术领域,掌握排序学习技术的人只占掌握深度学习的人的人数的1/6,因此排序学习属于稀缺技术。而能够在推荐系统领域发明原创性排序学习的人才更是少之又少。排序学习算法,把人们从评分预测的狭隘视角中解放了出来,让人们意识到最重要的事情是顺序,而不是分值。基于公平性的排序学习,目前在信息检索领域中大火,特别是 SIGIR 等顶会,非常欢迎基于公平性的推荐系统的论文,希望能够得到读者们的关注。
汪昊,前 Funplus 人工智能实验室负责人。曾在 ThoughtWorks、豆瓣、百度、新浪等公司担任技术和技术高管职务。在互联网公司和金融科技、游戏等公司任职 12 年,对于人工智能、计算机图形学和区块链等领域有着深刻的见解和丰富的经验。在国际学术会议和期刊发表论文 42 篇,获得IEEE SMI 2008 最佳论文奖、ICBDT 2020 / IEEE ICISCAE 2021 / AIBT 2023 最佳论文报告奖。
以上就是斯奇拉姆排序 - 基于公平性的排序学习的详细内容,更多请关注php中文网其它相关文章!

每个人都需要一台速度更快、更稳定的 PC。随着时间的推移,垃圾文件、旧注册表数据和不必要的后台进程会占用资源并降低性能。幸运的是,许多工具可以让 Windows 保持平稳运行。

Copyright 2014-2025 https://www.php.cn/ All Rights Reserved | php.cn | 湘ICP备2023035733号