求素数的方法:1、遍历1~n区间中的所有自然数给n来除,若余数为0则表示该数n不是素数,否则就是素数,语法“for(i=2;i

本教程操作环境:windows7系统、javascript1.8.5版、Dell G3电脑。
素数又叫质数,素数是指在大于1的自然数中,除了1和它本身以外,不能被其他自然数整除的数。
100以内的素数:2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97,共计25个。
素数只能被1和自身整除,所以遍历(1,n)开区间中的所有自然数给n来除,若存在整除,即余数为0,则表示该数n不是素数,否则就是素数。
立即学习“Java免费学习笔记(深入)”;
function isPrime(n) {
n = parseInt(n);
if (n <= 3) {
return n > 1;
}
for (let i = 2; i < n; i++) {
if (n % i === 0) {
return false;
}
}
return true;
}但是这种算法的复杂度为O(n)
假设n不是素数,则n除了可以被1和n整除外,还可以被i、j整除,即 n / i = j...0,比如15不是素数,15 / 3 = 5,比如35不是素数,35 / 5 = 7,此时i,j必然分别处于(1, Math.sqrt(n)]和[Math.sqrt(n), n) 之中,比如Math.sqrt(15) ≈ 3.8,则 3处于(1,3.8],5处于[3.8, 15)。比如Math.sqrt(4) = 2,则2处于(1,2]中,也处于[2,4)中。
function isPrime(n) {
n = parseInt(n);
if (n <= 3) {
return n > 1;
}
for (let i = 2; i <= Math.sqrt(n); i++) {
if (n % i === 0) {
return false;
}
}
return true;
}此时算法复杂度为O(sqrt(n))
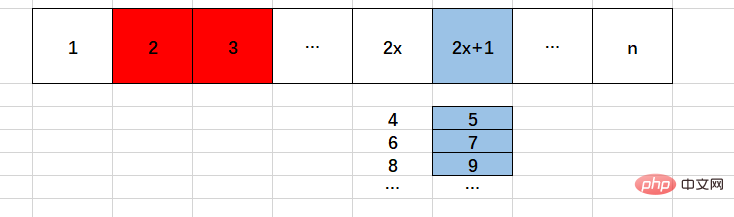
除了2,所有偶数都不是素数
function isPrime(n) {
n = parseInt(n);
if (n <= 3) {
return n > 1;
}
if (n % 2 === 0) {
return false;
}
for (let i = 3; i <= Math.sqrt(n); i += 2) {
if (n % i === 0) {
return false;
}
}
return true;
}for循环中n,只能为上图浅蓝色部分。
因此上面算法减少了一半的循环,时间复杂度为O(sqrt(n) / 2)
需要注意的是,本算法的代码不能将n % 2 === 0 的判断条件加入到循环中,如下代码存在漏洞
function isPrime(n) {
n = parseInt(n);
if (n <= 3) {
return n > 1;
}
for (let i = 3; i <= Math.sqrt(n); i += 2) {
if (n % 2 === 0 || n % i === 0) {
return false;
}
}
return true;
}此时4、6、8都会被判定为素数。
漏洞形成的原因是,for循环的循环条件 i
该算法只能保证循环条件 i = i^2 = 9 时。
大于等于5的素数一定和6的倍数相邻
(注意这句话不等价于:和6的倍数相邻的数一定是大于5的素数,该结论不成立。)
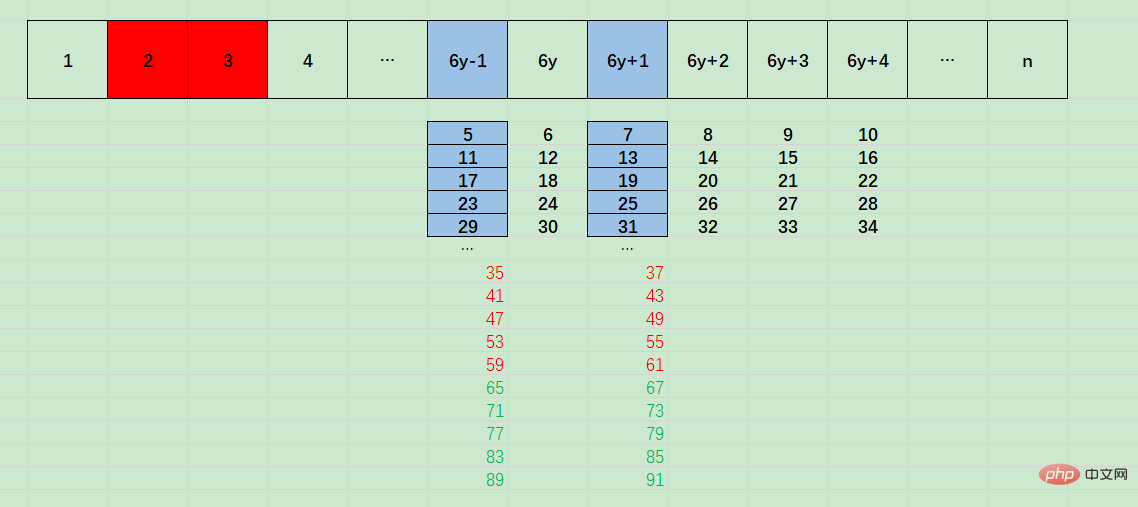
如上图中,将大于等于5的数分为了:6y-1、6y、6y+1、6y+2、6y+3、6y+4(y>=1)
其中,6y、6y+2、6y+3、6y+4都不可能是素数,只有6y-1和6y+1可能是素数。
另外,6y-1(y>=1)和 6y + 5 (y>=0)等价。
所以,我们可以将n不为6y-1(或6y+5)和6y+1的数直接排除,排除方法为,
if (n % 6 !== 1 && n % 6 !== 5) {
return false;
}下面要剔除掉6y-1(或6y+5)和6y+1中的非素数,
for (let i = 5; i <= Math.sqrt(n); i += 6) {
if (n % i === 0 || n % (i + 2) === 0) {
return false;
}
}这里大家比较疑惑的可能有两点:
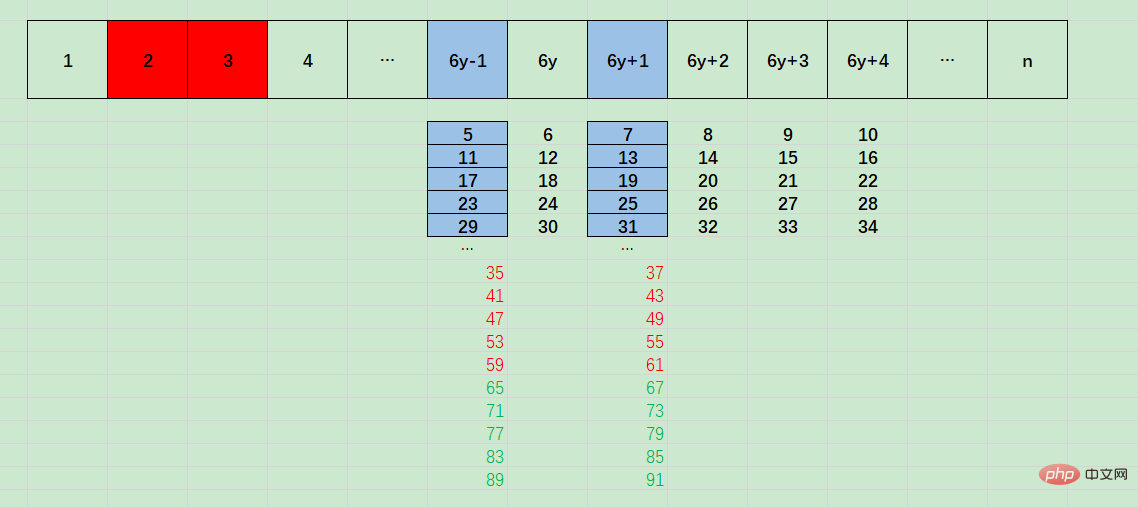
我们看上面图解,可以发现,6y-1,是基数为5,差值为6的等差数列,即 5 + 6x :
6y+1,是基数为7,差值为6的等差数列,即 7 + 6x :
所以6y-1和6y+1可能整除的数自增量为6,这是for循环i自增为啥是 6的原因
且6y-1和6y+1的整除数基数为5和7,相差为2,这是for循环中素数判定的条件为啥是 n % i === 0 || n % (i+2) === 0的原因
function isPrime(n) {
n = parseInt(n);
if (n <= 3) {
return n > 1;
}
if (n % 6 !== 1 && n % 6 !== 5) {
return false;
}
for (let i = 5; i <= Math.sqrt(n); i += 6) {
if (n % i === 0 || n % (i + 2) === 0) {
return false;
}
}
return true;
}此时时间复杂度为 O(sqrt(n) / 3)
【相关推荐:javascript视频教程、编程基础视频】
以上就是javascript怎么求素数的详细内容,更多请关注php中文网其它相关文章!

java怎么学习?java怎么入门?java在哪学?java怎么学才快?不用担心,这里为大家提供了java速学教程(入门到精通),有需要的小伙伴保存下载就能学习啦!




Copyright 2014-2025 https://www.php.cn/ All Rights Reserved | php.cn | 湘ICP备2023035733号